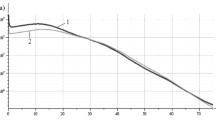
A model of nonstationary motion of a gas–liquid mixture in a bed–pipeline system, with a new source included in the main line has been constructed taking into account heat transfer between a gas–liquid mixture flow in a rising pipe and the medium around the flow, and solutions to boundary-value problems are given. In the first approximation, the influence of a change in the rheological properties of the gas–liquid mixture with temperature on the dynamics of its motion is determined. Analytical formulas have been obtained making it possible to determine the dynamics of pressure at the bottom of the well and the productivity of the bed depending on the parameters of the system. Numerical calculations are carried out at practical values of the system parameters.
Similar content being viewed by others
References
L. S. Leibenson, Underground Hydrodynamics, Collected works [in Russian], Vol. II, Izd. Akad. Nauk SSSR, Moscow (1953).
S. M. Targ, Basic Problems of the Theory of Laminar Flows [in Russian], Gos. Izd. Tekhn.-Teor. Lit., Moscow (1951).
É. B. Chekalyuk, Thermodynamics of the Oil Bed [in Russian], Nedra, Moscow (1965).
L. I. Rubinshtein, Temperature Fields in Oil Beds [in Russian], Nauka, Moscow (1972).
Yu. S. Teplitskii, Heat exchange in a tube filled with granular bed, J. Eng. Phys. Thermophys., 77, No. 1, 103–110 (2004).
É. M. Abbasov, T. S. Kengerli, and N. R. Abdullaeva, Simulation of the process of filtration of a gas–liquid mixture in the bed–well conjugate system, J. Eng. Phys. Thermophys., 93, No. 5, 1147–1155 (2020).
É. M. Abbasov and S. A. Imamaliev, Mathematical simulation of unsteady-state gas–liquid mixture flow in a bed–well system, J. Eng. Phys. Thermophys., 89, No. 5, 1111–1122 (2016).
Y. Zhou, Parallel General-Purpose Reservoir Simulation with Coupled Reservoir Models and Multisegment Wells, PhD Thesis, Stanford (2012).
Y. Jiang, Techniques for Modeling Complex Reservoirs and Advanced Wells, PhD Thesis, Stanford (2007).
D. W. Peaceman, Interpretation of well-block pressures in numerical reservoir simulation with nonsquare grid blocks and anisotropic permeability, in: Proc. SPE Symp. on Reservoir Simulation, 31 June–3 February, New Orleans (1982).
R. M. Sitdikov, D. D. Filippov, and D. A. Mitrushkin, Numerical Simulation of Multiphase Flows in the "Bed–Well–UEChN" Conjugate System, Preprint of the M. V. Keldysh Institute of Applied Mathematics, Moscow (2016).
V. A. Galkin, D. A. Bykovskikh, T. V. Gavrilenko, and P. A. Stulov, The filtration model of an ideal gas in a porous medium, Vestn. Kibernet., No. 4 (24), 50–57 (2016).
G. T. Bulgakova, L. A. Kalyakin, and M. M. Khasanov, Study of the stability of filtration of a gasified liquid, Prikl. Mekh. Tekh. Fiz., 41, No. 6, 78–85 (2000).
E. V. Berveno, A. A. Kalinkin, and Yu. M. Laevskii, Filtration of a two-phase liquid in an inhomogeneous medium on computers with distributed memory, Vestn. Tomsk. Gos. Univ., Mat. Mekh., No. 4 (30), 57–62 (2014).
A. I. Filippov and E. M. Devyatkin, Nonstationary temperature field during gas–liquid mixture filtration, Teplofiz. Vys. Temp., 39, No. 6, 962–969 (2001).
N. A. Zaitsev, B. V. Kritskii, and Yu. G. Rykov, On One Two-Dimensional Model for Calculating Two-Phase Flows, Preprint of the M. V. Keldysh Institute of Applied Mathematics, No. 86, Moscow (2014).
É. M. Abbasov and N. A. Agaeva, Modeling the process of liquid flow in the system "formation–pipeline," J. Eng. Phys. Thermophys., 94, No. 3, 559–570 (2021).
É. M. Abbasov and Kh. A. Feizullaev, Mathematical simulation of the processes of gas–liquid mixture flow in the bed and the pipe with allowance for the dynamic viscosity of the bed–well system, Zh. Vych. Mat. Mat. Fiz., 56, No. 1, 142–154 (2016).
I. A. Charnyi, Underground Hydrodynamics [in Russian], Gostoptekhizdat, Moscow (1963).
I. A. Charnyi, Unsteady Motion of Fluid in Pipes [in Russian], Nedra, Moscow (1975).
M. A. Guseinzade, L. I. Druchina, O. N. Petrova, and M. F. Stepanova, Hydrodynamic Processes in Complex Pipeline Systems [in Russian], Nedra, Moscow (1991).
I. G. Aramonovich, G. L. Lunts, and É. É. Él′sgol′ts, Functions of complex variable, in: Operational Calculus. Theory of Stability [in Russian], Nauka, Moscow (1968).
G. Doetsch, Guide to Applications of the Laplace Transforms [Russian translation], Nauka, Moscow (1965).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Inzhenerno-Fizicheskii Zhurnal, Vol. 96, No. 3, pp. 796–809, May–June, 2023.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Abbasov, É.M., Agaeva, N.A. Motion of a Gas–Liquid Mixture in the Bed–Pipeline System Subject to Heat Transfer. J Eng Phys Thermophy 96, 794–808 (2023). https://doi.org/10.1007/s10891-023-02741-w
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10891-023-02741-w