Skip to main content
SpringerLink
Log in

Generalized Model of Thermal Shock in Dynamic Thermoelasticity

  • HEAT CONDUCTION AND HEAT TRANSFER IN TECHNOLOGICAL PROCESSES
  • Published:
Journal of Engineering Physics and Thermophysics Aims and scope

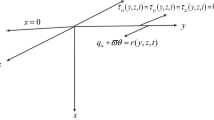
A generalized mathematical model of a thermal shock is developed in terms of dynamic thermoelasticity and its application to specific cases of intense heating of the solid body boundary, namely, of the temperature, thermal, heating by a medium. The model includes simultaneously three coordinate systems: Cartesian coordinates — a massive body bounded by a flat surface; spherical coordinates — a massive body with an internal spherical cavity; cylindrical coordinates — a massive body with an internal cylindrical cavity. The presence of curvature of the boundary surface dictates the initial formulation of the dynamic problem in displacements using the proposed "compatibility" equation in displacements for dynamic models. A numerical experiment was carried out and the wave nature of the propagation of a thermoelastic wave was described. Practically important engineering design relations are proposed for the upper estimate of thermal stresses through stress jumps at the front of a thermoelastic wave, obtained from operational solutions of dynamic problems. These relations allow one to quickly assess the degree of danger of short-term dynamic stresses.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. A. V. Luikov, Heat Conduction Theory [in Russian], Vysshaya Shkola, Moscow (1967).

    Google Scholar 

  2. É. M. Kartashov, Analytical Methods in the Theory of Thermal Conductivity of Solids [in Russian], Vysshaya Shkola, Moscow (2001).

    Google Scholar 

  3. V. S. Zarubin, Engineering Methods of Solving Heat Conduction Problems [in Russian], Énergoatomizdat, Moscow (1983).

    Google Scholar 

  4. V. F. Formalev, Equations of Mathematical Physics [in Russian], URSS, Moscow (2020).

    Google Scholar 

  5. A. V. Luikov, Application of the methods of thermodynamics of irreversible processes to the investigation of heat and mass transfer, J. Eng. Phys. Thermophys., 9, No. 3, 189–202 (1965).

    Article  Google Scholar 

  6. A. G. Shashkov, V. A. Bubnov, and S. Yu. Yanovskii, Wave Phenomena of Heat Conduction [in Russian], Nauka i Tekhnika, Minsk (1993).

  7. É. M. Kartashov, Model representations of thermal shock in dynamic thermoelasticity, Ross. Tekhnol. Zh., 8, No. 2, 85–108 (2020).

    Google Scholar 

  8. I. V. Kudinov and V. A. Kudinov, Mathematical simulation of the locally nonequilibrium heat transfer in a body with account for its nonlocality in space and time, J. Eng. Phys. Thermophys., 88, No. 2, 406–422 (2015).

    Article  Google Scholar 

  9. V. A. Kudinov, A. V. Eremin, and I. V. Kudinov, Development and study of a strongly nonequilibrium model of heat transfer in a liquid with space–time nonlocality, Teplofiz. Aéromekh., No. 6, 929–935 (2017).

  10. Yu. A. Kirsanov and A. Yu. Kirsanov, On measuring the time of thermal relaxation of solids, Izv. Ross. Akad. Nauk, Énergetika, No. 1, 113–122 (2015).

  11. Ya. S. Podstrigach, V. A. Lomakin, and Yu. M. Kolyano, Thermoelasticity of Bodies of Inhomogeneous Structure [in Russian], Nauka, Moscow (1984).

    MATH  Google Scholar 

  12. Yu. M. Kolyano, Methods of the Thermal Conductivity and Thermoelasticity of an Inhomogeneous Body [in Russian], Naukova Dumka, Kiev (1992).

    MATH  Google Scholar 

  13. V. L. Kolpashchikov and S. Yu. Yanovskii, Equation of dynamical thermoelasticity in a medium with thermal memory, J. Eng. Phys. Thermophys., 47, No. 4, 1241–1244 (1984).

    Article  Google Scholar 

  14. V. S. Zarubin and G. N. Kuvyrkin, Mathematical Models of Thermomechanics [in Russian], Fizmatgiz, Moscow (2002).

    Google Scholar 

  15. V. Novatskii, Review of works on dynamic problems of thermoelasticity. Mechanics, in: Collection of translations of foreign articles, Section 3: Mechanics of Deformable Solids, Vol. 6, 101–142 (1966).

  16. Yu. M. Kolyano, Generalized thermomechanics (Review), Mat. Metody Fiz.-Mekh. Polya, No. 2, 37–42 (1975).

  17. É. M. Kartashov and G. M. Bartenev, Dynamic effects in solids under conditions of intersection with intense energy flows, Itogi Nauki Tekh., Ser. Khim. Tekhnol. VMS, No. 25, 3–88 (1988).

  18. É. M. Kartashov and V. Z. Parton, Dynamic thermoelasticity and problems of thermal shock, Itogi Nauki Tekh., Ser. Mekh. Deformir. Tverd. Tela, No. 22, 55–127 (1991).

  19. É. M. Kartashov and V. A. Kudinov, Analytical Theory of Thermal Conductivity and Applied Thermoelasticity [in Russian], URSS, Moscow (2012).

    Google Scholar 

  20. É. M. Kartashov and E. V. Nenakhov, Model representations of the thermal shock in dynamic thermoelasticity, Izv. Ross. Akad. Nauk, Énergetika, No. 2, 1–22 (2019).

Download references

Author information

Authors and Affiliations

  1. Russian Technological University — MIRÉA (M. V. Lomonosov Institute of Fine Chemical Technologies), 78 Vernadskii Ave, Moscow, 119454, Russia

    É. M. Kartashov & S. S. Krylov

  2. Moscow Aviation Institute (National Research University), 4 Volokolamskoe Highway, Moscow, 125993, Russia

    É. M. Kartashov & S. S. Krylov

Authors
  1. É. M. Kartashov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. S. Krylov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to É. M. Kartashov.

Additional information

Translated from Inzhenerno-Fizicheskii Zhurnal, Vol. 96, No. 3, pp. 575–587, May–June, 2023

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kartashov, É.M., Krylov, S.S. Generalized Model of Thermal Shock in Dynamic Thermoelasticity. J Eng Phys Thermophy 96, 573–584 (2023). https://doi.org/10.1007/s10891-023-02719-8

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10891-023-02719-8

Keywords

Search

Navigation