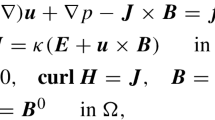Skip to main content
SpringerLink
Log in

Solution of the Stefan Two-Phase Problem with an Internal Source and of Heat Conduction Problems by the Method of Rapid Expansions

  • HEAT CONDUCTION AND HEAT TRANSFER IN TECHNOLOGICAL PROCESSES
  • Published:
Journal of Engineering Physics and Thermophysics Aims and scope

The Stefan two-phase problem with an internal source, as well as the heat conduction problem for rectangular and curvilinear regions, has been solved by the method of rapid sine-expansion, which involves the Fourier series. The problem of heat conduction in a body of rectangular form was solved in a general form with the Dirichlet conditions and an internal heat source by the method of rapid expansion, and thereafter the problem for a body of curvilinear shape. The solutions obtained were used in considering the Stefan problem with unknown curvilinear interface. Expressions are presented for matching the input data of the problem, on satisfaction of which the solution will be universally continuous everywhere in the region of the rectangle together with derivatives up to the sixth order inclusive. The nonfulfillment of these conditions leads to the discontinuity of the solution at the corner points. The algorithms of the solution of problems in rectangular and curvilinear regions, as well as of the Stefan twophase problem, are written. The solution for the rectangular region is represented in an explicit form, whereas the solution for the curvilinear region and the solution of the Stefan problem are reduced to a closed algebraic system of equations of small volume.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. É. M. Kartashov and G. S. Krotov, Analytical solution of the single-phase Stefan problem, in: Mathematical Modeling of Chemical-Technological Processes [in Russian], M. V. Lomonosov Moscow State Academy of Fine Chemical Technology, Moscow (2008), pp. 77–86.

  2. V. G. Melamed, Reduction of the Stefan problem to a system of ordinary differential equations, Izv. Akad. Nauk SSSR, Ser. Geofiz., No. 7, 848–869 (1958).

  3. A. D. Chernyshov, Concerning a certain Stefan problem, J. Eng. Phys. Thermophys., 7, No. 1, 77–79 (1964).

  4. É. M. Kartashov and V. A. Kudinov, Analytical Theory of Heat Conduction and of Applied Thermoelasticity [in Russian], URSS, Moscow (2018).

  5. N. A. Parfent’eva and I. G. Bobkova, On problems with phase transformations; www.vestnik/vgasu.ru.

  6. A. D. Chernyshov, Solution of a plane, axisymmetric and three-dimensional single-phase Stefan problem, J. Eng. Phys. Thermophys., 27, No. 2, 1022–1028 (1974).

    Article  MathSciNet  Google Scholar 

  7. V. B. Pen’kov and L. V. Satalkina, Method of Boundary States with Perturbations: Inhomogeneous and nonlinear problems of elasticity and thermoelasticity theory [in Russian], LAP Lambert Academic Publishing GmbH & Co., Saarbrucken (2012).

  8. N. A. Okulov, Concerning one method of solving one-dimensional Stefan problems, Vych. Metody Programmir., 12, Issue 2, 238–246 (2011).

    Google Scholar 

  9. D. A. Krylov, Approaches to solution of three-dimensional, heat conduction problems with account for phase transitions in dispersed media; http://sntbul.bmstu.ru/doc/562218.html.

  10. I. A. Ermolaev and A. I. Zhbanov, Mixed convection in a vertical channel with discrete heat sources on the wall, Izv. Ross. Akad. Nauk, Mekh. Zhidk. Gaza, No. 4, 40–46 (2009).

  11. L. A. Moiseeva and S. G. Cherkasov, Mathematical simulation of natural convection and heat transfer in a cryogenic fuel tank with a freezing heat exchanger, Izv. Ross. Akad. Nauk, Mekh. Zhidk. Gaza, No. 3, 39–46 (1997).

  12. A. M. Khludnev, The problem on the equilibrium thermoelastic plate with a crack, Sib. Mat. Zh., 37, No. 2, 452–463 (1996).

  13. A. A. Selyutin, The third boundary-value problem on the equilibrium of a thermoelastic plate with a crack, Sib. Zh. Ind. Matemat., 3, No. 2, 180–198 (2000).

    MathSciNet  MATH  Google Scholar 

  14. E. V. Stefanyuk, Analytical solutions of heat conduction problems at time-variable heat sources, Vestn. Samarsk. Gos. Tekhn. Univ., Ser. Tekhn. Nauki, No. 1(23), 204–213 (2009).

  15. V. S. Loginov, Heat transfer in a plate subjected to the action of internal heat sources at small Fourier numbers (Fo < 0.001), Izv. Tomsk. Politekh. Univ., 306, No. 2, 40–41 (2003).

  16. G. B. Shoev, E. A. Bodnar’, G. P. Oblapenko, and E. V. Kustova, Development and testing of the method of numerical modeling of thermally nonequilibrium dissociating flows in ANSYS Fluent, Teplofiz. Aéromekh., 23, No. 2(98), 159–172 (2016).

  17. V. I. Vasil’ev, M. V. Vasil’eva, Yu. M. Laevskii, and T. S. Timofeeva, Numerical simulation of two-phase liquid filtration in homogeneous media, Sib. Zh. Ind. Mat., 20, No. 2, 33–40 (2017).

  18. A. N. Konovalov and Yu. P. Popov, Optimal explicitly solvable discrete models with a controlled disbalance of full mechanical energy for dynamic problems of the linear elasticity theory, Sib. Mat. Zh., 56, No. 5, 1092–1099 (2015).

    Article  Google Scholar 

  19. M. V. Bondareva, E. N. Korzhov, and A. I. Shashkin, Models of turbulence for liquid flow in a circular gap, in: Collection of Papers Submitted to the Sci.-Techn. Conf. “Urgent Problems of Applied Mathematics, Information Science, and Mechanics,” 206–208 (2016).

  20. R. S. Volkov, G. V. Kuznetsov, and P. A. Strizhak, Analysis of the characteristics of the retardation and entrainment of droplets in a polydisperse water flow by high-temperature gases under conditions of intense phase transformations, J. Eng. Phys. Thermophys., 88, No. 4, 937–947 (2015).

    Article  Google Scholar 

  21. I. V. Derevich and A. A. Panova, Effects of random migration on the growth of the population of a biological system, J. Eng. Phys. Thermophys., 92, No. 6, 1375–1384 (2019).

    Article  Google Scholar 

  22. A. D. Chernyshov, Methods of rapid expansions for solving nonlinear differential equations, Zh. Vychisl. Mat. Mat. Fiz., 54, No. 1, 13–24 (2014).

    MATH  Google Scholar 

  23. N. S. Bakhvalov, N. P. Zhidkov, and G. M. Kobel’kov, Numerical Methods [in Russian], Nauka, Moscow (1987).

  24. N. S. Piskunov, Differential and Integral Calculus [in Russian], Izd. Fiz.-Mat. Lit., Moscow (1962), p. 856.

Download references

Author information

Authors and Affiliations

  1. Voronezh State University of Engineering Technologies, 19 Revolyutsiya Ave., Voronezh, 394000, Russia

    A. D. Chernyshov

Authors
  1. A. D. Chernyshov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. D. Chernyshov.

Additional information

Translated from Inzhenerno-Fizicheskii Zhurnal, Vol. 94, No. 1, pp. 101–120, January–February, 2021.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chernyshov, A.D. Solution of the Stefan Two-Phase Problem with an Internal Source and of Heat Conduction Problems by the Method of Rapid Expansions. J Eng Phys Thermophy 94, 95–112 (2021). https://doi.org/10.1007/s10891-021-02277-x

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10891-021-02277-x

Keywords

Search

Navigation