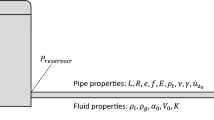
Nonstationary one-dimensional flow of a weakly-compressible fluid in a pipeline is considered. The flow is described by a nonlinear system of two partial differential equations for the fluid flow rate and pressure in the pipeline. An inverse problem on determination of the fluid pressure and flow rate at the beginning of the pipeline needed for the passage of the assigned quantity of fluid in the pipeline at a certain pressure at the pipeline end was posed and solved. To solve the above problem, a method of nonlocal perturbation of boundary conditions has been developed, according to which the initial problem is split at each discrete moment into two successively solvable problems: a boundary-value inverse problem for a differential-difference equation of second order for the fluid flow rate and a direct differential-difference problem for pressure. A computational algorithm was suggested for solving a system of difference equations, and a formula was obtained for approximate determination of the fluid flow rate at the beginning of the pipeline. Based on this algorithm, numerical experiments for model problems were carried out.
Similar content being viewed by others
References
I. A. Charnyi, Nonstationary Motion of Real Liquids in Tubes [in Russian], Nedra, Moscow (1975).
K. S. Basniev, N. M. Dmitriev, and G. D. Rozenberg, Oil–Gas Hydromechanics [in Russian], Inst. Komp. Issled., Moscow–Izhevsk (2005).
M. V. Lur’e, Mathematical Simulation of the Processes of Pipeline Transport of Oil, Oil Products, and Gas [in Russian], RGU Nefti i Gaza im. Gubkina, Moscow (2012).
O. M. Alifanov, E. A. Artyukhin, and S. V. Rumyantsev, Extreme Methods of Solving Ill-Posed Problems [in Russian], Nauka, Moscow (1988).
A. A. Samarskii and P. N. Vabishchevich, Numerical Methods of Solving Inverse Problems of Mathematical Physics [in Russian], Izd. LKI, Moscow (2009).
V. T. Borukhov and G. M. Zayats, Identification of a time-dependent source term in nonlinear hyperbolic or parabolic heat equation, Int. J. Heat Mass Transf., 91, 1106–1113 (2015).
P. N. Vabishchevich and V. I. Vasil’ev, Computational algorithms for solving the coefficient inverse problem for parabolic equations, Inverse Prob. Sci. Eng., 24, No. 1, 42–59 (2016).
Kh. M. Gamzaev, Numerical solution of combined inverse problem for generalized Burgers equation, J. Math. Sci., 221, No. 6, 833–839 (2017).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Inzhenerno-Fizicheskii Zhurnal, Vol. 93, No. 6, pp. 1622–1628, November–December, 2020.
Rights and permissions
About this article
Cite this article
Gamzaev, K.M. Inverse Problem of Pipeline Transport of Weakly-Compressible Fluids. J Eng Phys Thermophy 93, 1567–1573 (2020). https://doi.org/10.1007/s10891-020-02261-x
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10891-020-02261-x