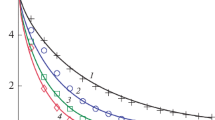
The authors have discussed the physical regularities of internal mass transfer in drying colloidal capillary-porous materials, which is characterized by the fact that in addition to the phenomenon of mass conductivity (diffusion of moisture) in a fixed coordinate system, the transfer of moisture by the matrix of the material due to its shrinkage is observed. As applied to this case, for a body in the shape of an unbounded plate dried symmetrically from both surfaces, a mathematical model has been written that describes mass conductivity and convective transfer of moisture in the body. The convective transfer of moisture depends on the normal coordinate to the plate’s surface: it is maximum at the surface of the plate and is equal to zero in its central plane. The authors have formulated the problem describing the process of symmetric drying of an unbounded plate on the basis of the convective-diffusion equation with a uniform initial distribution of the concentration and a boundary condition of mass transfer of the third kind. It has been noted that the formulated problem can be solved by numerical methods. For analysis of the degree of influence of the convective component on internal mass transfer, an analytical solution to the problem at constant parameters of the process has been obtained. According to the obtained solution, calculations of the change in the volume mean relative concentration as a function of the Fom number have been performed for the internal problem (Fom = 100) and the mixed diffusion problem (Fom = 10). It has been shown that the maximum effect of the influence of the convective component is observed for the intradiffusion problem.
Similar content being viewed by others
References
S. P. Rudobashta, Kinetic calculation of the process of convective drying of dispersed materials, Heat and Mass Transfer MMF–2000, IV Minsk Int. Forum, 22–26 May, 2000, Vol. 9, Heat and Mass Transfer in Drying Processes, Izd. Otd. Inst. Teplo- Massoobmena NAN Belarusi, Minsk (2000), pp. 41−48.
S. P. Rudobashta, Mathematical modeling of the process of convective drying of dispersed materials, Izv. Ross. Akad. Nauk, Énergetika, No. 4, 98−108 (2000).
S. P. Rudobashta, A. N. Planovskii, and É. N. Ochnev, Zonal method of calculation of continuous mass exchange apparatuses for systems with a solid phase, Teor. Osn. Khim. Tekhnol., VIII, No. 1, 22−29 (1974).
S. P. Rudobashta, Mass Transfer in Systems with a Solid Phase [in Russian], Khimiya, Moscow (1980).
A. V. Luikov, The Theory of Drying [in Russian], 2nd revised and enlarged edn., Énergiya, Moscow (1968).
B. Honarvar and D. Mowla, Theoretical and experimental drying of a cylindrical sample by applying hot air and infrared radiation in an inert medium fluidized bed, Brazilian J. Chem. Eng., 29, No. 2, 231−242 (2012).
C. Martínez-Vera and M. Vizcarra-Mendoza, Fluidized bed drying simulation considering solid Shrinkage, 6th Nordic Drying Conference, 5−7 June 2013, Copenhagen, Denmark (Electronic edition).
S. P. Rudobashta and É. M. Kartashov, Chemical Engineering. Diffusion Processes, Part 2 [in Russian], Yurait, Moscow (2018).
A. V. Luikov, Heat Conduction Theory [in Russian], Vysshaya Shkola, Moscow (1967).
F. Khanzadeh, H. Tavakolipour, and F. Rahmani, Convection drying kinetics of Asian white radish (Raphanus sativus L.) slices, 17th International Drying Symposium (IDS 2010), Magdeburg, Germany, 3−6 October 2010, Poster P 037, pp. 552−558 (Electronic edition).
J. Nastaj and T. Aleksandrzak, Modelowanie równowagi adsorpcji pary wodnej z fazy gazowej na zeolicie hisiv 3000, XIII Polish Drying Symposium, Szczecin, Kołobrzeg, 5–6 September 2013, No. 44 (Electronic edition).
H. Tavakoli-Pour, A. Kalbasi, and A. Basiri, Effect of drying parameters on quality index of Damghan pistachio and determination of effective diffusion indexes at modified conditions of this process, J. Food Sci. Technol., 5, No. 4, 47−56 (2008).
I. Doymaz, Drying kinetics of white mulberry, J. Food Eng., 61, 341−346 (2004).
J. M. F. Faustino, M. J. Barroca, and R. P. F. Guine, Study of the drying kinetics of green bell pepper and chemical characterization, Trans. Inst. Chem. Eng., 58, 163−170 (2007).
S. P. Rudobashta, G. Zueva, V. M. Dmitriev, and N. A. Zuev, Mass transfer in drying colloidal capillary-porous materials, Izv. Vyssh. Uchebn. Zaved., Khim. Khim. Tekhnol., 57, No. 1, 103–107 (2014).
S. P. Rudobashta and G. Zueva, Drying of seeds through oscillating infrared heating, Drying Technol., 34, No. 6, 505−515 (2016).
S. P. Rudobashta, G. A. Zueva, E. A. Muravleva, V. M. Dmitriev, Mass conductivity of capillary-porous colloidal materials subjected to convective drying, J. Eng. Phys. Thermophys., 91, No. 4, 845−853 (2018).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Inzhenerno-Fizicheskii Zhurnal, Vol. 93, No. 6, pp. 1446–1454, November–December, 2020.
Rights and permissions
About this article
Cite this article
Rudobashta, S.P., Kartashov, É.M. & Zueva, G.A. Mathematical Modeling of the Process of Convective Drying of Materials Taking into Account their Shrinkage. J Eng Phys Thermophy 93, 1394–1401 (2020). https://doi.org/10.1007/s10891-020-02244-y
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10891-020-02244-y