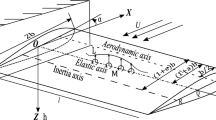
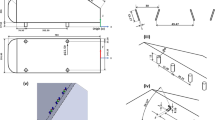
The method of solving the problem of external flow past a body for calculating the aerodynamic characteristics of projected bodies of complex geometrical shape is presented. Two approaches to the solution of the problem are considered: a numerical solution of the Favre-averaged Navier–Stokes equations with the use of the turbulence model and simulation of large vortices on the basis of the Navier–Stokes equations, in which numerical dissipation acts as a subgrid model of turbulence. Testing the results of calculations for the problem of flow past bodies by various methods showed their good correspondence to each other and with experimental data. For a projected body of a characteristic shape (missile) numerical simulation is made for a wide range of parameters: Mach numbers, angles of attack, and rotation speeds. Approximation dependences of the coefficients of aerodynamic forces and moments are constructed that can be used further for calculating the trajectories of projected bodies.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
A. A. Dmitrievskii and L. N. Lysenko, External Ballistics [in Russian], Mashinostroenie, Moscow (2005).
L. G. Loitsyanskii, Mechanics of Liquids and Gases [in Russian], Drofa, Moscow (2003).
A. M. Lipanov, Theoretical Hydrodynamics of Newtonian Media [in Russian], Nauka, Moscow (2011).
D. C. Wilcox, Turbulence Modeling for CFD, DCW Industries, California (1994).
B. E. Launder and D. B. Spalding, The numerical computation of turbulent flows, Comput. Methods Appl. Mech. Eng., 3, 269–289 (1974).
S. Sarkar and M. Y. Hussaini, Computation of the Sound Generated by Isotropic Turbulence, NASA Langley Research Center, Hampton (1993).
ANSYS 15.0, License No. 607281 from 30.09.2014, permanent.
A. M. Lipanov and S. A. Karskanov, Application of schemes of high order of approximation in modeling the processes of retardation of supersonic flows in rectangular channels, Vych. Mekh. Splosh. Sred, 6, No. 3, 292–299 (2013).
G.-S. Jiang and C.-W. Shu, Efficient implementation of weighted ENO schemes, J. Comput. Phys., 126, 202–228 (1996).
J. L. Steger and R. F. Warming, Flux vector splitting of the inviscid gas dynamic equations with application to finite-difference methods, J. Comput. Phys., 40, 263–293 (1981).
S. Gottlieb and C.-W. Shu, Total variation diminishing Runge–Kutta schemes, Math. Comput., 67, No. 221, 73–85 (1998).
G. G. Chernyi, Gas Flow with a High Supersonic Velocity [in Russian], Fizmatgiz, Moscow (1959).
I. G. Rusyak, A. I. Karpov, S. A. Korolev, and S. A. Karskanov, Calculation of the trajectory of motion of a missile in the atmosphere with account for the hydrodynamics of flow around it, Vopr. Oboron. Tekh., Ser. 14, Issue 2, 130–141 (2015).
Ivan Rusyak, Vadim Sufiyanov, Stanislav Korolev, and Mikhail Ermolaev, Software complex for simulation of internal and external ballistics of artillery shot, Int. Conf. on Military Technologies 2015 (ICMT 2015), Brno, May 19–21, 2015: University of Defence, Brno (2015), pp. 9–17; DOI: https://doi.org/10.1109/MILTECHS.2015.7153682.
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Inzhenerno-Fizicheskii Zhurnal, Vol. 92, No. 2, pp. 496–504, March–April, 2019.
Rights and permissions
About this article
Cite this article
Lipanov, A.M., Rusyak, I.G., Korolev, S.A. et al. Numerical Solution of the Problem of Flow Past Projected Bodies for Determining Their Aerodynamic Coefficients. J Eng Phys Thermophy 92, 477–485 (2019). https://doi.org/10.1007/s10891-019-01954-2
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10891-019-01954-2