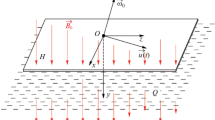
The motion of a viscous conducting medium caused by the rotation of an extended dielectric disk in an axial magnetic field in the presence of an axial temperature gradient is considered. For the case of a strong magnetic field, the values of the Nusselt number on the disk surface are estimated. A comparison of the obtained results with the well-known data of numerical calculation is made. Based on the calculated profile of the azimuthal velocity of the medium in the boundary layer on the disk, the motion of liquid is investigated in the space between two dielectric disks rotating in the same direction with different angular velocities in the presence of suction and blowing through their solid porous surfaces. The results of calculation of the angular rotational velocities of an inviscid core depending on the suction and magnetic field parameters are given.
Similar content being viewed by others
References
L. A. Dorfman, Hydrodynamic Resistance and Heat Transfer of Rotating Bodies [in Russian], Fizmatgiz, Moscow
V. D. Borisevich, V. D. Borman, G. A. Sulaberidze, A. V. Tikhomirov, and V. I. Tokmantsev, Physical Principles of Isotope Separation in a Gas Centrifuge [in Russian], Izd. Dom MÉI, Moscow (2011).
M. S. Kotel′nikova and B. A. Lugovtsov, On spontaneous swirling in axisymmetric MHD fl ows with closed streamlines of a perfectly conducting liquid, Prikl. Mekh. Tekh. Fiz., 48, 40–45 (2007).
E. G. Kaveeva and V. A. Rozhanskii, Poloidal and toroidal flows in the tokamak plasma near the magnetic island, Pis′ma Zh. Tekh. Fiz., 30, No. 13, 19–24 (2004).
D. Wang, Y. Wang, Z. Sun, et al., High-efficiency mixing process in secondary rotating stream, Chem. Eng. J., 313, 807–814 (2017).
V. D. Borisevich and E. P. Potanin, Laminar magnetohydrodynamic boundary layer on a disk in the presence of external rotating flow and suction, J. Eng. Phys. Thermophys., 89, No. 6, 1591–1597 (2016).
A. I. Karchevskii and E. P. Potanin, Plasma centrifuges, in: V. Yu. Baranov (Ed.), Isotopes: Properties, Obtaining, Application [in Russian], Fizmatlit, Moscow (2005), Vol. 1, pp. 326–338.
E. P. Potanin, A. I. Karchevskii, and A. L. Ustinov, On multiplication of the primary effect in a plasma centrifuge with crossed E × B fields, Zh. Tekh. Fiz., 48, No. 3, 472–478 (1978).
E. P. Velikhov, Stability of flow of a perfectly conducting liquid between rotating cylinders in a magnetic field, Zh. Éksp. Teor. Fiz., 36, 1398–1404 (1959).
S. Stemmley, E. Blackman, K. Caspary, E. Gilson, D. Hung, H. Ji, and P. Sloboda, Hydrodynamic magnetorotational instability analog experiment, Bull. Am. Phys. Soc., 61, No. 18, abstract id. JP10.059 (2016).
T. Nunez, E. Gilson, K. Caspary, F. Ebrahimi, J. Goodman, H. Ji, and X. Wei, Computer simulations of the magnetorotational instability (MRI) using the spectral finite-element Maxwell and Navier–Stokes (SFEMaNS) code, Bull. Am. Phys. Soc., 61, No. 18, abstract id. JP10.066 (2016).
I. V. Khalzov, A. I. Smolyakov, and V. I. Ilgisonis, Equilibrium magnetohydrodynamic flows of liquid metals in agnetorotational instability experiments, J. Fluid Mech., 644, 257−280 (2010).
N. M. Gorshunov and E. P. Potanin, Three-dimensional flows of a plasma rotating near solid surfaces in an axial magnetic field, Fiz. Plazmy, 42, No. 11, 1003–1012 (2016).
M. R. Malik, S. P. Wilkinson, and S. A. Orshag, Instability and transition of flow on a rotating disk, Robototekh. Tekh. Kibern., 19, No. 10, 34–44 (1981).
V. D. Borisevich and E. P. Potanin, Magnetohydrodynamic phenomena and heat transfer near a rotating disk, J. Eng. Phys. Thermophys., 88, No. 6, 1513–1521 (2015).
A. G. Kulikovskii and G. A. Lyubimov, Magnetohydrodynamics [in Russian], GIFML, Moscow (1962).
G. W. Sutton and A. Sherman, Engineering Magnetohydrodynamics [Russian translation], Mir, Moscow (1968).
W. S. King and W. S. Lewellen, Boundary layer similarity solutions for rotating flows with and without magnetic interaction, Phys. Fluids, 7, No. 10, 1674−1680 (1964).
E. P. Potanin, Three-dimensional motion of a gas in a rotating cylinder with a rotating cap, Mekh. Zhidk. Gaza, No. 1, 78–87 (2013).
L. P. Gorbachev and E. P. Potanin, On calculation of the MHD boundary layer on disks, Magn. Gidrodin., No. 2, 93–96 (1969).
E. M. Sparrow and R. D. Cess, Magnetohydrodynamic flow and heat transfer about a rotating disk, J. Appl. Mech., 29, 181−187 (1962).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Inzhenerno-Fizicheskii Zhurnal, Vol. 92, No. 1, pp. 174–180, January–February, 2019.
Rights and permissions
About this article
Cite this article
Borisevich, V.D., Potanin, E.P. Magnetohydrodynamics and Heat Transfer in Rotating Flows. J Eng Phys Thermophy 92, 169–175 (2019). https://doi.org/10.1007/s10891-019-01919-5
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10891-019-01919-5