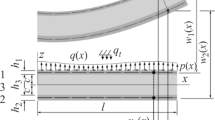
This paper considers the change in the stressed state of a three-layer elastoplastic rod with a compressible filler in a heat flow. The temperature change was calculated with the help of the formula obtained by averaging the thermal properties of the materials of the layers over the rod thickness. To describe kinematically the thickness asymmetric stack, broken line hypotheses were assumed: in thin bearing layers Bernoulli hypotheses hold; in the thin thickness-compressible filler the Timoshenko hypothesis with a linear approximation of displacements in the layer thickness holds. The work of the filler in the tangential direction is taken into account. The physical relations between stresses and deformations agree with the theory of small elastic deformations. The system of differential equilibrium equations was obtained by the variational method. At the boundary, kinetic conditions of rest of rod ends on rigid supports fixed in the space are assumed. The solution of the boundary-value problem was reduced to the obtaining of four sought functions — bendings and longitudinal displacements of median surfaces of the bearing layers. The analytical solution was obtained by the method of elastic solutions in the case of uniformly distributed continuous and local loadings. Its numerical analysis has been carried out. The change in stresses on the outer planes of the rod layers and in the cross section in the middle of the rod under the action of the heat flow has been investigated.
Similar content being viewed by others
Change history
30 April 2019
The second author's name should read <Emphasis Type="Bold">D. V. Leonenko</Emphasis>
References
V. V. Bolotin and Yu. N. Novichkov, Mechanics of Multilayer Structures [in Russian], Mashinostroenie, Moscow (1980).
Yu. M. Pleskachevskii, É. I. Starovoitov, and D. V. Leonenko, Mechanics of Three-Layer Rods and Plates Bound to an Elastic Base [in Russian], Fizmatlit, Moscow (2011).
I. Ivañez, M. M. Moure, S. K. Garcia-Castillo, and S. Sanchez-Saez, The oblique impact response of composite sandwich plates, Compos. Struct., No. 133, 1127–1136 (2015).
N. Grover, B. N. Singh, and D. K. Maiti, An inverse trigonometric shear deformation theory for supersonic flutter characteristics of multilayered composite plates, Aerospace Sci. Technol., No. 52, 41–51 (2016).
L. Škec and G. Jelenić, Analysis of a geometrically exact multi-layer beam with a rigid interlayer connection, Acta Mech., 225, No. 2, 523–541 (2014).
E. L. Kuznetsova, D. V. Leonenko, and E. I. Starovoitov, Natural vibrations of three-layer circular cylindrical shells in an elastic medium, Mech. Solids, 50, No. 3, 359–366 (2015).
A. G. Gorshkov, É. I. Starovoitov, and A. V. Yarovaya, Harmonic loading of sandwich viscoelastoplastic systems, Izv. Ross. Akad. Nauk, Mekh. Tverd. Tela, No. 6, 91–98 (2000).
E. I. Starovoitov, D. V. Leonenko, and A. V. Yarovaya, Circular sandwich plates under local impulsive loads, Int. Appl. Mech., 39, No. 8, 945–952 (2003).
É. I. Starovoitov and D. V. Leonenko, Dynamics of circular three-layer plates with elastic base under axisymmetric loading, Strength Mater., 42, No. 3, 322–330 (2010).
E. I. Starovoitov and D. V. Leonenko, Resonant effects of local on circular sandwich plates on en elastic foundation, Int. Appl. Mech., 46, No. 1, 86–93 (2010).
D. V. Leonenko and E. I. Starovoitov, Thermal impact on a circular sandwich plate on an elastic foundation, Mech. Solids, 47, No. 1, 111–118 (2012).
E. I. Starovoitov and D. V. Leonenko, Impact of thermal and ionizing radiation on a circular sandwich plate on an elastic foundation, Int. Appl. Mech., 47, No. 5, 580–589 (2011).
I. V. Kudinov and V. A. Kudinov, Determination of dynamic stresses in an infinite plate on the basis of an exact analytical solution of the hyperbolic heat-conduction equation for it, J. Eng. Phys. Thermophys., 88, No. 2, 388–405 (2015).
Yu. V. Nemirovskii and A. P. Yankovskii, Asymptotic analysis of the solution of the problem of nonstationary heat conduction of sandwich anisotropic inhomogeneous plates for small Biot numbers on faces, J. Eng. Phys. Thermophys., 81, No. 6, 1076-1087 (2008).
A. G. Gorshkov, E. I. Starovoitov, and A. V. Yarovaya, Cyclic loading of elastic-plastic bodies in neutron flux, Mech. Solids, 36, No. 1, 64–69 (2001).
E. I. Starovoitov and D. V. Leonenko, Thermoelastic bending of a sandwich ring plate on an elastic foundation, Int. Appl. Mech., 44, No. 9, 1032–1040 (2008).
D. V. Leonenko and E. I. Starovoitov, Thermoplastic strain of circular sandwich plates on an elastic base, Mech. Solids, 44, No. 5, 744–755 (2009).
E. I. Starovoitov, D. V. Leonenko, and A. V. Yarovaya, Elastoplastic bending of a sandwich bar on an elastic foundation, Int. Appl. Mech., 43, No. 4, 451–459 (2007).
D. V. Leonenko and E. I. Starovoitov, Deformation of a three-layer elastoplastic beam on an elastic foundation, Mech. Solids, 46, No. 2, 291–298 (2011).
E. I. Starovoitov, Yu. M. Pleskachevskii, D. V. Leonenko, and D. V. Tarlakovskii, Deformation of a step composite beam in a temperature field, J. Eng. Phys. Thermophys., 88, No. 4, 1023–1029 (2015).
É. I. Starovoitov, D. V. Leonenko, and D. V. Tarlakovskii, Thermal-force deformation of a physically nonlinear threelayer stepped rod, J. Eng. Phys. Thermophys., 89, No. 6, 1582–1590 (2016).
A. G. Gorshkov, É. I. Starovoitov, and D. V. Tarlakovskii, The Theory of Elasticity and Plasticity [in Russian], Fizmatlit, Moscow (2011).
A. A. Il’yushin, Plasticity, Pt. 1. Elastoplastic Deformations [in Russian], Gostekhizdat, Moscow (1948).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Inzhenerno-Fizicheskii Zhurnal, Vol. 92, No. 1, pp. 64–76, January–February, 2019.
Rights and permissions
About this article
Cite this article
Starovoitov, É.I., Leonenko, L.V. Effect of Heat Flow on the Stressed State of a Three-Layer Rod. J Eng Phys Thermophy 92, 60–72 (2019). https://doi.org/10.1007/s10891-019-01907-9
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10891-019-01907-9