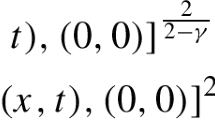Skip to main content
SpringerLink
Log in

Parabolic Profile in Heat-Conduction Problems. 1. Semi-Bounded Space with a Surface of Constant Temperature

  • Published:
Journal of Engineering Physics and Thermophysics Aims and scope

A new approach to the construction of constitutive integral relations, involving the introduction into consideration of local functions for a heat flow or a temperature determined directly from the differential heat-conduction equation, is proposed. With the use of this approach, new integral relations: the temperature-momentum integral of single modification, the temperature-momentum integral of double modification, the heat-flow integral, and the temperature-function integral, have been obtained. On the basis of these integrals as well as the integral method of heat balance and the refined integral method, different variants of the hybrid integral method realized with the use of manifold integral relations were investigated. In addition to the Langford norm, new error norms were introduced into consideration. The parabolic solutions obtained possess much better qualities compared to those of the analogous known solutions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. T. R. Goodman, Application of integral methods to transient nonlinear heat transfer, Adv. Heat Transf., Academic Press, New York (1964), Vol. 1, pp. 51–122.

  2. A. S. Wood, A new look at the heat balance integral method, Appl. Math. Model., 25, No. 10, 815–824 (2001).

    Article  Google Scholar 

  3. W. Braga and M. Mantelli, A new approach for the heat balance integral method applied to heat conduction problems, Proc. 38th AIAA Thermophys. Conf., Toronto, Ontario, Canada, Paper AIAA-2005-4686.

  4. D. Langford, The heat balance integral method, Int. J. Heat Mass Transf., 16, No. 12, 2424–2428 (1973).

    Article  Google Scholar 

  5. V. A. Kot, Method of boundary characteristics, J. Eng. Phys. Thermophys., 88, No. 6, 1390–1408 (2015).

    Article  Google Scholar 

  6. H. S. Carslow and J. C. Jaeger, Conduction of Heat in Solids, 2nd edn., Oxford University Press, Oxford, UK (1992).

  7. V. N. Volkov, A refinement of the Karman–Pohlhausen integral method in boundary layer theory, J. Eng. Phys. Thermophys., 9, No. 5, 371–374 (1965).

    Article  Google Scholar 

  8. V. N. Volkov and V. K. Li-Orlov, A refinement of the integral method in solving the heat conduction equation, Heat Transf. Sov. Res., 2, No. 2, 41–47 (1970).

    Google Scholar 

  9. N. Sadoun, E. K. Si-Ahmed, and P. Colinet, On the refined integral method for the one-phase Stefan problem with time-dependent boundary conditions, Appl. Math. Model., 30, No. 6, 531–544 (2006).

    Article  Google Scholar 

  10. N. Sadoun, E. K. Si-Ahmed, P. Colinet, and J. Legrand, On the Goodman heat-balance integral method for Stefan likeproblems: further considerations and refinements, Therm. Sci., 13, No. 2, 81–96 (2009).

    Article  Google Scholar 

  11. R. S. Gupta and N. C. Banik, Constrained integral method for solving moving boundary problems, Comput. Methods Appl. Mech. Eng., 67, No. 2, 211–221 (1988).

    Article  Google Scholar 

  12. R. S. Gupta and N. C. Banik, Diffusion of oxygen in a sphere with simultaneous absorption, Appl. Math. Model., 14, No. 3, 114–121 (1990).

    Article  Google Scholar 

  13. J. Hristov, The heat-balance integral method by a parabolic profile with unspecified exponent: Analysis and exercises, Therm. Sci., 13, No. 2, 27–48 (2009).

    Article  Google Scholar 

  14. A. Bejan, Second law analysis in heat transfer and thermal design, Advances in Heat Transfer, Academic Press, New York (1982), Vol. 1, pp. 1–58.

  15. Z. Kolenda, J. Donizak, and J. Hubert, On the minimum entropy production in steady-state heat conduction processes, Energy, 29, Nos. 12–13, 2441–2460 (2004).

  16. J. Hristov, Research note on a parabolic heat-balance integral method with unspecified exponent, Therm. Sci., 13, No. 2, 49–59 (2009).

    Article  Google Scholar 

  17. J. A. Esfahani and S. Koohi-Fayegh, Entropy generation analysis in error estimation an approximate solution a constant surface temperature semi-infinite conductive problem, Therm. Sci., 13, No. 2, 133–140 (2009).

    Article  Google Scholar 

  18. T. G. Myers, Optimizing the exponent in the heat balance and refined integral methods, Int. Commun. Heat Mass Transf., 36, No. 2, 143–147 (2009).

    Article  Google Scholar 

  19. J. Hristov, The heat-balance integral: 1. How to calibrate the parabolic profile? C. R. Acad. Sci. Mec., 340, No. 7, 485–492 (2012).

    MathSciNet  Google Scholar 

  20. J. Hristov, The heat-balance integral: 2. Parabolic profile with a variable exponent: The concept, analysis and numerical experiments, C. R. Acad. Sci. Mec., 340, No. 7, 493–500 (2012).

    MathSciNet  Google Scholar 

  21. S. L. Mitchell and T. G. Myers, Improving the accuracy of heat balance integral methods applied to thermal problems with time dependent boundary conditions, Int. J. Heat Mass Transf., 53, No. 17, 3540–3551 (2010).

    Article  Google Scholar 

  22. T. F. Zien, Approximate calculation of transient heat conduction, AIAA J., 14, No. 3, 401–406 (1976).

    Article  Google Scholar 

  23. T. F. Zien, Integral solution of ablation problems with time-dependent heat flux, AIAA J., 16, No. 12, 1287–1295 (1978).

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. A. V. Luikov Heat and Mass Transfer Institute, National Academy of Sciences of Belarus, 15 P. Brovka Str., 220072, Minsk, Belarus

    V. A. Kot

Authors
  1. V. A. Kot
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to V. A. Kot.

Additional information

Translated from Inzhenerno-Fizicheskii Zhurnal, Vol. 91, No. 6, pp. 1463–1484, November–December, 2018.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kot, V.A. Parabolic Profile in Heat-Conduction Problems. 1. Semi-Bounded Space with a Surface of Constant Temperature. J Eng Phys Thermophy 91, 1391–1412 (2018). https://doi.org/10.1007/s10891-018-1873-1

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10891-018-1873-1

Keywords

Search

Navigation