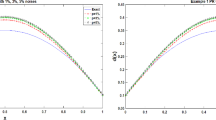
The problem on heat conduction of an infinite plate with a heat-transfer coefficient changing linearly with time for third-kind boundary conditions was solved analytically based on determination of the front of a temperature disturbance in this plate and introduction of additional boundary conditions. On the basis of the solution obtained, graphs of the distribution of isotherms in the indicated plate and the velocities of their movement along a spatial variable in it were constructed. As a result of the solution of the inverse problem on the heat conduction of the infinite plate with the use of the results of numerical calculation of the change in its temperature at any point on the indicated spatial coordinate, the Predvoditelev number was identified with an accuracy of 2%, which made it possible to determine the time dependence of the heat-transfer coefficient of the plate.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
V. L. Sergeev, A. G. Shashkov, and L. A. Sergeeva, Infl uence of the calorimetric-element characteristics on the results of heat-fl ux measurements, J. Eng. Phys. Thermophys., 15, No. 4, 967–971 (1968).
N. V. Shumakov, Method of Successive Intervals in the Heat Metering of Nonstationary Processes [in Russian], Atomizdat, Moscow (1979).
A. N. Tikhonov and V. Ya. Arsenin, Methods of Solving Ill-Posed Problems [in Russian], Nauka, Moscow (1974).
O. M. Alifanov, Inverse Problems of Heat Transfer [in Russian], Mashinostroenie, Moscow (1988).
O. M. Alifanov, Identifi cation of the Processes of Heat Transfer of Flying Vehicles [in Russian], Mashinostroenie, Moscow (1979).
É. M. Kartashov, Analytical Methods in the Heat Conduction Theory of Solid Bodies [in Russian], 3rd edn., Vysshaya Shkola, Moscow (2001).
V. A. Kudinov and I. V. Kudinov, Methods of Solving Parabolic and Hyperbolic Heat Conduction Equations [in Russian], Kn. Dom "Librokom," Moscow (2011).
V. A. Kudinov, É. M. Kartashov, and E. V. Stefanyuk, Technical Thermodynamics and Heat Transfer [in Russian], 2nd edn., Izd. "Yurait," Moscow (2012).
I. V. Kudinov and V. A. Kudinov, Analytical Solutions of Parabolic and Hyperbolic Heat and Mass Transfer Equations [in Russian], INFRA-M, Moscow (2013).
V. A. Kudinov and E. V. Stefanyuk, Heat conduction problems based on the determination of the temperature-disturbance front, Izv. Ross. Akad. Nauk, Énergetika, No. 5, 141–157 (2008).
A. V. Luikov, Heat Conduction Theory [in Russian], Vysshaya Shkola, Moscow (1967).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Inzhenerno-Fizicheskii Zhurnal, Vol. 88, No. 3, pp. 663–673, May–June, 2015.
Rights and permissions
About this article
Cite this article
Kudinov, V.A., Eremin, A.V. & Stefanyuk, E.V. Analytical Solutions of Heat-Conduction Problems with Time-Varying Heat-Transfer Coefficients. J Eng Phys Thermophy 88, 688–698 (2015). https://doi.org/10.1007/s10891-015-1238-y
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10891-015-1238-y