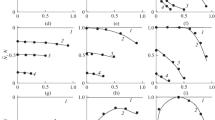
Based on diffusion concepts, the problem of deposition of monodisperse large Stokesian particles in a stirred plane layer with a vertically moving free boundary has been formulated and solved.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
J. Crank, Free and Moving Boundary Problems, Clarendon Press, Oxford (1984).
D. A. Tarzia, A bibliography on moving-free boundary problems for the heat-diffusion equation. The Stefan and related problems, MAT, Series A, No. 2, 297–301 (2000).
S. C. Gurta, The Classical Stefan Problem: Basic Concepts, Modeling and Analysis, Elsevier, London (2003).
V. V. Krasil’nikov, S. E. Savotchenko, and I. V. Udovenko, Diffusional models of growth of thin films and nanoclusters, Nauch. Vedom., No. 6 (26), Issue 12, 107–113 (2006).
V. A. Gorodtsov, Convective heat conduction and diffusion in the one-dimensional hydrodynamics, Zh. Éksp. Teor. Fiz., 116, Issue 5(11), 1616–1629 (1999).
M. K. Zhekamukhov and V. K. Kumykov, Modeling the process of ceramics metallization under vacuum, in: Phase Transitions, Ordered States, and New Materials, No. 2, 1–4 (2007).
R. N. Nigmatulin, Principles of the Mechanics of Heterogeneous Media [in Russian], Nauka, Moscow (1978).
I. A. Burovoi and A. Kh. Ibraev, A mathematical model of the process of mixing and separation of a polydisperse material in a bubbling bed, Izv. Vyssh. Uchebn. Zaved., Tsvetn. Metall., 14, No. 1, 136–139 (1971).
A. N. Verigin and S. V. Vasil’ev, Duffusion and sedimentation of a finely divided homogeneous suspension in settlers, Teor. Osn. Khim. Tekhnol., 16, No. 3, 374–380 (1982).
V. M. Kharin, V. I. Ryazhskikh, and R. M. Zavodskikh, Deposition of cryogenic suspensions in reservoirs, Teor. Osn. Khim. Tekhnol., 25, No. 5, 659–669 (1991).
É. M. Kartashov, Analytical methods of solution of boundary-value problems of nonstationary heat conduction in regions with moving boundaries, Inzh.-Fiz. Zh., 74, No. 2, 171–195 (2001).
V. M. Kharin and V. I. Ryazhskikh, Toward the theory of deposition, Teor. Osn. Khim. Tekhnol., 23, No. 5, 651–658 (1989).
G. Detch, Handbook on Applying the Laplace and Z Transformations [in Russian], Fizmatgiz, Moscow (1971).
N. M. Belyaev and A. A. Ryadno, Methods of the Theory of Heat Conduction [in Russian], Pt. 1, Nauka, Moscow (1982).
P. Joos, Dynamic Surface Phenomena, VSPBV, AH Zeist, The Netherlands (1999).
A. A. Samarskii and P. N. Vabishchevich, Computational Heat Transfer [in Russian], Editorial URSS, Moscow (2003).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Inzhenerno-Fizicheskii Zhurnal, Vol. 86, No. 6, pp. 1206–1211, November–December, 2013.
Rights and permissions
About this article
Cite this article
Ryazhskikh, A.V., Boger, A.A., Slyusarev, M.I. et al. Sedimentation of a Stokesian Monodisperse Large Particle Suspension in a Stirred Layer with a Moving Free Boundary. J Eng Phys Thermophy 86, 1280–1285 (2013). https://doi.org/10.1007/s10891-013-0951-7
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10891-013-0951-7