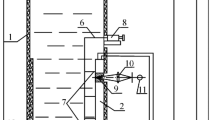
We have performed a numerical analysis of the nonstationary turbulent natural convection in a closed region with heat-conducting walls of finite thickness and a heat source located at the cavity base under the conditions of convective-radiative heat exchange with the environment. Typical distributions of the thermohydrodynamic parameters (streamlines, temperature field, field of the kinetic energy of turbulence, and dissipation field of the kinetic energy of turbulence) in a fairly wide range of Grashof numbers 107 ≤ Gr ≤ 109 have been obtained. Results characterizing the scales of influence of the nonstationarity factor and the relative heat conductivity coefficient of the material of the surrounding walls on the heat transfer intensity are presented. A correlation for determining the average Nusselt number on the heat source surface has been established.
Similar content being viewed by others

References
Y. Jaluria, Design and Optimization of Thermal Systems, McGraw-Hill, New York (1998).
S. Sathe and B. Sammakia, A review of recent developments in some practical aspects of air-cooled electronic packages, ASME J. Heat Transfer, 120, 830–839 (1998).
T. Icoz and Y. Jaluria, Design of cooling systems for electronic equipment using both experimental and numerical inputs, ASME J. Elec. Packag., 126, 465–471 (2005).
T. Icoz, N. Verma, and Y. Jaluria, Design of air and liquid cooling systems for electronic components using concurrent simulation and experiment, ASME J. Elec. Packag., 128, 466–478 (2006).
G. N. Dul’nev and N. N. Tarnovskii, Thermal Regimes of Electronic Equipment [in Russian], Énergiya, Leningrad (1971).
G. N. Dul’nev, Heat and Mass Transfer in Radioelectronic Equipment [in Russian], Vysshaya Shkola, Moscow (1984).
G. V. Biryulin, V. I. Egorov, Yu. Yu. Popov, and L. A. Savintseva, Thermal regime of microassemblies, in: Scientific-Technical Bulletin of St. Petersburg State University and Heat and Mass Transfer Institute "Investigations and Developments in the Field of Physics and Instrument Making," Issue 31, 115–117 (2006).
L. G. Loitsyanskii, Fluid Mechanics [in Russian], Drofa, Moscow (2003).
Yu. A. Sokovishin and O. G. Martynenko, Introduction to the Theory of Free-Convection Heat Transfer [in Russian], Izd. LGU, Moscow (1982).
B. E. Launder and D. B. Spalding, The numerical computation of turbulent flows, Comput. Meth. Appl. Mech. Eng., 3, 269–289 (1974).
R. A. W. M. Henkes, Van Der Vlugt, and C. J. Hoogendoorn, Natural-convection flow in a square cavity calculated with low-Reynolds-number turbulence models, Int. J. Heat Mass Transfer, 34, 377–388 (1991).
E. V. Bruyatskii, Turbulent Stratified Jet Flows [in Russian], Naukova Dumka, Kiev (1986).
A. L. Luikov, Theory of Heat Conduction [in Russian], Vysshaya Shkola, Moscow (1967).
N. Vardar, Numerical analysis of the transient turbulent flow in a fuel oil storage tank, Int. J. Heat Mass Transfer, 46, 3429–3440 (2003).
H. Ozoe, A. Mouri, M. Ohmuro, S. W. Churchill, and N. Lior, Numerical calculations of laminar and turbulent natural convection in water in rectangular channels heated and cooled isothermally on the opposing vertical walls, Int. J. Heat Mass Transfer, 28, 125–138 (1985).
K. J. Hsieh and F. S. Lien, Numerical modeling of buoyancy-driven turbulent flows in enclosures, Int. J. Heat Fluid Flow, 25, 659–670 (2004).
V. M. Paskonov, V. I. Polezhaev, and L. A. Chudov, Numerical Simulation of Heat and Mass Transfer Processes [in Russian], Nauka, Moscow (1984).
A. A. Samarskii, Theory of Difference Schemes [in Russian], Nauka, Moscow (1977).
H. N. Dixit and V. Babu, Simulation of high Rayleigh number natural convection in a square cavity using the lattice Boltzmann method, Int. J. Heat Mass Transfer, 49, 727–739 (2006).
P. Le Quere, Accurate solutions to the square thermally driven cavity at high Rayleigh number, Comput. Fluids, 20, 29–41 (1991).
S. M. Elsherbiny, G. D. Raithby, and K. G. T. Hollands, Heat transfer by natural convection across vertical and inclined layers, ASME J. Heat Transfer, 104, 96–102 (1982).
Y. Jaluria, Natural Convection: Heat and Mass Transfer [Russian translation], Mir, Moscow (1983).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Inzhenerno-Fizicheskii Zhurnal, Vol. 83, No. 2, pp. 326–337, March–April, 2010.
Rights and permissions
About this article
Cite this article
Kuznetsov, G.V., Sheremet, M.A. Turbulent regime of thermogravitational convection in a closed cavity. J Eng Phys Thermophy 83, 346–357 (2010). https://doi.org/10.1007/s10891-010-0351-1
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10891-010-0351-1