Skip to main content
SpringerLink
Log in

Pressure transient analysis of deformable reservoirs

  • Published:
Journal of Engineering Physics and Thermophysics Aims and scope

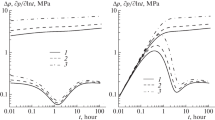
A new integrated methodology of evaluating the change in the permeability of a fractured or pressure-sensitive porous reservoir based on analytical or numerical simulation of a fluid inflow to a well has been proposed. The analysis draws on results of well tests. Analytical solutions of direct and inverse problems allow an evaluation of the permeability variation with decreasing pressure. Numerical simulation of an unsteadystate fluid inflow to a well (a direct problem) allows determining the diagnostic signs of variation in the reservoir permeability from the dynamics of the bottom hole pressure and an assessment of the evaluations obtained from solving an inverse problem. The methodology has been approved using results of some well tests.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. K. Aziz and A. Settari, Mathematical Simulation of Reservoir Systems [Russian translation], Nedra, Moscow (1982).

    Google Scholar 

  2. P. Quandalle and J. C. Sabathier, Typical features of a multipurpose reservoir simulator, SPE Reservoir Engineering, November, 1989, pp. 475–480.

  3. V. N. Shchelkachev, Principles and Applications of the Theory of Unsteady Filtration [in Russian], Pts. 1, 2, Neft’ i Gaz, Moscow (1995).

    Google Scholar 

  4. A. V. Raspopov and A. A. Shchipanov, Influence of dynamic deformation of a fractured-porous reservoir on oil production, Neft. Khoz., No. 6, 97–98 (2002).

    Google Scholar 

  5. A. A. Shchipanov, Influence of dynamic deformation of a fractured-porous reservoir on the effect produced by an increase in depression, Geol., Geofiz. Razrab. Neft. Gaz. Mestorozh., No. 2, 33–37 (2003).

  6. R. G. Shagiev, Well Tests Using Pressure Buildup Curves [in Russian], Nauka, Moscow (1998).

    Google Scholar 

  7. Yu. M. Molokovich, A. I. Markov, A. A. Davletshin, and G. G. Kushtanova, Piezometry of the Vicinity of Wells. Theoretical Principles [in Russian], Izd. “DAS,” Kazan’ (2000).

    Google Scholar 

  8. D. Bourdet, Well Test Analysis: the Use of Advanced Interpretation Models, Elsevier (2002).

  9. A. T. Gorbunov, Development of Anomalous Oil Fields [in Russian], Nedra, Moscow (1981).

    Google Scholar 

  10. V. D. Viktorin, A. F. Katoshin, and A. Yu. Nazarov, A geological field model of a bulk network of cracks (MBNC) of carbonate and sandstone collectors of fractured-porous type, in: Problems of Geology and Development of Intricately Built Reservoirs of Fractured-Porous Type, PermNIPIneft’, Perm’ (2003), pp. 60–117.

    Google Scholar 

  11. A. A. Shchipanov and A. Iu. Nazarov, Simulation of fluid flow in fractured reservoirs subject to deformation, AAPG International Conference & Exhibition. Proceedings, Paris, France (2005), pp. 1–6.

  12. R. N. Diyashev, A. V. Kosterin, and É. V. Skvortsov, Fluid Flow in Deformable Oil Reservoirs [in Russian], Izd. Kazansk. Mat. Ob., Kazan’ (1999).

    Google Scholar 

  13. K. S. Basniev, N. M. Dmitriev, and G. D. Rozenberg, Oil-Gas Hydromechanics [in Russian], Inst. of Computer Studies, Moscow–Izhevsk (2005).

    Google Scholar 

  14. D. K. Ponting, Corner point geometry in reservoir simulation, in: Proc. Joint IMA/SPE European Conf. on the Mathematics of Oil Recovery, July 1989, Cambridge (1989), pp. 1–8.

  15. A. A. Shchipanov, Program package of modeling multiphase fluid filtration and the possibilities of its application, Bulletin of Perm University. Information Systems and Technologies, Issue 5, 108–114 (2001).

  16. A. N. Tikhonov and V. Ya. Arsenin, Methods of Solving Ill-Posed Problems [in Russian], Nauka, Moscow (1979).

    Google Scholar 

  17. K. S. Basniev, I. N. Kochina, and V. M. Maksimov, Underground Hydromechanics [in Russian], Nedra, Moscow (1993).

    Google Scholar 

  18. N. P. Lebedinets, Study and Development of Oil Fields with Fractured Reservoir [in Russian], Nauka, Moscow (1997).

    Google Scholar 

  19. G. I. Marchuk, Methods of Computational Mathematics [in Russian], Nauka, Moscow (1980).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Perm State University, 15 Bukirev Str., Perm, 614990, Russia

    A. A. Shchipanov

Authors
  1. A. A. Shchipanov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. A. Shchipanov.

Additional information

Translated from Inzhenerno-Fizicheskii Zhurnal, Vol. 83, No. 2, pp. 235–247, March–April, 2010.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Shchipanov, A.A. Pressure transient analysis of deformable reservoirs. J Eng Phys Thermophy 83, 250–262 (2010). https://doi.org/10.1007/s10891-010-0340-4

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10891-010-0340-4

Keywords

Search

Navigation