Abstract
A new type of decomposition by population subgroup is proposed for the Gini inequality index. The decomposition satisfies the completely identical distribution (CID) condition, whereby the between-group inequality is null if and only if the distribution within each subgroup is identical to all the others. Thus, this decomposition contrasts strikingly with the subgroup decomposition of the generalized entropy measures, which satisfy the condition that the between-group inequality is null if the mean within each subgroup equals those of all the others. The new decomposition can be generalized to the distance-Gini index and the volume-Gini index, two multivariate Gini indices introduced by Koshevoy and Mosler, with some modification of the index definition and a somewhat loosened CID condition in the latter case. The source decomposition is also generalized to these multi-dimensional indices. Interaction terms appear among sources of different attributes in the decomposition for the modified volume–Gini index.


Similar content being viewed by others
Notes
The definition of “consistency with hierarchical grouping systems” in this paper is entirely different from that of “subgroup consistency” defined by Shorrocks [18].
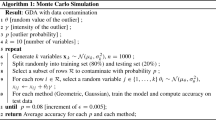
As noted above, estimates for the new decomposition are made from aggregates using the composite Simpson’s rule (with Eq. 9 for calculations of the between-group inequalities).
See footnote 1.
References
Anderson, G.: Indices and tests for multidimensional inequality: multivariate generalizations of the Gini coefficient and Kolmogorov–Smirnov two sample test. Paper prepare for the 28th general conference of the IARIW, Cork, Ireland, 22–28 Aug. 2004
Baringhaus, L., Franz, C.: On a new multivariate two-sample test. J. Multivar. Anal. 88, 190–206 (2004)
Bhattacharya, N., Mahalanobis, B.: Regional disparities in household consumption in India. J. Am. Stat. Assoc. 62, 143–161 (1967)
Dagum, C.: A new approach to the decomposition of the Gini income inequality ratio. Emp. Econ. 22, 515–531 (1997)
Easterlin, R.: Does economic growth improve the human lot? Some empirical evidence. In: David P., Reder M. (eds.) Nations and households in economic growth: essays in honour of Moses Abramobitz, pp. 89–125. Academic, New York (1974)
Easterlin, R.: Building a better theory of well-being. In: Bruni, L., Porta, P.L. (eds.) Economics and happiness: framing the analysis, pp. 29–64. Oxford University Press, New York (2006)
Gajdos, T., Weymark, J.A.: Multidimensional generalized Gini indices. Varnderbilt University Working Paper 3-W11R, Department of Economics, Varnderbilt University, Nashville, Tennessee (2003)
Gardner, R.J.: The Brunn–Minkowski inequality. Bull. Am. Math. Soc. 39, 355–405 (2002)
Helgason, S.: The Radon Transform. Birkhauser, Boston (1980)
Koshevoy, G.. A., Mosler, K.: The Lorenz zonoid of a multivariate distribution. J. Am. Stat. Assoc. 91, 873–882 (1996)
Koshevoy, G.A., Mosler, K.: Multivariate Gini indices. J. Multivar. Anal. 60, 252–276 (1997)
Koshevoy, G.A., Mosler, K.: Multivariate Lorenz dominace based on zonoids. Advance in Statistical Analysis 91, 57–76 (2007)
Lerman, R.I., Yitzhaki, S.: A note on the calculation and interpretation of the Gini index. Econ. Lett. 15, 363–368 (1984)
Oja, H.: Descriptive statistics for multivariate distributions. Stat. Probab. Lett. 1, 327–332 (1983)
Pyatt, G.: On the interpretation and disaggregation of Gini coefficients. Econ. J. 86, 243–255 (1976)
Rao, V.M.: Two decompositions of concentration ratio. J. R. Stat. Soc. A 132, 418–425 (1969)
Schneider, R.: Convex Bodies: The Brunn-Minkowski Theory. Cambridge University Press, New York (1993)
Shorrocks, A.: Aggregation issues in inequality measurement. In: W. Eichhorn (ed.) Measurement in Economics, pp. 429–451. Physica-Verlag, Heidelberg (1988)
Shorrocks, A., Wan, G.: Spatial decomposition of inequality. J. Economic Geography 5, 59–81 (2005)
Shephard, G.C.: Combinatorial properties of associated zonotopes. Can. J. Math. 26, 302–321 (1974)
Torgersen, E.: Comparison of Statistical Experiments. Cambridge University Press, Cambridge (1991)
Tsui, K.-Y.: Multidimensional inequality and multidimensional generalized entropy measures: an axiomatic derivation. Soc Choice Welf 16, 145–157 (1999)
Wilks, S.S.: Multidimensional statistical scatter. In: Olkin, et. al. (eds.) Contributions to Probability and Statistics, pp. 486–503. Stanford University Press, Stanford, (1960)
Yitzhaki, S., Lerman, R.I.: Income stratification and income inequality. Rev. Income Wealth 37, 313–329 (1991)
Acknowledgement
I wish to thank the editors and anonymous reviewers at this journal whose comments and suggestions have been very helpful to improve the paper.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Proofs
1.1.1 Proof of Eq. 16
On the assumption that F i is continuous, by applying integration by parts, cv(F i ,F) can be expanded as follows:
Note that ∫F i dF i =∫FdF=1/2. Then, using the equality \( {\int {F{\text{d}}F_{i} - 1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2 = - {\int {F_{i} {\text{d}}F + 1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2} }} }\) and the notation in section 2.3, Eq. 16 is obtained.
1.1.2 Proof of Eqs. 24 and 25
By applying the definition of cvD(F i ,F) in Eq. 22, the distance-Gini mean difference M D(F) can be expanded as follows:
Note that F = Σp i F i . Subtracting M D(F) from both sides after doubling, decomposition 24 is obtained. Equation 25 is easily derived by replacing F with \( \widetilde{F} \).
1.1.3 Range of the modified Torgersen index
Since
where \( {\sum\limits_i {{\left[ {0,e_{i} } \right]}} } + {\left[ {0, - \gamma } \right]} \) is the Minkowski sum of the line segments [0,e i ] (i = 1,...,d) and [0,−γ], and e i = {e ij } is a unit vector consisting of elements e ij = 0 if j ≠ i, or =1 if j = i, then, the volume of \( Z_{{\text{T}}} {\left( {\widetilde{F}\left| \gamma \right.} \right)}\) is less than or equal to the volume of \( {\sum\limits_i {{\left[ {0,e_{i} } \right]}} } + {\left[ {0, - \gamma } \right]} \), which is calculated at 1 + Σγ i by using the following formula \( {\text{vol}}{\left( {{\sum\limits_{i = 1}^n {{\left[ {0,a_{i} } \right]}} }} \right)} = {\sum\limits_{1 \leqslant i_{1} < \cdots < i_{d} < n} {{\left| {\det {\left( {a_{{i_{1} }} , \cdots ,a_{{i_{d} }} } \right)}} \right|}} }\) (e.g. [20]). Thus, the modified Torgersen index R T(F|γ) is less than or equal to unity.
Assume that F is an n-point d-variate distribution in which there is a different monopolist for each variable (attribute). Then, R T(F|γ) → 1 if n → ∞.
1.1.4 Proof of Eq. 41
By applying Eq. 38, Eq. 58 is derived.
where \( G{\left( \varepsilon \right)} = \varepsilon F_{i} + {\left( {1 - \varepsilon } \right)}F \). The modified Torgersen mean difference M T(G(ε)|γ) and the mixed volume MV d−1(F,G(ε)|γ) have the following derivatives at ε = 0:
The derivative of \({\text{cv}}_{{\text{T}}} {\left( {F,G{\left( \varepsilon \right)}\left| \gamma \right.} \right)} \) at ε = 0 equals zero from its definition and Eq. 59. Thus, the second term on the right-hand side of Eq. 58 → 0 if ε → 0. Since the left-hand side → \( {\text{cv}}_{{\text{T}}} {\left( {F_{i} ,F\left| \gamma \right.} \right)} \) if ε→0, Eq. 41 is derived.
1.1.5 Proof of the equality condition in Eq. 45 and the condition for null between-inequality in Eq. 47
It is trivial that \( {\text{cv}}_{{\text{V}}} {\left( {G,F\left| \gamma \right.} \right)} = 0{\text{ }}if{\text{ }}G^{s} = F^{s} \) for any coordinate axis, and \( Z_{{\text{T}}} {\left( {G\left| \gamma \right.} \right)} = Z_{{\text{T}}} {\left( {F\left| \gamma \right.} \right)} \)If \( {\text{cv}}_{{\text{V}}} {\left( {G,F\left| \gamma \right.} \right)} = 0 \), all terms constituting cvV(G,F|γ) in Eq. 45 should be zero, including cvT(G,F|γ). On the assumption that MT(F|γ)>0, this means that \( Z_{{\text{T}}} {\left( {G\left| \gamma \right.} \right)} = \alpha Z_{{\text{T}}} {\left( {F\left| \gamma \right.} \right)}\), where α is a positive constant, according to Minkowski’s first inequality concerning the mixed volume. Since cv(G s, F s) should also be zero at the same time, G s=F s for any coordinate axis. This forces α to be unity. Thus, the equality condition in Eq. 45 is proved.
If M T(F|γ)>0, the equality condition in Eq. 45 can be applied to the proof of the condition for the null between-inequality in Eq. 47. If M T(F|γ)=0, the Brunn-Minkowski inequality (e.g. [17]) asserts that Z T(F i |γ) is on the same hyperplane as Z T(F|γ). Let k 1,...,k t be the highest-dimensional sub-coordinate axes under the condition that \( M_{{\text{T}}} {\left( {F^{{j_{1} \cdots j_{s} }} \left| \gamma \right.} \right)} > 0 \). The equality condition in Eq. 45 asserts that \( Z_{{\text{T}}} {\left( {F^{{k_{1} \cdots k_{t} }}_{i} \left| \gamma \right.} \right)} = Z_{{\text{T}}} {\left( {F^{{k_{1} \cdots k_{t} }} \left| \gamma \right.} \right)} \) (Note that \( {\text{cv}}_{{\text{V}}} {\left( {F^{{k_{1} \cdots k_{t} }}_{i} ,F^{{k_{1} \cdots k_{t} }} \left| \gamma \right.} \right)} = 0 \) if \( {\text{cv}}_{{\text{V}}} {\left( {F_{i} ,F\left| \gamma \right.} \right)} = 0 \)). From this, ZT(F i |γ) should be identical to Z T(F|γ). G s = F s is true for any coordinate axis, irrespective of the value of M T(F|γ). Thus, the condition for null between-inequality in Eq. 47 is proved.
1.1.6 Proof of Eqs. 20 and 50
First, the proof of Eq. 50 is given inductively. Without loss of generality, we can assume that i = 1 and x={x 1,x 2,0,...,0} because of invariance for rotation on axis i and axis permutation. If d = 2, Eq. 50 can be proved as follows:
where a={cosθ,sinθ}, and \( {\bf x} = {\left\{ {x_{1} ,x_{2} } \right\}} = {\left\{ {{\left\| \bf x \right\|}\cos \varphi ,{\text{ }}{\left\| \bf x \right\|}\sin \varphi } \right\}} \). Assume that Eq. 50 is proved if the dimension is d−1. Then,
Equation 50 is derived by summing Eq. 50 over i after multiplying by x i .
Rights and permissions
About this article
Cite this article
Okamoto, M. Decomposition of gini and multivariate gini indices. J Econ Inequal 7, 153–177 (2009). https://doi.org/10.1007/s10888-007-9069-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10888-007-9069-5