Skip to main content
SpringerLink
Log in

Orbifold Hamiltonian Structures of Certain Quasi-Painlevé Equations

  • Published:
Journal of Dynamics and Differential Equations Aims and scope Submit manuscript

Abstract

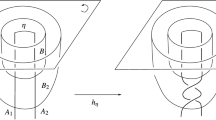
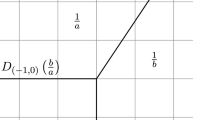
For each of two Hamiltonian systems with the quasi-Painlevé property, we establish a holomorphic orbifold Hamiltonian structure for the system on an augmented phase space obtained through blowups. This generalises the orbifold Hamiltonian structure of the first Painlevé equation on its Okamoto space of initial conditions constructed by Iwasaki and Okada. The Hamiltonian structure is provided by an appropriate orbifold atlas for the space and a collection of Hamiltonian functions which are polynomial in coordinates. In the quasi-Painlevé cases we consider, the Hamiltonian structure is with respect to a rational 2-form which is allowed to have certain zeroes, as opposed to holomorphic symplectic forms in the case of the Painlevé equations, which ensures the system is regularisable everywhere on the augmented phase space in a way that corresponds to the quasi-Painlevé property of the equation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Data Availibility Statement

Not applicable as no datasets were generated or analysed during the current study.

References

  1. Chiba, H.: The first, second and fourth Painlevé equations on weighted projective spaces. J. Differ. Equ. 260(2), 1263–1313 (2016)

    Article  Google Scholar 

  2. Filipuk, G., Halburd, R.G.: Movable algebraic singularities of second-order ordinary differential equations. J. Math. Phys. 50(2), 023509, 18 pp (2009)

  3. Filipuk, G., Stokes, A.: Takasaki’s rational fourth Painlevé-Calogero system and geometric regularisability of algebro-Painlevé equations. Nonlinearity 36(10), 5661–5697 (2023)

    Article  MathSciNet  Google Scholar 

  4. Filipuk, G., Stokes, A.: On Hamiltonian structures of quasi-Painlevé equations. J. Phys. A 56(49), 495205 (2023)

    Article  Google Scholar 

  5. Iwasaki, K., Okada, S.: On an orbifold Hamiltonian structure for the first Painlevé equation. J. Math. Soc. Jpn. 68(3), 961–974 (2016)

    Article  Google Scholar 

  6. Kecker, T.: Polynomial Hamiltonian systems with movable algebraic singularities. J. Anal. Math 129, 197–218 (2016)

    Article  MathSciNet  Google Scholar 

  7. Kecker, T., Filipuk, G.: Regularising transformations for complex differential equations with movable algebraic singularities. Math. Phys. Anal. Geom. 25, article number 9, 43 pp (2022)

  8. Matano, T., Matumiya, A., Takano, K.: On some Hamiltonian structures of Painlevé systems. II. J. Math. Soc. Jpn. 51(4), 843–866 (1999)

  9. Matumiya, A.: On some Hamiltonian structures of Painlevé systems. III. Kumamoto J. Math. 10, 45–73 (1997)

  10. Okamoto, K.: Sur les feuilletages associés aux équations du second ordre à points critiques fixes de P. Painlevé, (French) [On foliations associated with second-order Painlevé equations with fixed critical points], Japan. J. Math. (N.S.) 5(1), 1–79 (1979)

  11. Shimomura, S.: A class of differential equations of PI-type with the quasi-Painlevé property. Ann. Mat. Pura Appl. 186, 267–280 (2007)

    Article  MathSciNet  Google Scholar 

  12. Shimomura, S.: On second order nonlinear differential equations with the quasi-Painlevé property II, RIMS Kōkyūroku 1424, 177–183 (2005)

  13. Shimomura, S.: Nonlinear differential equations of second Painlevé type with the quasi-Painlevé property. Tohoku Math. J. (2) 60(4), 581–595 (2008)

  14. Shioda, T., Takano, K.: On some Hamiltonian structures of Painlevé systems. I. Funkcial. Ekvac. 40(2), 271–291 (1997)

  15. Takano, K.: Defining Manifolds for Painlevé Equations, Toward the Exact WKB Analysis of Differential Equations, Linear or Non-linear (Kyoto, 1998), 204, 261–269. Kyoto Univ. Press, Kyoto (2000)

Download references

Funding

GF acknowledges the support of the grant entitled “Geometric approach to ordinary differential equations" (01.03.2023–29.02.2024) funded under New Ideas 3B competition within Priority Research Area III implemented under the “Excellence Initiative - Research University” (IDUB) Programme (University of Warsaw) (nr 01/IDUB/2019/94). The work of GF is also partially supported by the project PID2021-124472NB-I00 funded by MCIN/AEI/10.13039/501100011033 and by “ERDF A way of making Europe". AS is supported by a Japan Society for the Promotion of Science (JSPS) Postdoctoral Fellowship for Research in Japan and also acknowledges the support of JSPS KAKENHI Grant Numbers 21F21775 and 22KF0073.

Author information

Authors and Affiliations

  1. Institute of Mathematics, University of Warsaw, ul. Banacha 2, 02-097, Warsaw, Poland

    Galina Filipuk

  2. Graduate School of Mathematical Sciences, The University of Tokyo, 3-8-1 Komaba, Tokyo, Meguro-ku, 153–8914, Japan

    Alexander Stokes

  3. Waseda Institute for Advanced Study, Waseda University, 1-21-1 Nishiwaseda, Tokyo, Shinjuku-ku, 169–0051, Japan

    Alexander Stokes

Authors
  1. Galina Filipuk
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Alexander Stokes
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

GF and AS jointly conceived and carried out the research reported in this manuscript and wrote the text jointly.

Corresponding author

Correspondence to Galina Filipuk.

Ethics declarations

Conflicts of interest

The authors have no competing interests to declare.

Ethical Approval

Not applicable.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Filipuk, G., Stokes, A. Orbifold Hamiltonian Structures of Certain Quasi-Painlevé Equations. J Dyn Diff Equat (2024). https://doi.org/10.1007/s10884-024-10352-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10884-024-10352-z

Keywords

Mathematics Subject Classification

Search

Navigation