Abstract
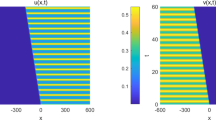
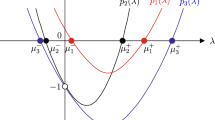
This paper concerns the propagation direction of the bistable traveling wave for a time-periodic Lotka–Volterra reaction–diffusion competition system. The speed is first shown to be bounded by the asymptotic spreading speeds of the monostable subsystems. General results toward the propagation direction are obtained by establishing two comparison principles on wave speed. These results rely on the establishment of the speed sign of an upper (or lower) solution to the system of wave profile equations. In particular, by subtly constructing upper or lower solutions, we derive a set of explicit formulas that determine whether the speed sign is positive or negative, which indicates whether the bistable traveling wave spatially propagates to the left or to the right. Finally, numerical simulations are given to demonstrate the effects of system parameters to the propagation direction of the bistable traveling wave.


Similar content being viewed by others
References
Alhasanat, A., Ou, C.: Minimal-speed selection of traveling waves to the Lotka–Volterra competition model. J. Differ. Equ. 266, 7357–7378 (2019)
Alhasanat, A., Ou, C.: On a conjecture raised by Yuzo–Hosono. J. Dyn. Diff. Equat. 31, 287–304 (2019)
Bao, X., Wang, Z.: Existence and stability of time periodic traveling waves for a periodic bistable Lotka–Volterra competition system. J. Differ. Equ. 255, 2402–2435 (2013)
Conley, C., Gardner, R.: An application of the generalized morse index to travelling wave solutions of a competitive reaction–diffusion model. Indiana Univ. Math. J. 33, 319–343 (1984)
Fang, J., Zhao, X.-Q.: Bistable traveling waves for monotone semiflows with applications. J. Eur. Math. Soc. 17, 2243–2288 (2015)
Gardner, R.: Existence and stability of traveling wave solutions of competition models: a degree theoretic approach. J. Differ. Equ. 44, 343–364 (1982)
Girardin, L., Nadin, G.: Travelling waves for diffusive and strongly competitive systems: Relative motility and invasion speed. Eur. J. Appl. Math. 26, 521–534 (2015)
Gourley, S., Ruan, S.: Convergence and travelling fronts in functional differential equations with nonlocal terms: a competition model. SIAM J. Math. Anal. 35, 806–822 (2003)
Guo, J.-S. Lin, Y.-C.: The sign of the wave speed for the Lotka–Volterra competition–diffusion system. Commun. Pure Appl. Anal. 12(5), 2083–2090 (2013)
Hosono, Y.: Singular perturbation analysis of traveling fronts for the Lotka–Volterra competing models. Numer. Appl. Math. 2, 687–692 (1989)
Hosono, Y.: The minimal speed of traveling fronts for diffusive Lotka–Volterra competition model. Bull. Math. Biol. 60, 435–448 (1998)
Huang, W.: Uniqueness of the bistable traveling wave for mutualist species. J. Dyn. Differ. Equ. 13, 147–183 (2001)
Huang, W.: Problem on minimum wave speed for a Lotka–Volterra reaction diffusion competition model. J. Dyn. Differ. Equ. 22, 285–297 (2010)
Huang, W., Han, M.: Nonlinear determinacy of minimum wave speed for Lotka–Volterra competition model. J. Differ. Equ. 251, 1549–1561 (2011)
Kan-on, Y.: Parameter dependence of propagation speed of traveling waves for competition diffusion equation. SIAM J. Math. Anal. 26, 340–363 (1995)
Kan-on, Y.: Fisher wave fronts for the Lotka–Volterra competition model with diffusion. Nonlinear Anal. 26, 145–164 (1997)
Li, W.-T., Lin, G., Ruan, S.: Existence of travelling wave solutions in delayed reaction–diffusion systems with applications to diffusion–competition systems. Nonlinearity 19, 1253–1273 (2006)
Liang, X., Yi, Y., Zhao, X.Q.: Spreading speeds and traveling waves for periodic evolution systems. J. Differ. Equ. 231(6), 57–77 (2006)
Liang, X., Zhao, X.-Q.: Asymptotic speeds of spread and traveling waves for monotone semiflows with applications. Commun. Pure Appl. Math. 60, 1–40 (2007)
Lin, G., Li, W.-T.: Bistable wavefronts in a diffusive and competitive Lotka–Volterra type system with nonlocal delays. J. Differ. Equ. 244, 487–513 (2008)
Ma, M., Huang, Z., Ou, C.: Speed of the traveling wave for the bistable Lotka–Volterra competition model. Nonlinearity 32, 3143–3162 (2019)
Tsai, J.-C., Weng, Y.-Y.: Propagation direction of traveling waves for a class of bistable epidemic models. J. Math. Biol. 81(6–7), 1465–1493 (2020)
Zhao, G., Ruan, S.: Existence, uniqueness and asymptotic stability of time periodic traveling waves for a periodic Lotka–Volerra competition system with diffusion. J. Math. Pures Appl. 95, 627–671 (2011)
Zhao, X.-Q.: Dynamical Systems in Population Biology, 2nd edn. Springer Nature, Switzerland (2017)
Acknowledgements
The work of the first two authors were supported by the National Natural Science Foundation of China (Nos. 12071434,12011530398). The work of the fourth author was partially supported by his NSERC discovery grant of Canada (Grant No. RGPIN2016-04709).
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Ma, M., Yue, J., Huang, Z. et al. Propagation Dynamics of Bistable Traveling Wave to a Time-Periodic Lotka-Volterra Competition Model: Effect of Seasonality. J Dyn Diff Equat 35, 1745–1767 (2023). https://doi.org/10.1007/s10884-022-10129-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10884-022-10129-2