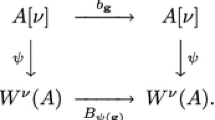Skip to main content
SpringerLink
Log in

Normal Forms for Equivariant Differential Equations

  • Published:
Journal of Dynamics and Differential Equations Aims and scope Submit manuscript

Abstract

We show that if the equation \(x'=A(t) x + f(t,x)\) is equivariant (respectively, reversible), then any normal form as well as the coordinate change taking the original equation to the normal form have equivariance (respectively, reversibility) properties. The proof depends on writing down somewhat explicit coordinate changes based on the block diagonalization of the linear part so that each block corresponds to a connected component of the nonuniform spectrum.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Barreira, L., Pesin, Ya.: Nonuniform Hyperbolicity. Dynamics of Systems with Nonzero Lyapunov Exponents, Encyclopedia of Mathematics and its Applications, vol. 115, Cambridge University Press, Cambridge, (2007)

  2. Barreira, L., Valls, C.: Reversibility and equivariance in center manifolds of nonautonomous dynamics. Discrete Contin. Dyn. Syst. 18, 677–699 (2007)

    Article  MathSciNet  Google Scholar 

  3. Barreira, L., Valls, C.: Evolution families and nonuniform spectrum, Electron. J. Qual. Theory Differ. Equ. 2016, Paper No. 48, 13 pp

  4. Barreira, L., Valls, C.: Normal forms via nonuniform hyperbolicity. J. Differential Equations 266, 2175–2213 (2019)

    Article  MathSciNet  Google Scholar 

  5. Field, M.: Equivariant dynamical systems. Trans. Amer. Math. Soc. 259, 185–205 (1980)

    Article  MathSciNet  Google Scholar 

  6. Georgi, M.: Bifurcations from homoclinic orbits to non-hyperbolic equilibria in reversible lattice differential equations. Nonlinearity 21, 735–763 (2008)

    Article  MathSciNet  Google Scholar 

  7. Gritsans, A.: Asymptotically stable heteroclinic cycles in discrete-time \(\mathbb{Z}_4\)-equivariant cubic dynamical systems. J. Difference Equ. Appl. 26, 1247–1265 (2020)

    Article  MathSciNet  Google Scholar 

  8. Guo, L.: Bifurcation analysis on a class of \(\mathbb{Z}_2\)-equivariant cubic switching systems showing eighteen limit cycles. J. Differential Equations 266, 1221–1244 (2019)

    Article  MathSciNet  Google Scholar 

  9. Guysinsky, M.: The theory of non-stationary normal forms. Ergodic Theory Dynam. Systems 22, 845–862 (2002)

    Article  MathSciNet  Google Scholar 

  10. Guysinsky, M., Katok, A.: Normal forms and invariant geometric structures for dynamical systems with invariant contracting foliations. Math. Res. Lett. 5, 149–163 (1998)

    Article  MathSciNet  Google Scholar 

  11. Haragus, M., Iooss, G.: Local Bifurcations, Center Manifolds, and Normal Forms in Infinite-Dimensional Dynamical Systems. Universitext. Springer-Verlag London, London (2011)

    Book  Google Scholar 

  12. Homburg, A., Knobloch, J.: Multiple homoclinic orbits in conservative and reversible systems. Trans. Amer. Math. Soc. 358, 1715–1740 (2006)

    Article  MathSciNet  Google Scholar 

  13. Homburg, A., Lamb, J.: Symmetric homoclinic tangles in reversible systems. Ergodic Theory Dynam. Systems 26, 1769–1789 (2006)

    Article  MathSciNet  Google Scholar 

  14. Liu, C.: The cyclicity of period annuli of a class of quadratic reversible systems with two centers. J. Differential Equations 252, 5260–5273 (2012)

    Article  MathSciNet  Google Scholar 

  15. Katok, A., Spatzier, R.: Differential rigidity of Anosov actions of higher rank abelian groups and algebraic lattice actions. Proc. Steklov Inst. Math. 216, 287–314 (1997)

    MathSciNet  MATH  Google Scholar 

  16. Lamb, J., Roberts, J.:Time-reversal symmetry in dynamical systems: a survey, in Time-Reversal Symmetry in Dynamical Systems (Coventry, 1996), Phys. D 112, 1–39 (1998)

  17. Mielke, A.: Hamiltonian and Lagrangian Flows on Center Manifolds. With Applications to Elliptic Variational Problems, Lecture Notes in Mathematics, vol. 1489, Springer-Verlag, Berlin, (1991)

  18. Roberts, J., Quispel, R.: Chaos and time-reversal symmetry. Order and chaos in reversible dynamical systems. Phys. Rep. 216, 63–177 (1992)

    Article  MathSciNet  Google Scholar 

  19. Sacker, R., Sell, G.: A spectral theory for linear differential systems. J. Differential Equations 27, 320–358 (1978)

    Article  MathSciNet  Google Scholar 

  20. Schwenker, S.: Generic steady state bifurcations in monoid equivariant dynamics with applications in homogeneous coupled cell systems. SIAM J. Math. Anal. 50, 2466–2485 (2018)

    Article  MathSciNet  Google Scholar 

  21. Sevryuk, M.: Reversible Systems. Lecture Notes in Mathematics, vol. 1211. Springer-Verlag, Berlin (1986)

  22. Sevryuk, M.: Herman’s approach to quasi-periodic perturbations in the reversible KAM context 2. Mosc. Math. J. 17, 803–823 (2017)

    Article  MathSciNet  Google Scholar 

  23. Siegmund: Normal forms for nonautonomous differential equations. J. Differential Equations 178, 541–573 (2002)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Departamento de Matemática, Instituto Superior Técnico, Universidade de Lisboa, 1049-001, Lisboa, Portugal

    Luis Barreira & Claudia Valls

Authors
  1. Luis Barreira
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Claudia Valls
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Luis Barreira.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supported by FCT/Portugal through the project UID/MAT/04459/2019.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Barreira, L., Valls, C. Normal Forms for Equivariant Differential Equations. J Dyn Diff Equat 34, 1371–1392 (2022). https://doi.org/10.1007/s10884-021-10006-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10884-021-10006-4

Keywords

Mathematics Subject Classification

Search

Navigation