Skip to main content
SpringerLink
Log in

Periodic Klein–Gordon Chains with Three Particles in 1:2:2 Resonance

  • Published:
Journal of Dynamics and Differential Equations Aims and scope Submit manuscript

Abstract

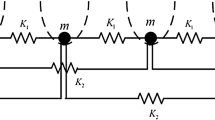
In this paper, we deal with the three degrees of freedom Hamiltonian systems describing the Klein–Gordon chains with three particles of equal masses and periodic boundary conditions. Specially, we focus on the case that the frequencies of the linearization are in 1 : 2 : 2 resonance. After second normalization the truncated normal form gives rise to an integrable system. Also, we calculate the coefficients of the terms that remain in normal form. Considering perturbation in frequencies, we analyze the dynamical features of this one degree of freedom system on the reduced phase space by calculating its equilibria and bifurcations. Specifically supercritical and subcritical Hamiltonian pitchfork bifurcations are found in different scenarios of parameters.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Arnol’d, V.I., Kozlov, V.V., Neishtadt, A.I.: Mathematical aspects of classical and celestial mechanics. In: Dynamical Systems III (ed. V.I. Arnol’d). Encyc. Math. Sciences. Springer (2006)

  2. Bruggeman, R., Verhulst, F.: Near-integrability and recurrence in FPU chains with alternating masses. J. Nonlinear Sci. 29, 183–206 (2019)

    Article  MathSciNet  Google Scholar 

  3. Christov, O.: Near-integrability of periodic Klein-Gordon lattices. Symmetry 11, 475 (2019)

    Article  Google Scholar 

  4. Dmitriev, S.V., Kevrekidis, P.G., Yoshikawa, N.: Discrete Klein–Gordon models with static kinks free of the Peierls–Nabarro potential. J. Phys. A Math. Gen. 38, 7617–7627 (2005)

    Article  MathSciNet  Google Scholar 

  5. Dmitriev, S.V., Kevrekidis, P.G., Yoshikawa, N.: Standard nearest-neighbour discretizations of Klein–Gordon models cannot preserve both energy and linear momentum. J. Phys. A Math. Gen. 39, 7217 (2006)

    Article  MathSciNet  Google Scholar 

  6. Hanßmann, H.: Local and semi-local bifurcations in hamiltonian dynamical systems—results and examples. Lecture Notes Math. 1893. Springer (2007)

  7. Hanßmann, H., Mazrooei-Sebdani, R., Verhulst, F.: The \(1:2:4\) resonance in a particle chain. Indagat. Math. New Ser. 32, 101–120 (2021)

    Article  MathSciNet  Google Scholar 

  8. Henrici, A., Kappeler, T.: Results on normal forms for FPU chains. Commun. Math. Phys. 278, 145–177 (2008)

    Article  MathSciNet  Google Scholar 

  9. Iooss, G., Pelinovsky, D.E.: Normal form for travelling kinks in discrete Klein–Gordon lattices. Physica D 216, 327–345 (2006)

    Article  MathSciNet  Google Scholar 

  10. Mazrooei-Sebdani, R., Hakimi, E.: Non-degenerate Hamiltonian Hopf bifurcations in \(\omega \) : \(3\) : \(6\) resonance (\(\omega =1\) or \(2\)). Regul. Chaotic Dyn. 25, 522–536 (2020)

    Article  MathSciNet  Google Scholar 

  11. Mazrooei-Sebdani, R., Hakimi, E.: On detuned \(1\) : \(1\) : \(3\) Hamiltonian resonance with cases of symmetric cubic and quartic potentials. Chaos 30, 093119 (2020)

    Article  MathSciNet  Google Scholar 

  12. Mazrooei-Sebdani, R., Yousefi, Z.: The coupled \(1\):\(2\) resonance in a symmetric case and parametric amplification model. Discrete Contin. Dyn. Syst. Ser. B 26, 3737–3765 (2021)

    MathSciNet  MATH  Google Scholar 

  13. Meyer, K.R.: Generic bifurcation in hamiltonian systems, pp. 62–70 in Dynamical Systems—Warwick 1974 (ed. A. Manning) LNM 468. Springer (1975)

  14. Morgan, A.M., Johansson, M., Kopidakis, G., Aubrya, S.: Standing wave instabilities in a chain of nonlinear coupled oscillators. Physica D 162, 53–94 (2002)

    Article  MathSciNet  Google Scholar 

  15. Pelinovsky, D., Sakovich, A.: Multi-site breathers in Klein–Gordon lattices: stability, resonances and bifurcations. Nonlinearity 25, 3423–3451 (2012)

    Article  MathSciNet  Google Scholar 

  16. Peyrard, M.: Nonlinear dynamics and statistical physics of DNA. Nonlinearity 17, R1–R40 (2004)

    Article  MathSciNet  Google Scholar 

  17. Poggi, P., Ruffo, S.: Exact solutions in the FPU oscillator chain. Physica D 103, 251–272 (1997)

    Article  MathSciNet  Google Scholar 

  18. Rink, B.: Symmetry and resonance in periodic FPU chains. Commun. Math. Phys. 218, 665–685 (2001)

    Article  MathSciNet  Google Scholar 

  19. Rink, B., Verhulst, F.: Near-integrability of periodic FPU-chains. Physica A 285, 467–482 (2000)

    Article  Google Scholar 

  20. Sanders, J.A., Verhulst, F., Murdock, J.: Averaging methods in nonlinear dynamical systems, Second Edition. Appl. Math. Sciences 59. Springer (2007)

  21. Sire, Y., James, G.: Travelling breathers in Klein–Gordon chains. C. R. Acad. Sci. Paris Ser. I 338, 661–666 (2004)

    Article  MathSciNet  Google Scholar 

  22. van der Aa, E., Verhulst, F.: Asymptotic integrability and periodic solutions of a Hamiltonian system in \(1:2:2\)-resonance. SIAM J. Math. Anal. 15, 890–911 (1984)

  23. Van der Meer, J.C.: On the geometry of Hamiltonian systems. Lecture notes, Technische Universiteit Eindhoven (2017)

  24. Verhulst, F.: Integrability and non-integrability of Hamiltonian normal forms. Acta Appl. Math. 137, 253–272 (2015)

    Article  MathSciNet  Google Scholar 

  25. Verhulst, F.: Recurrence and resonance in the cubic Klein–Gordon equation. Acta Appl. Math. 162, 145–164 (2019)

    Article  MathSciNet  Google Scholar 

  26. Wiggins, S.: Introduction to applied nonlinear dynamical systems and chaos, Second Edition. Text in Appl. Math. Springer (2003)

Download references

Acknowledgements

We deeply thank the suggestions and comments of the referees who contribute to the improvement in the clarity of the paper.

Author information

Authors and Affiliations

  1. Department of Mathematical Sciences, Isfahan University of Technology, Isfahan, 84156-83111, Iran

    Reza Mazrooei-Sebdani & Elham Hakimi

Authors
  1. Reza Mazrooei-Sebdani
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Elham Hakimi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Reza Mazrooei-Sebdani.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mazrooei-Sebdani, R., Hakimi, E. Periodic Klein–Gordon Chains with Three Particles in 1:2:2 Resonance. J Dyn Diff Equat 34, 1349–1370 (2022). https://doi.org/10.1007/s10884-021-10005-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10884-021-10005-5

Keywords

Mathematics Subject Classification

Search

Navigation