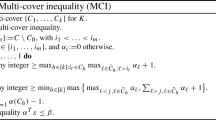Skip to main content

Advertisement

SpringerLink
Log in

Implicit cover inequalities

  • Published:
Journal of Combinatorial Optimization Aims and scope Submit manuscript

Abstract

In this paper we consider combinatorial optimization problems whose feasible sets are simultaneously restricted by a binary knapsack constraint and a cardinality constraint imposing the exact number of selected variables. In particular, such sets arise when the feasible set corresponds to the bases of a matroid with a side knapsack constraint, for instance the weighted spanning tree problem and the multiple choice knapsack problem. We introduce the family of implicit cover inequalities which generalize the well-known cover inequalities for such feasible sets and discuss the lifting of the implicit cover inequalities. A computational study for the weighted spanning tree problem is reported.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  • Aggarwal V, Aneja YP, Nair KPK (1982) Minimal spanning tree subject to a side constraint. Comput Oper Res 9:287–296

    Article  Google Scholar 

  • Agra A, Cerveira A, Requejo C, Santos E (2011) On the weight-constrained minimum spanning tree problem. In: Proceedings of the International Network Optimization Conference, volume 6701 of Lecture Notes in Computer Science, pp 156–161

  • Amado L, Bárcia P (1996) New polynomial bounds for matroidal knapsacks. Eur J Oper Res 95:201–210

    Article  MATH  Google Scholar 

  • Balas E, Jeroslow R (1972) Canonical cuts on the unit hypercube. SIAM J Appl Math 23:61–79

    Article  MathSciNet  MATH  Google Scholar 

  • Balas E (1975) Facets of the knapsack polytope. Math Programm 8:146–164

    Article  MathSciNet  MATH  Google Scholar 

  • Balas E, Zemel E (1978) Facets of the knapsack polytope from minimal covers. SIAM J Appl Math 34:119–148

    Article  MathSciNet  MATH  Google Scholar 

  • Camerini PM, Vercellis C (1984) The matroidal knapsack: a class of (often) well-solved problems. Oper Res Lett 3:157–162

    Article  MathSciNet  MATH  Google Scholar 

  • Crowder H, Johnson EL, Padberg MW (1983) Solving large-scale zero-one linear programming problems. Oper Res 31:803–835

    Article  MATH  Google Scholar 

  • Gu Z, Nemhauser GL, Savelsbergh MWP (1998) Lifted cover inequalities for 0–1 integer programs: Computation. INFORMS J Comput 10:427–437

    Article  MathSciNet  Google Scholar 

  • Gu Z, Nemhauser GL, Savelsbergh MWP (2000) Sequence independent lifting in mixed integer programming. J Combin Optim 10:109–129

    Article  MathSciNet  MATH  Google Scholar 

  • Hammer PL, Johnson EL, Peled UN (1975) Facets of regular 0–1 polytopes. Math Programm 8:179–206

    Article  MathSciNet  MATH  Google Scholar 

  • Hassin R, Levin A (2004) An efficient polynomial time approximation scheme for the constrained minimum spanning tree problem using matroid intersection. SIAM J Comput 33:261–268

    Article  MathSciNet  MATH  Google Scholar 

  • Henn ST (2007) Weight-constrained minimum spanning tree problem. Master’s thesis, University of Kaiserslautern, Kaiserslautern

  • Hong SP, Chung SJ, Park BH (2004) A fully polynomial bicriteria approximation scheme for the constrained spanning tree problem. Oper Res Lett 32:233–239

    Article  MathSciNet  MATH  Google Scholar 

  • Kaparis K, Letchford AN (2008) Local and global lifted cover inequalities for the 0–1 multidimensional knapsack problem. Eur J Oper Res 186:91–103

    Article  MathSciNet  MATH  Google Scholar 

  • Kaparis K, Letchford AN (2010) Separation algorithms for 0–1 knapsack polytopes. Math Programm 124:69–91

    Article  MathSciNet  MATH  Google Scholar 

  • Klabjan D, Nemhauser GL, Tovey C (1998) The complexity of cover inequality separation. Oper Res Lett 23:35–40

    Article  MathSciNet  MATH  Google Scholar 

  • Laurent M (1989) A generalization of antiwebs to independence systems and their canonical facets. Math Programm 45:97–108

    Article  MathSciNet  MATH  Google Scholar 

  • Martello S, Toth P (1990) Knapsack problems: algorithms and computer implementations. Wiley, Chichester

    MATH  Google Scholar 

  • Nemhauser GL, Wolsey LA (1988) Integer and combinatorial optimization. Wiley, New York

    Book  MATH  Google Scholar 

  • Pisinger D (2005) Where are the hard knapsack problems? Comput Oper Res 32:2271–2284

    Article  MathSciNet  MATH  Google Scholar 

  • Ravi R, Goemans MX (1996) The constrained minimum spanning tree problem. In: Proceedings of the Scandinavian Workshop on Algorithmic Theory, volume 1097 of Lecture Notes in Computer Science, pp 66–75

  • Requejo C, Agra A, Cerveira A, Santos E (2010) Formulations for the weight-constrained minimum spanning tree problem. In: Proceedings of the International Conference on Numerical Analysis and Applied Mathematics, volume 1281 of AIP Conference Proceedings, pp 2166–2169

  • Requejo C, Santos E (2011) Lagrangean based algorithms for the weight-constrained minimum spanning tree problem. In: Proceedings of the VII ALIO/EURO Workshop on Applied Combinatorial Optimization, pp 38–41

  • van Roy TJ, Wolsey LA (1987) Solving mixed integer programming problems using automatic reformulation. Oper Res 35:45–57

    Article  MathSciNet  MATH  Google Scholar 

  • Shogan A (1983) Constructing a minimal-cost spanning tree subject to resource constraints and flow requirements. Networks 13:169–190

    Article  MathSciNet  Google Scholar 

  • Wolsey LA (1975) Facets for a linear inequality in 0–1 variables. Math Programm 8:165–178

    Article  MathSciNet  MATH  Google Scholar 

  • Yamada T, Watanabe K, Kataoka S (2005) Algorithms to solve the knapsack constrained maximum spanning tree problem. Int J Comput Math 82:23–34

    Article  MathSciNet  MATH  Google Scholar 

  • Zemel E (1989) Easily computable facets of the knapsack polytope. Math Oper Res 14:760–765

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

Research partially funded by CIDMA (Centro de Investigação e Desenvolvimento em Matemática e Aplicações) through the FCT (Fundação para a Ciência e a Tecnologia) within project PEst-OE/MAT/UI4106/2014, and by FCT through program COMPETE: FCOMP-01-0124-FEDER-041898 within project EXPL/MAT-NAN/1761/2013.

Author information

Authors and Affiliations

  1. CIDMA and Department of Mathematics, University of Aveiro, Aveiro, Portugal

    Agostinho Agra & Cristina Requejo

  2. CIDMA, ISLA-Higher Institute of Leiria, Leiria, Portugal

    Eulália Santos

Authors
  1. Agostinho Agra
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Cristina Requejo
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Eulália Santos
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Agostinho Agra.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Agra, A., Requejo, C. & Santos, E. Implicit cover inequalities. J Comb Optim 31, 1111–1129 (2016). https://doi.org/10.1007/s10878-014-9812-3

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10878-014-9812-3

Keywords

Search

Navigation