Skip to main content
SpringerLink
Log in

How elementary prospective teachers use three fraction models: their perceptions and difficulties

  • Published:
Journal of Mathematics Teacher Education Aims and scope Submit manuscript

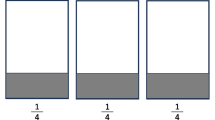
Abstract

This study is an examination of 79 elementary prospective teachers’ (PSTs’) capacity for recognizing the core ideas involved in modeling fraction addition problems and their difficulties in solving and presenting the process of fraction addition using area, length, and set models. PSTs completed a written task in which they represented the process of solving a set of fraction addition problems of varying complexity in terms of the sizes of the addends, the sums, and the denominators using the three models. The PSTs’ responses to the task were analyzed and clustered to identify the most salient and recurring patterns of erroneous approaches to modeling. While the PSTs recognized the core ideas involved in modeling fraction addition problems, their actual work samples demonstrated several areas for improvement. Some PSTs had invalid answers and representations that were indicative of their misunderstanding of key concepts. Some PSTs had correct answers, but their model did not support sense-making. Additionally, some PSTs’ representations did not clearly incorporate the salient properties of the area, length, and set models. Our analysis generated implications for mathematics teacher educators regarding what PSTs need to learn, develop further, unlearn, and refine in order to effectively teach uses of representation in elementary classroom.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  • Ball, D. L., & Forzani, F. M. (2009). The work of teaching and the challenge for teacher education. Journal of Teacher Education, 60(5), 497–511.

    Article  Google Scholar 

  • Ball, D. L., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching: What makes it special? Journal of Teacher Education, 59(5), 389–407.

    Article  Google Scholar 

  • Behr, M. J., & Post, T. R. (1992). Teaching rational number and decimal concepts. In T. R. Post (Ed.), Teaching mathematics in grades K-8: Research-based methods (2nd ed., pp. 201–248). Allyn and Bacon.

    Google Scholar 

  • Behr, M. J., Wachsmuth, I., & Post, T. (1988). Rational number learning aids: Transfer from continuous models to discrete models. Focus on Learning Problems in Mathematics, 10(4), 1–17.

    Google Scholar 

  • Cai, J. (2005). U.S. and Chinese teachers’ constructing, knowing, and evaluating representations to teach mathematics. Mathematical Thinking and Learning, 7(2), 135–169.

    Article  Google Scholar 

  • First Author. (2016).

  • Clements, D. H. (1999). “Concrete” manipulatives, concrete ideas. Contemporary Issues in Early Childhood, 1(1), 45–60.

    Article  Google Scholar 

  • Cramer, K., & Henry, A. (2002). Using manipulative models to build number sense for addition of fractions. In B. Litwiller & G. Bright (Eds.), Making sense of fractions, ratios, and proportions (pp. 41–48). National Council of Teachers of Mathematics.

    Google Scholar 

  • DeCuir-Gunby, J. T., Marshall, P. L., & McCulloch, A. W. (2011). Developing and using a codebook for the analysis of interview data: An example from a professional development research project. Field Methods, 23(2), 136–155.

    Article  Google Scholar 

  • Forzani, F. M. (2014). Understanding “core practices” and “practice-based” teacher education: Learning from the past. Journal of Teacher Education, 65(4), 357–368.

    Article  Google Scholar 

  • Grbich, C. (2013). Qualitative data analysis: An introduction (2nd ed.). Sage.

    Book  Google Scholar 

  • Grossman, P., Compton, C., Igra, D., Ronfeldt, M., Shahan, E., & Williamson, P. (2009). Teaching practice: A cross-professional perspective. Teachers College Record, 111(9), 2055–2100.

    Article  Google Scholar 

  • Hackenberg, A. J., & Lee, M. Y. (2015). Relationships between students’ fractional knowledge and equation writing. Journal for Research in Mathematics Education, 46(2), 196–243.

  • Hill, H. C., Ball, D. L., & Schilling, S. G. (2008). Unpacking pedagogical content knowledge: Conceptualizing and measuring teachers’ topic specific knowledge of students. Journal for Research in Mathematics Education, 39(4), 372–400.

    Article  Google Scholar 

  • Hodges, T. E., Cady, J., & Collins, R. L. (2008). Fraction representation: The not-so-common denominator among textbooks. Mathematics Teaching in the Middle School, 14(2), 78–84.

    Article  Google Scholar 

  • Huang, T., Liu, S., & Lin, C. (2009). Preservice teachers’ mathematical knowledge of fractions. Research in Higher Education Journal, 5, 1–8.

    Google Scholar 

  • Lamon, S. J. (2005). Teaching fractions and ratios for understanding: Essential content knowledge and instructional strategies for teachers (2nd ed.). Erlbaum.

    Google Scholar 

  • Lee, M. Y. (2017). Pre-service teachers’ flexibility with referent units in solving a fraction division problem. Educational Studies in Mathematics, 96(3), 327–348. https://doi.org/10.1007/s10649-017-9771-6

  • Lee, M. Y. (2019). A case study examining links between fractional knowledge and linear equation writing of seventh-grade students and whether to introduce linear equations in an earlier grade. International Electronic Journal of Mathematics Education, 14(1), 109–122. https://doi.org/10.12973/iejme/3980

  • Lee, M. Y. (2021). Using a technology tool to help pre-service teachers notice students’ reasoning and errors on a mathematics problem. ZDM – Mathematics Education, 53(1), 135–149. https://doi.org/10.1007/s11858-020-01189-z

  • Lee, M. Y., & Lee, J. (2019). Pre-service teachers’ perceptions of the use of representations and suggestions for students’ incorrect Use. Eurasia Journal of Mathematics, Science and Technology Education, 15(9), 1–21. https://doi.org/10.29333/ejmste/103055

  • Lee, J., & Lee, M. Y. (2020). Pre-service teachers’ exploration of model breaking points. International Journal of Science and Mathematics Education, 18, 549–575. https://doi.org/10.1007/s10763-019-09974-3

  • Lee, M. Y., & Lee, J. (2021a). Pre-service teachers’ selection, interpretation, and sequence of fraction examples. International Journal of Science and Mathematics Education, 19, 539–558. https://doi.org/10.1007/s10763-020-10062-0

  • Lee, M. Y., & Lee, J. (2021b). Spotlight on area models: Pre-service teachers’ ability to link fractions and geometric measurement. International Journal of Science and Mathematics Education, 19, 1079–1102. https://doi.org/10.1007/s10763-020-10098-2

  • Lee, J., & Dumitrascu, G. (2017). Preservice elementary teachers’ perceived preparedness of high-leverage practices in mathematics teaching. Education of Primary School Mathematics, 20(2), 153–162.

  • Lehrer, R. (2003). Developing understanding of measurement. In J. Kilpatrick, W. G. Martin, & D. Schifer (Eds.), A research companion to principles and standards for school mathematics (pp. 179–192). NCTM.

    Google Scholar 

  • Lo, J. J., & Luo, F. (2012). Prospective elementary teachers’ knowledge of fraction division. Journal of Mathematics Teacher Education, 15(6), 481–500.

    Article  Google Scholar 

  • Mack, N. K. (1995). Confounding whole-number and fraction concepts when building on informal knowledge. Journal for Research in Mathematics Education, 26(5), 422–441.

    Article  Google Scholar 

  • Martin, T., & Schwartz, D. L. (2005). Physically distributed learning: Adapting and reinterpreting physical environments in the development of fraction concepts. Cognitive Science, 29(4), 587–625.

    Article  Google Scholar 

  • McDonald, M., Kazemi, E., & Kavanagh, S. S. (2013). Core practices and pedagogies of teacher education: A call for a common language and collective activity. Journal of Teacher Education, 64(5), 378–386.

    Article  Google Scholar 

  • Mitchell, A. E. (2011). Interpreting students’ explanations of fraction tasks, and their connections to length and area knowledge (Doctoral dissertation). Australian Catholic University. https://doi.org/10.4226/66/5a961e7fc686c

    Book  Google Scholar 

  • National Governors Association Center for Best Practices & Council of Chief State School Officers. (2010). Common core state standards for mathematics. NGA & CCSSO.

  • National Mathematics Advisory Panel [NMAP]. (2008). The final report of the national mathematics advisory panel. Retrieved from http://www2.ed.gov/about/bdscomm/list/mathpanel/report/final-report.pdf

  • National Council of Teachers of Mathematics. (2014). Principles to actions: Ensuring mathematics success for all. NCTM.

  • Olanoff, D., Lo, J., & Tobias, J. (2014). Mathematical content knowledge for teaching elementary mathematics: A focus on fractions. The Mathematics Enthusiast, 11(2), 267–310.

    Article  Google Scholar 

  • Petit, M., Laird, R. E., & Marsden, E. L. (2010). A focus on fractions: Bringing research to the classroom. Taylor & Francis.

    Book  Google Scholar 

  • Rosli, R., Han, S., Capraro, R., & Capraro, M. (2013). Exploring preservice teachers’ computational and representational knowledge of content and teaching fractions. Journal of Korean Society of Mathematics Education, 17(4), 221–141.

    Google Scholar 

  • Second Author. (2015, 2017, 2019).

  • Shulman, L. S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15(2), 4–14.

    Article  Google Scholar 

  • Siegler, R. S., Thompson, C. A., & Schneider, M. (2011). An integrated theory of whole number and fractions development. Cognitive Psychology, 62(4), 273–296.

    Article  Google Scholar 

  • Son, J., & Lee, J. (2016). Preservice teachers’ understanding of fraction multiplication, representational knowledge, and computational skills. Mathematics Teacher Education and Development, 18(2), 5–28.

  • TeachingWorks. (n.d.). High-leverage content. Retrieved from http://www.teachingworks.org/work-of-teaching/high-leverage-content

  • Tirosh, D. (2000). Enhancing prospective teachers’ knowledge of children’s conceptions: The case of division of fractions. Journal for Research of Mathematics Education, 31(1), 5–25.

    Article  Google Scholar 

  • Usiskin, Z. (2007). Some thoughts about fractions. Mathematics Teaching in the Middle School, 12(7), 370–373.

    Article  Google Scholar 

  • van de Walle, J., Karp, K. S., & Bay-Williams, J. M. (2013). Elementary and middle school mathematics: Teaching developmentally (8th ed.). Pearson.

    Google Scholar 

  • Vig, R., Murray, E., & Star, J. R. (2014). Model breaking points conceptualized. Educational Psychology Review, 26, 73–90.

    Article  Google Scholar 

  • Watanabe, T. (2006). The teaching and learning of fractions: A Japanese perspective. Teaching Children Mathematics, 12(7), 368–374.

    Article  Google Scholar 

  • Zazkis, R., & Gadowsky, K. (2001). Attending to transparent features of opaque representations of natural numbers. In A. A. Cuoco & F. R. Curcio (Eds.), The roles of representation in school mathematics, 2001 yearbook (pp. 44–52). National Council of Teachers of Mathematics.

    Google Scholar 

  • Zhang, X., Clements, M. A., & Ellerton, N. F. (2015). Conceptual mis(understandings) of fractions: From area models to multiple embodiments. Mathematics Education Research Journal, 27, 233–261.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Oakland University, 456 Pioneer Drive, 485J Pawley Hall, Rochester, MI, 48309, USA

    Ji-Eun Lee

  2. Arizona State University, Tempe, AZ, USA

    Mi Yeon Lee

Authors
  1. Ji-Eun Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mi Yeon Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ji-Eun Lee.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lee, JE., Lee, M.Y. How elementary prospective teachers use three fraction models: their perceptions and difficulties. J Math Teacher Educ 26, 455–480 (2023). https://doi.org/10.1007/s10857-022-09537-4

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10857-022-09537-4

Keywords

Search

Navigation