A school-based professional development programme for teachers of mathematical modelling in Singapore

Abstract

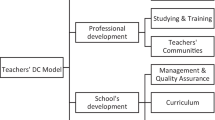
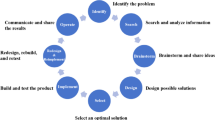
A school-based professional development programme (SBPD) aimed at developing secondary school mathematics teachers’ competencies to teach mathematical modelling in Singapore is presented and evaluated in this article. The SBPD is characterized by two key features—content elements to develop teachers’ knowledge and skills, and transformative learning cycles for teachers to elicit, enact and reorganize their orientations in a mathematical modelling classroom. Goal-based decision-making analysis of teachers’ practice suggests that this SBPD positively influences teachers’ knowledge and resources, goals and orientations in planning, designing and enacting modelling learning experiences.

Appendices

Appendix 1: Brief notes on level 2 modelling learning experience

Prior to the dart board game design task, Mr H had planned for students to be engaged in a level 2 modelling learning experience to construct a mathematical model for estimating the population of tree shrews in a nature reserve in Singapore. This is essentially a Fermi problem (Goldberger 1999) involving estimating a population, in this case, of tree shrews, based on mathematical reasoning. Students will have to apply proportional reasoning in formulating the estimation model for the population of tree shrews. Students needed to be familiar with the mathematical idea for this estimation model in formulating the expected pay-out of prizes for the dart board game design task.

Another focus of the Fermi problem task in estimating the population of tree shrews is to develop students’ modelling competency to make reasonable assumptions in the process of simplifying the model formulation. Mr H had intended for students to be competent in making assumptions for model formulation going into the dart board game design task. From the post-programme interview, Mr H commented that:

I think in the Fermi project rubrics, we already discussed about assumptions. So we came into the dart board game task without thinking about assumptions. We already know that assumptions need to be made.

Appendix 2: Lesson transcript Mr H

T: [Teacher gave out handouts for students to read through themselves for 2 min] Okay read through the handouts I gave you guys.

Ss: What are we doing?

T: I’ll explain everything in detail in another minute.

T: [after 1 min] Okay class, you are tasked to do something. You need to design a new dart board game for the school carnival. The objectives are you need to design a new dart board. There will be hundred rounds of games. You have a budget of about $100. This is not a strict restriction; you can change it if you want. You can charge any amount per game. And you can determine your own prizes. Finally, you must be profitable. You must make a profit. Any questions here before we continue? None okay.

T: This will be your final product. Your final product is to be a booklet, A4 size, maximum of 10 pages. With the following, you will need to have a scaled drawing of your design. You must have reasons why you design your dartboard and the reasons for the rules you have set for your dart board. The information on the cost, expenditure and the profit that you are expecting to have. And your bibliography.

T: So your project will be graded on the following. On the application of mathematical concepts, on the creativity of your design and the way you set your rules, and of course your presentation. The rubrics are at the last page of your handout. Take a look at it, I give you 1 min. Okay any questions? No, okay.

T: Now before we start on anything, we are going to have a class discussion. And this is on the second page of the handout. The two things that we need to consider is this. What is the main goal? And what is the useful mathematical relationship that we know to achieve that goal? So let’s have a look at the previous slides on objectives and restrictions.

To answer the question what is the main goal, in this case it would be? What’s the main goal for this particular project?

Ss: Must make profit.

T: Yes, it must be profitable. So you can state that the main goal for the review of this design is to make a profit. What do you know? You know that your budget is $100 or approximately $100. You know that you can charge any amount per game. You also know that you can determine your own prizes. In this case to make a profit, what would you think is the likely mathematical relationship that you are looking at? If you believe that profit is your goal, then how do you find profit then? How do you determine profit? Anyone?

S1: Something minus cost prize.

T: Something minus cost prize. What is that something? What is it equal to by the way?

S1: Equal to profit.

T: Hopefully. If we design the game well, then hopefully we get a profit. [T pointed to blank before minus sign] What is it that we are looking at here? Is it minus cost prize or cost prize minus?

Ss: Minus cost price.

T: [T pointed to blank before minus sign] So what is this again?

S2: Total money that you get

T: Total amount of money gained. So I’m going to introduce you another word which will encompass this phrase that you have coined. Total amount of money that you gain. In this case, that word will be revenue. So this will be the mathematical basis that we are going to work on. You must make sure that your revenue is more than your cost or expenditure to make a profit. So everything that we do is on the basis of this. [T pointed to the profit function, but students appeared to not understand this statement] How much revenue we are getting, minus away the cost or expenditure to get our profit. Any questions here? No okay, let’s move on to the next one.

T: For the next 10–15 min, I want you guys to consider when you are talking about the dart game that you are creating, I want you to discuss the factors that may affect the viability of the dart board design. In your groups now, 10–15 min, on the second page you have this table to fill in. Let’s talk about it and let’s fill in that table. So let’s do this.

S3: What is viability?

T: He’s asking what is viability. In this case, we are talking about the profitability of you dart board game. So what are the factors which will affect that?

T: [Teacher walked round the class]

T: [One group was not sure of what is to be discussed] Er, what affects? In this case it’s the profitability of the game. Okay? But limited to the prizes that you award, how much you charge per game and also the design of the board itself. So what are those factors there?

T: [T walked some distance away but still monitoring that group’s discussion]

[T walked over to that group again after hearing some responses from students] [Ss checking with T on whether some of their factors are similar] Yes, the board probability? And design also, yes? You think the probability will affect the design or the design will affect your probability?

S4: Must design dart board to make it difficult to win the grand prize.

T: Exactly, that’s one of your considerations for the design. Makes sense?

S5: [T moved to another group] How do you say the size of the part of the dart board as a factor?

T: You want to say the size of the angle of the sector in the dart board as one of the factor.

Would you want to consider any other shape? There are no restrictions on shapes.

T: [T moved to another group] Let’s see what you have here. The cost of prizes, chances of winning. Okay can you use these factors in your design?

S6: We give them very cheap prize.

T: The consideration is this. If you are giving them cheap prizes, will that be enough to draw them to your store? We can increase the chance of people coming to your store by making it more attractive to play.

T: [T moved to another group] You have three different dartboards, easy, medium and difficult. I need to succeed first, then I play more. If I fail, I need to pay more in order to get to the next level. Sounds complicated. Can you run through it again?

Ss: [Student explained game rules again]

T: Hah! Either I quit at the easy level or I move up to the next level, but I have to pay up. And the prize you get will be bigger, but the possibility will be less.

Interesting. How would you calculate the profit in this case?

Ss: [Student explained idea about base profit].

T: Oh, you are guaranteeing a profit of $50. How much more likely profit are you gaining above the $50? I would like to see you guys calculate it.

Ss: We are basing on the probability that one out of two people will want to pay to move up to the next level.

T: It’s a good idea. You’re giving them choice to move up the level with increasing difficulty level. But your problem would be when you are calculating the likely profit above the $50.

T: [T moved to another group] Your consideration is more towards reducing your expenditure. Are there anyways of reducing your expenditure, besides…?

Ss: [Students talk about how they can reduce the overheads by doing things themselves]

T: Physically, let’s talk. There are many ways. One way is how you set the rules of the game. Sorry this time round, we’re not talking about the expenditure, we’re talking about the revenue you’ll be getting. How can you get more revenue? How do you calculate your revenue? That’s the overall view. You might want to drill down to one individual game. How much profit are you to get from one individual game and how are you going to design your dartboard based on that formulae? So instead of worrying about expenditure, about trying to do things yourself instead of buying stuff.

T: [Teacher read through list of factors listed by students at another group].

What’s the most important factor here?

Hitting it and drop or hitting it and stick?

Ss: There’s a chance that it will stick.

T: It’s a consideration. Would it be easier to calculate the revenue and profit if you assume the dart will stick? Would it be easier if you throw the dart, it’ll stick. That means you will win. Would it be easier to calculate the probability? Should be. You may want to design the dartboard in a manner where it’s easier for you to calculate the probability. Okay. After that, this is my calculation of the profit. Now let’s see what happens when we put in the extra condition that it may drop off. If you assume the dart will stick and win, that means it is easier for you to calculate the profit. Can?

And as you mentioned, how many types of prizes, what are the regions? How large are the regions?

Ss: [Teacher moved to another group][Students were describing a complex dart board game design with spinning wheels].

T: How would you calculate the probability of the spinning wheel?

Appendix 3: Extract of students’ report on dart board game design artefact