Skip to main content

Characterizing pivotal teaching moments in beginning mathematics teachers’ practice

Journal of Mathematics Teacher Education volume 16, pages 125–147 (2013)Cite this article

Abstract

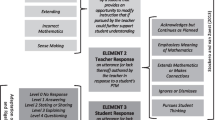
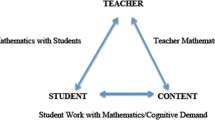
Although skilled mathematics teachers and teacher educators often “know” when interruptions in the flow of a lesson provide an opportunity to modify instruction to improve students’ mathematical understanding, others, particularly novice teachers, often fail to recognize or act on such moments. These pivotal teaching moments (PTMs), however, are key to instruction that builds on student thinking about mathematics. Video of beginning secondary school mathematics teachers’ instruction was analyzed to identify and characterize PTMs in mathematics lessons and to examine the relationships among the PTMs, the teachers’ decisions in response to them, and the likely impacts on student learning. These data were used to develop a preliminary framework for helping teachers learn to identify and respond to PTMs that occur during their instruction. The results of this exploratory study highlight the importance of teacher education preparing teachers to (a) understand the mathematical terrain their students are traversing, (b) notice high-leverage student mathematical thinking, and (c) productively act on that thinking. This preparation would improve beginning teachers’ abilities to act in ways that would increase their students’ mathematical understanding.

This is a preview of subscription content, access via your institution.

Access options

Buy single article

Instant access to the full article PDF.

USD 39.95

Price includes VAT (USA)
Tax calculation will be finalised during checkout.

References

  • Arafeh, S., Smerdon, B., & Snow, S. (2001, April). Learning from teachable moments: Methodological lessons from the secondary analysis of the TIMSS Video Study. Paper presented at the Annual Meeting of the American Educational Research Association, Seattle, WA.

  • Ball, D. L., & Cohen, D. K. (1999). Developing practice, developing practitioners: Toward a practice-based theory of professional education. In G. Sykes & L. Darling-Hammond (Eds.), Teaching as the learning profession: Handbook of policy and practice (pp. 3–32). San Francisco: Jossey Bass.

    Google Scholar 

  • Ball, D. L., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching: What makes it special? Journal of Teacher Education, 59(5), 389–407.

    Article  Google Scholar 

  • Berliner, D. C. (2001). Learning about and learning from expert teachers. International Journal of Educational Research, 35, 463–482.

    Article  Google Scholar 

  • Brousseau, G. (1997). Theory of didactical situations in mathematics: Didactique des mathematiques 1970–1990. Dordrecht, The Netherlands: Kluwer.

    Google Scholar 

  • Cengiz, N., Kline, K., & Grant, T. J. (2011). Extending students’ mathematical thinking during whole-group discussions. Journal of Mathematics Teacher Education, 14, 355–374.

    Article  Google Scholar 

  • Davies, N., & Walker, K. (2005, July). Learning to notice: One aspect of teachers’ content knowledge in the numeracy classrooms. In P. Clarkson, A. Downton, D. Gronn, M. Horne, A. McDonough, R. Pierce, & A. Roche (Eds.), Building connections: Theory research and practice. Proceedings of the 28th annual conference of the Mathematics Education Research Group of Australia, pp. 273–280. Sydney: MERGA.

  • Fennema, E., Carpenter, T. P., Franke, M. L., Levi, L., Jacobs, V. R., & Epson, S. B. (1996). A longitudinal study of learning to use children’s thinking in mathematics instruction. Journal for Research in Mathematics Education, 27, 403–434.

    Article  Google Scholar 

  • Horizon Research, Inc. (2000). Inside the classroom observation and analytic protocol. Chapel Hill, NC: Horizon Research, Inc.

  • Jacobs, V. R., Lamb, L. L. C., & Philipp, R. A. (2010). Professional noticing of children’s mathematical thinking. Journal of Research in Mathematics Education, 41(2), 169–202.

    Google Scholar 

  • Jaworski, B. (2004, July). Grappling with complexity: Co-learning in inquiry communities in mathematics teaching development. In M. J. Høines & A. B. Fuglestad (Eds.), Proceedings of the 28th Conference of the International Group for the Psychology of Mathematics Education. Vol 1, pp. 17–36. Bergen, Norway: Bergen University College.

  • Learning Mathematics for Teaching Project. (2011). Measuring the mathematical quality of instruction. Journal of Mathematics Teacher Education, 14, 25–47.

    Article  Google Scholar 

  • Leatham, K. R., Stockero, S. L., Peterson, B. E., & Van Zoest, L. R. (2011, October). Mathematically important pedagogical opportunities. In L. R. Wiest & T. Lamberg (Eds.), Proceedings of the 33rd Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, pp. 838–845. Reno, NV: University of Nevada, Reno.

  • Levin, D. M., Hammer, D., & Coffey, J. E. (2009). Novice teachers’ attention to student thinking. Journal of Teacher Education, 60(2), 142–154.

    Article  Google Scholar 

  • Luft, M., & Bemis, K. A. (1970, March). Video tape techniques for establishing inter-rater reliability. Paper presented at the Annual Meeting of the American Educational Research Association, Minneapolis, MN.

  • Mason, J. (1998). Enabling teachers to be real teachers: Necessary levels of awareness and structure of attention. Journal of Mathematics Teacher Education, 1, 243–267.

    Article  Google Scholar 

  • Mason, J. (2011). Noticing: Roots and branches. In M. G. Sherin, V. R. Jacobs, & R. A. Philipp (Eds.), Mathematics teacher noticing: Seeing through teachers’ eyes (pp. 35–50). New York: Routledge.

    Google Scholar 

  • National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: National Council of Teachers of Mathematics.

    Google Scholar 

  • Peterson, B. E., & Leatham, K. R. (2009). Learning to use students’ mathematical thinking. In L. Knott (Ed.), The role of mathematics discourse in producing leaders of discourse (pp. 99–128). Charlotte, NC: Information Age.

    Google Scholar 

  • Remillard, J. T., & Geist, P. K. (2002). Supporting teachers’ professional learning by navigating openings in the curriculum. Journal of Mathematics Teacher Education, 5, 7–34.

    Article  Google Scholar 

  • Rowland, T., Huckstep, P., & Thwaites, A. (2005). Elementary teachers’ mathematics subject knowledge: The knowledge quartet and the case of Naomi. Journal of Mathematics Teacher Education, 8, 255–281.

    Article  Google Scholar 

  • Santagata, R., & Guarino, J. (2011). Using video to teach future teachers to learn from teaching. ZDM, 43, 133–145.

    Article  Google Scholar 

  • Santagata, R., & van Es, E. A. (2010). Disciplined analysis of mathematics teaching as a routine of practice. In J. W. Lott & J. Luebeck (Eds.), AMTE Monograph 7: Mathematics teaching: Putting research into practice at all levels (pp. 109–123). San Diego, CA: Association of Mathematics Teacher Educators.

    Google Scholar 

  • Santagata, R., Zannoni, C., & Stigler, J. W. (2007). The role of lesson analysis in pre-service teacher education: An empirical investigation of teacher learning from a virtual video-based field experience. Journal of Mathematics Teacher Education, 10(2), 123–140.

    Article  Google Scholar 

  • Schoenfeld, A. H. (2011). How we think: A theory of goal-oriented decision making and its educational applications. New York: Routledge.

    Google Scholar 

  • Schön, D. A. (1983). The reflective practitioner: How professionals think in action. New York: Basic Books.

    Google Scholar 

  • Sherin, M. G. (2002). A balancing act: Developing a discourse community in a mathematics classroom. Journal of Mathematics Teacher Education, 5, 205–233.

    Article  Google Scholar 

  • Sherin, M. G., Jacobs, V. R., & Philipp, R. A. (Eds.) (2011). Mathematics teacher noticing: Seeing through teachers’ eyes. New York: Routledge.

    Google Scholar 

  • Silver, E. A., & Stein, M. K. (1996). The QUASAR Project: The “revolution of the possible” in mathematics instructional reform in urban middle schools. Urban Education, 30(4), 476–521.

    Article  Google Scholar 

  • Simons, D. J. (2000). Attentional capture and inattentional blindness. Trends in Cognitive Science, 4(4), 147–155.

    Article  Google Scholar 

  • SportsTec. (2010). Studiocode [Computer program]. Camarillo, CA: Vitigal Pty Limited.

    Google Scholar 

  • Stein, M. K., & Lane, S. (1996). Instructional tasks and the development of student capacity to think and reason: An analysis of the relationship between teaching and learning in a reform mathematics project. Educational Research and Evaluation, 2(1), 50–80.

    Article  Google Scholar 

  • Stein, M. K., Smith, M. S., Henningsen, M. A., & Silver, E. A. (2000). Implementing standards-based mathematics instruction: A casebook for professional development. New York: Teachers College Press.

    Google Scholar 

  • Stockero, S. L. (2008). Using a video-based curriculum to develop a reflective stance in prospective mathematics teachers. Journal of Mathematics Teacher Education, 11, 373–394.

    Article  Google Scholar 

  • Stockero, S. L. & Thomas, E. M. (in press). Transitions in prospective mathematics teacher noticing. In Proceedings of the 34th Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education.

  • Strauss, A., & Corbin, J. (1990). Basics of qualitative research: Grounded theory procedures and techniques. Newbury Park, CA: Sage Publications, Inc.

    Google Scholar 

  • Thompson, C., McCaughan, D., Cullum, N., Sheldon, T., & Raynor, P. (2004). Increasing the visibility of coding decisions in team-based qualitative research in nursing. International Journal of Nursing Studies, 41, 15–20.

    Article  Google Scholar 

  • van Es, E. A., & Sherin, M. G. (2002). Learning to notice: Scaffolding new teachers’ interpretations of classroom interactions. Journal of Technology and Teacher Education, 10(4), 571–596.

    Google Scholar 

  • van Es, E. A., & Sherin, M. G. (2008). Mathematics teachers’ “learning to notice” in the context of a video club. Teaching and Teacher Education, 24, 244–276.

    Article  Google Scholar 

  • Van Zoest, L. R., & Stockero, S. L. (2008). Concentric task sequences: A model for advancing instruction based on student thinking. In F. Arbaugh & P. M. Taylor (Eds.), AMTE Monograph 5: Inquiry into mathematics teacher education (pp. 47–58). San Diego, CA: Association of Mathematics Teacher Educators.

    Google Scholar 

  • Van Zoest, L. R., Stockero, S. L., & Kratky, J. L. (2010). Beginning mathematics teachers’ purposes for making student thinking public. Research in Mathematics Education, 12(1), 37–52.

    Article  Google Scholar 

  • Van Zoest, L. R., Stockero, S. L., & Taylor, C. E. (2011). The durability of professional and sociomathematical norms intentionally fostered in an early pedagogy course. Journal of Mathematics Teacher Education. doi:10.1007/s10857-011-9183-y.

  • Wagner, S., & Parker, S. (1993). Advancing algebra. In P. S. Wilson (Ed.), Research ideas for the classroom: High school mathematics (pp. 120–139). New York: Macmillan.

    Google Scholar 

  • Walshaw, M., & Anthony, G. (2008). The teacher’s role in classroom discourse: A review of recent research into mathematics classrooms. Review of Educational Research, 78(3), 516–551.

    Article  Google Scholar 

Download references

Acknowledgments

Data collection for the research reported here was supported in part by the US National Science Foundation under grant no. ESI-0243558, awarded to Judy Mumme and Nanette Seago, WestEd. The opinions expressed do not necessarily reflect the views of the Foundation. Data analysis was supported in part by Western Michigan University’s Faculty Research and Creative Activities Award and Michigan Technological University’s Research Excellence Fund—Research Seed Grant. The authors would like to thank James Kratky and Dolores Strom, Western Michigan University; Debra Kingdon, Michigan Technological University; and Cynthia Taylor, Millersville University, for their contributions to data collection and coding. Portions of this article were presented at the 2010 Annual Conference of the Psychology of Mathematics Education North American Chapter.

Author information

Authors and Affiliations

  1. Michigan Technological University, Houghton, MI, USA

    Shari L. Stockero

  2. Western Michigan University, Kalamazoo, MI, USA

    Laura R. Van Zoest

Authors
  1. Shari L. Stockero
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Laura R. Van Zoest
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shari L. Stockero.

Rights and permissions

Reprints and Permissions

About this article

Cite this article

Stockero, S.L., Van Zoest, L.R. Characterizing pivotal teaching moments in beginning mathematics teachers’ practice. J Math Teacher Educ 16, 125–147 (2013). https://doi.org/10.1007/s10857-012-9222-3

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10857-012-9222-3

  • Mathematics teacher education
  • Beginning teachers
  • Student thinking
  • Teachable moments
  • Teacher decisions