Introduction

Composites reinforced by high-strength synthetic fibers such as carbon fiber are widely used on airplanes, automobiles, etc., due to their high specific strength and modulus. However, these fibers are from nonrenewable resources. After their service life, these fibers are difficult to dispose and become potential threat to the environment. In contrast, natural fibers are extracted from renewable resources and are more eco-friendly. The big family of natural fibers includes plant fibers (wood or vegetable), and animal fibers such as silk [1, 2]. Commonly used high-strength natural fibers are bast fibers which include flax, jute, kenaf, and hemp fibers [3]. Compared to carbon and glass fibers, natural fibers bring about advantages including high specific mechanical properties, lower cost, sustainability, bio-degradability, and less environmental impact [4]. These characteristics explain why natural fibers and their composites have attracted attention from both the industry and academics. With the objective to reduce weight and cost, the automotive industry became the largest consumers of natural fiber composites. Natural fiber composites are used on structures such as door panels, seat backs, dashboard, pillar cover, engine insulation, headliner panel, and parcel shelves [5,6,7,8]. Natural fiber composites also have potential applications in construction industry [9], sport equipment [10], and other consumer products.

A composite is defined as a material made from two or more constituent materials which are separated and distinct within the composite system. The hybrid nature of composite materials usually adds to the difficulty in the prediction of their properties especially when complicated fiber architecture is involved. Due to continued efforts for several decades, both numerical and analytical models have been developed for the mechanical capability prediction of carbon and glass fibers. Review articles which summarized the latest simulation techniques for fiber-reinforced composites are also available in the literature with sufficient coverage [11, 12]. There are review works focusing on specific mechanical properties of composites. Nguyen et al. [13] reviewed the explicit finite element softwares for composite impact analysis. There are also analytical works and review articles dealing with particular composite structures. Thoppul et al. [14] reviewed the failure modes and failure prediction of mechanically fastened joints in polymer matrix composites. Simulation techniques for common phenomenon such as interfacial failure are also developed and reviewed [15].

However, research interests on natural fiber-reinforced composites happened much later in time than high-strength synthetic fibers. Relevant finite element models and analytical solutions specifically for the prediction of the mechanical properties of natural fiber composites are relatively limited in the reported studies. For instance, carbon fibers are normally considered as transversely isotropic material during finite element analysis [16]. Investigation carried out to observe the microstructure of flax fibers found a concentric multi-wall structure of elementary flax fiber [17]. However, due to lack of transverse properties, natural fibers were frequently modeled as isotropic material [18,19,20]. Sufficient attention should be paid on the systematic characterization of the mechanical properties of common natural fibers to fill the existing gap. In conclusion, continuous efforts are needed for the development of numerical and analytical models suitable for the prediction of the various behaviors of natural fiber composites before their practical applications.

With the recognition of the lack of relevant FE models for the prediction of the mechanical properties of polymers reinforced by natural fibers, the objective of this study is to simulate the progressive damage in natural fiber composites through finite element analysis. The material system under investigation is flax fiber/polypropylene composites. Both tensile and flexural behavior was considered. Coupons were fabricated from unidirectional flax tape and polypropylene film via compression molding. The developed (FEA) model started with micro-scale analyses which predicted the properties of unidirectional flax/polypropylene ply. Later, macro-scale analyses were carried out to predict the behavior of the coupon using the results of micro-scale analyses as inputs.

Experimental details

Unidirectional tapes of flax fibers (FLAXTAPE™ 110) supplied by Lineo Inc. were used as reinforcing fibers. The polymer resin used as matrix was thin film of polypropylene, which had a melt temperature of 195 °C. The flax fiber tapes and the polypropylene films were cut and stacked alternatively maintaining a fiber stacking sequence of [0/90/0/90/0/90/0]2. Prior to curing, the flax fiber tapes were dried in an oven at 85 °C for 2 h to remove possible moisture that might have been absorbed. The flax tapes and polypropylene films were later placed in a picture frame which had a geometry of 260 mm × 260 mm and cured through compression molding (Fig. 1a). The pressure applied during curing was 20 bar (2 MPa). The consolidation temperature and holding time were 195 °C and 10 min, respectively. The cured flax/polypropylene panels had a geometry of 260 mm × 260 mm × 2.31 mm. The densities of pure cured matrix (ρ m), composites (ρ c), and dry flax fibers (ρ f) were determined from measurements of weight and volume of samples. The fiber volume fraction, V f of the composite was 40%, determined from Eq. 1.

$$ \rho_{\text{c}} = V_{\text{f}} \rho_{\text{f}} + \left( {1 - V_{\text{f}} } \right)\rho_{\text{m}} $$
(1)
Figure 1
figure 1

Experimental details: a sample preparation process; b three-point bending test; c tensile test

Full size image

The cured flax/polypropylene panels were cut using water jet cutting to obtain coupons for three-point bending and tensile tests. The coupons for bending tests had a geometry of 130 mm × 13 mm × 2.31 mm. To remove any moisture that might have been introduced during cutting, specimens were heated at 60 °C for 24 h. ASTM D790 standard [21] was adopted for the bending test. An Instron 8801 universal testing machine was used to load specimens at a crosshead speed of 2 mm/min. The diameter of the loading roller (roller on the top surface) was 10 mm. The span was 80 mm (span-to-thickness ratio was approximately 32:1). Figure 1b shows a flax/polypropylene coupon under three-point bending test.

The coupons for tensile test had a geometry of 260 mm × 13 mm × 2.31 mm. The tensile test was performed using Instron 8501 at a testing speed of 2 mm/min, following ASTM D3039 recommendations [22]. An extensometer was attached to the sample to measure the strain. The gage length of the extensometer was 20 mm. Figure 1c shows a flax/polypropylene coupon under tensile test.

The single-fiber test was carried out using a micro-tester. The capacity of the load cell was 250 gf (around 2.45 N). Prior to the test, single-fiber was bonded using glue to a paper frame which had a circular hole at the center, as shown in Fig. 2. After the paper frame was clamped, the paper frame was cut at the center. The gage length was 11.5 mm. The testing rate was 0.003 mm/s.

Details of the multi-scale FEA model

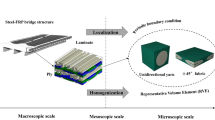
As mentioned above, the coupons consisted of unidirectional flax/polypropylene ply and had a stacking sequence of [0/90/0/90/0/90/0]2. The developed FEA model consisted of two steps. The first step was micro-scale analysis which predicted the properties of unidirectional flax/polypropylene ply using the properties of both constituents as inputs. The second step was macro-scale (Fig. 3) analysis which predicted the behavior of the entire coupon under bending or tensile loading conditions. The properties of the unidirectional flax/polypropylene ply were assigned to each ply of the coupon during macro-scale analysis. This modeling strategy is summarized in Fig. 3. During both micro- and macro-scale analysis, relevant failure criteria were selected to define the failures in the material. The simulation was completed using commercial FE software, ABAQUS, while the failure criteria were coded in USDFLD user subroutine through FORTRAN 77 programming language.

Figure 2
figure 2

Single-fiber experiment, (a) setup (b) clamped fiber in paper frame

Full size image
Figure 3
figure 3

Flowchart of multi-scale analyses

Full size image

Micro-scale analysis

Representative volume element (RVE) was constructed maintaining a fiber volume fraction of 40% (Fig. 3). In the current FE model, the flax fiber was treated as transversely isotropic material, while the polypropylene was considered as isotropic material with linear elastic behavior. The properties of the flax fibers and polypropylene used as inputs are summarized in Tables 1 and 2.

Table 1 Properties of flax fibers as inputs for micro-scale analysis [23, 24]
Full size table
Table 2 Properties of polypropylene as matrix resin [25,26,27]
Full size table

Both the matrix block and flax fiber were meshed using C3D4H 4-node linear tetrahedron elements (Fig. 4a). For the calculation of the homogenized elastic constants and the strength values of unidirectional flax/polypropylene ply, the periodic boundary conditions devised by Ji et al. [28] were adopted. The boundary condition for the prediction of longitudinal tensile properties is illustrated in Fig. 4b. In the micro-scale model, the maximum stress failure criterion was considered to be appropriate in describing the damage initiation in the flax fibers. It can be expressed as follows:

$$ \sigma_{\text{f}} \le X_{\text{fT}} \,(\sigma_{\text{f}} \ge 0)\,\,\quad{\text{or}}\,\quad - \sigma_{\text{f}} \le X_{\text{fC}} \,(\sigma_{\text{f}} < 0), $$
(2)

where X fT and X fC are the tensile and compressive strength, respectively; subscript ‘f’ represents the quantity of the fiber; and σ f is the normal stress component along the longitudinal direction of the fiber.

Figure 4
figure 4

Details of micro-scale analysis, a mesh applied (C3D4H element); b boundary condition for longitudinal tensile properties (along fiber direction)

Full size image

A modified von Mises criterion (the Stassi’s criterion) was employed to define the failure in the matric block. The Stassi’s criterion is expressed as follows:

$$ \left[ {\frac{1}{{X_{\text{mT}} }} - \frac{1}{{X_{\text{mC}} }}} \right]\left( {\sigma_{1} + \sigma_{2} + \sigma_{3} } \right) + \frac{1}{{X_{\text{mT}} }} \times \frac{1}{{X_{\text{mC}} }}\left\{ {\frac{1}{2}\left[ {\left( {\sigma_{1} - \sigma_{2} } \right)^{2} + \left( {\sigma_{2} - \sigma_{3} } \right)^{2} + \left( {\sigma_{3} - \sigma_{1} } \right)^{2} } \right]} \right\} \le 1 $$
(3)

or

$$ \left[ {\frac{1}{{X_{\text{mT}} }} - \frac{1}{{X_{\text{mC}} }}} \right]3P + \frac{1}{{X_{\text{mT}} }} \times \frac{1}{{X_{\text{mC}} }}\sigma_{\text{vm}}^{2} \le 1, $$
(4)

where σ 1, σ 2, and σ 3 are the principal stresses along the three principal directions. The term ‘P’ refers to the hydrostatic pressure and σ vm refers to the Von Mises stress components. X mT and X mC are the tensile and compressive strength of the matrix resin, where ‘m’ stands for the matrix resin.

Macro-scale analysis

The progressive damage analysis was performed during the macro-scale analysis to predict the tensile strength and bending behavior of flax/polypropylene composites. The damage initiation and subsequent material property degradation were simulated by using USDFLD user interface. The Hashin’s failure criteria in 3D form, which are failure criteria based on failure modes [29], were used for the analysis of each flax/polypropylene ply during macro-scale analysis.

Fiber failure in tension (σ 1 > 0):

$$ \left( {\frac{{\sigma_{1} }}{{X_{{{\text{ply}}T}} }}} \right)^{2} + \frac{{\tau_{12}^{2} + \tau_{13}^{2} }}{{\left( {S_{{{\text{ply}}12}} } \right)^{2} }} \le 0 $$
(5)

Fiber failure in compression (σ 1 < 0):

$$ |\sigma_{ 1} | \le X_{\text{plyC}} $$
(6)

Matrix failure in tension (σ 2 + σ 3 > 0):

$$ \left( {\frac{{\sigma_{2} + \sigma_{3} }}{{Y_{\text{plyT}} }}} \right)^{2} + \frac{{\tau_{23}^{2} - \sigma_{2} \sigma_{3} }}{{\left( {S_{{{\text{ply}}23}} } \right)^{2} }} + \frac{{\tau_{12}^{2} + \tau_{13}^{2} }}{{\left( {S_{{{\text{ply}}12}} } \right)^{2} }} \le 1 $$
(7)

Matrix failure in compression (σ 2 + σ 3 < 0):

$$ \left[ {\left( {\frac{{Y_{{{\text{ply}}C}} }}{{2S_{{{\text{ply}}23}} }}} \right)^{2} - 1} \right]\frac{{\sigma_{2} + \sigma_{3} }}{{Y_{{{\text{ply}}C}} }} + \left( {\frac{{\sigma_{2} + \sigma_{3} }}{{2S_{{{\text{ply}}23}} }}} \right)^{2} + \frac{{\tau_{23}^{2} - \sigma_{2} \sigma_{3} }}{{\left( {S_{{{\text{ply}}23}} } \right)^{2} }} + \frac{{\tau_{12}^{2} + \tau_{13}^{2} }}{{\left( {S_{{{\text{ply}}12}} } \right)^{2} }} \le 1 $$
(8)

where the ‘ply’ in the subscript represents the quantity of the unidirectional flax/polypropylene ply which is calculated by micro-scale analysis.

Results and discussion

Variation in material properties

Early reported research works on natural fiber composites have frequently led to the same conclusion that there might be high variation in the properties natural fibers and their composites. For natural fibers, such variation might be higher than carbon and glass fibers. However, for their composites, the extent of variation is often overestimated. Eight flax/polypropylene coupons were tested for their tensile properties and the results are summarized in Fig. 5. The results of the eight coupons tested show an acceptable consistency. The coefficient of variation for tensile strength of flax/polypropylene composites is 9.78%. It was reported that the coefficient of variation for the tensile strength of carbon fiber composites was 3.49% [30]. Such coefficient of variation for glass fiber composites was reported to be 6.93% [31]. The variation in tensile strength of flax fiber composites is only slightly higher than that of carbon and glass fiber composites. The results of three-point bending tests on flax/polypropylene composites are summarized in Fig. 6. The bending test results manifested a rather moderate variation in properties. The coefficient of variation for the peak flexure load was 6.82%. Natural fibers are commonly known to have relatively high variation in their properties. However, a natural fiber composite coupon or structure consists of numerous fibers. There is an averaging effect. Therefore, the variation in the properties of natural fiber composites is relatively moderate.

Figure 5
figure 5

Tensile test results of flax/polypropylene composites

Full size image
Figure 6
figure 6

Three-point bending test results of flax/polypropylene composites

Full size image

Micro-scale analysis

The micro-scale analysis was performed to predict the properties of unidirectional flax fiber/matrix composites by employing micro-scale RVE. Typical results of micro-scale analysis including both damage distribution and stress–strain curves are shown in Figs. 7 and 8. From Fig. 7a, the longitudinal modulus, E ply11, and longitudinal tensile strength, X plyT , can be obtained. The damage contours under longitudinal tensile loading, as shown in Fig. 7b, show that failure mainly initiated in the fiber. Under in-plane shear loading, failure is mainly observed in the matrix resin near the fiber as shown in Fig. 8b. The results of micro-scale analysis are summarized in Tables 3 and 4.

Figure 7
figure 7

Longitudinal tensile strength prediction of micro-scale RVE: a stress–strain curve; b damage contour

Full size image
Figure 8
figure 8

In-plane shear strength prediction of micro-scale RVE: a stress–strain curve; b damage contour

Full size image
Table 3 Elastic constants of a unidirectional flax/polypropylene ply predicted by micro-scale analysis (V f = 40%)
Full size table
Table 4 Strength values of a unidirectional flax/polypropylene ply predicted by micro-scale analysis (V f = 40%)
Full size table

The elastic constants of unidirectional flax/polypropylene ply predicted by micro-scale analysis will be assigned to each ply during macro-scale analysis. Analytically, these properties can be determined through the Chamis's equation [32] as

$$ E_{{{\text{ply}}11}} = V_{\text{f}} E_{{{\text{f}}11}} + (1 - V_{\text{f}} )E_{\text{m}} $$
(9)
$$ E_{{{\text{ply}}22}} = E_{{{\text{ply}}33}} = \frac{{E_{\text{m}} }}{{1 - \sqrt {V_{\text{f}} } \left( {1 - \frac{{E_{\text{m}} }}{{E_{{{\text{f}}22}} }}} \right)}} $$
(10)
$$ G_{{{\text{ply}}12}} = G_{{{\text{ply}}13}} = \frac{{G_{\text{m}} }}{{1 - \sqrt {V_{\text{f}} } \left( {1 - \frac{{G_{\text{m}} }}{{G_{{{\text{f}}12}} }}} \right)}} $$
(11)
$$ G_{{{\text{ply}}23}} = \frac{{G_{\text{m}} }}{{1 - \sqrt {V_{\text{f}} } \left( {1 - \frac{{G_{\text{m}} }}{{G_{{{\text{f}}23}} }}} \right)}} $$
(12)
$$ \upsilon_{\text{ply12}} = \upsilon_{{{\text{ply}}13}} = V_{\text{f}} \upsilon_{{{\text{f}}12}} + (1 - V_{\text{f}} )\upsilon_{\text{m}} $$
(13)
$$ \upsilon_{{{\text{ply}}23}} = \frac{{E_{{{\text{f}}22}} }}{{2G_{{{\text{f}}23}} }} - 1 $$
(14)

Table 3 shows that the elastic constants predicted by the micro-scale FE model were reasonably close to that calculated by Chamis's equation. The strength values of the unidirectional flax/polypropylene ply were predicted through the micro-scale FE model and are summarized in Table 4. These strength values would be used during programming of the USDFLD user subroutine for macro-scale analysis.

Tensile simulation of flax/polypropylene composites

Predictions of tensile behavior of flax/polypropylene composites from the developed FE model are compared against experimental results. As natural fibers generally display a wider scattering of properties compared to their synthetic counterparts, prediction of stiffness or slope of stress–strain response curve is considered reasonable (Fig. 9) compared to data collected from the experiments. The FE model predicts brittle failure which is similar to experimental observations noted in the previous section, where the predominant failure mode of tested coupons is characterized by a sudden major load drop of the composite laminate (Fig. 5). When fibers are stretched beyond their failure strain, they are ruptured resulting in catastrophic brittle failure of the laminates.

Figure 9
figure 9

Tensile stress–strain curves of unidirectional flax/polypropylene composites

Full size image

While failure mode and stiffness are predicted with reasonably good accuracy, discrepancies are noted in strength values. These are attributable to the assumption of linear behavior of natural fiber in the finite element model. In fact, a certain degree of nonlinearity is displayed by natural fibers as confirmed by our experiments on flax and glass fibers. Flax fibers, obtained from the same batch of unidirectional flax fiber tapes, were tested under tensile loading and their response, as shown in Fig. 10, is compared against that of glass fibers tested separately. The stress–strain behavior of glass fiber is linear up to the point of rupture, while flax fibers manifested a nonlinear tread up to failure, as shown in Fig. 9 which is a consequence of nonlinear tensile behavior of the natural fiber constituents arising from the presence of dislocations [33]. As the developed FEA model assumes linear elastic behavior of flax fibers, the nonlinear tensile response of flax fibers and their composites was not reflected in the predicted tensile stress–strain curve.

Figure 10
figure 10

Comparison between glass fibers and flax fibers in terms of their response under tensile loading

Full size image

Bending simulation of flax/polypropylene composites

In this study, the results of FEA analysis were compared with the experimental results to verify the accuracy of FEA model. The top and bottom surfaces of flax coupons after three-point bending test were observed. Damages were found on both top and bottom surfaces, as shown in Figs. 10d and 11b. These damages were successfully predicted by the FEA model. Fiber-dominated failure was predicted on both the top and bottom surfaces of the coupon, as shown in Fig. 11a, c.

Figure 11
figure 11

Damages on the top (a, b) and bottom (c, d) surfaces of flax/polypropylene composites after three-point bending

Full size image

The damage contours of the four damage modes expressed in Eqs. (5)–(8) are presented in Fig. 12. As shown in Fig. 12a, fiber tensile failure was mainly seen in 0° ply. Under bending load, there would be a tensile stress field near the bottom surface. Therefore, fiber tensile failure was observed at the bottom surface. Only fibers in the 0° ply were loaded in tensile along fiber direction. Therefore, fiber tensile failure was mainly observed in 0° ply near the bottom surface. Similarly, fiber failure in compression was observed in 0° ply near the top surface (Fig. 12b). Both matrix failure in tension and compression were observed as shown in Fig. 12c, d. When a load was applied transversely to fiber direction, matrix-dominated failure would be likely to occur. For 90° ply near the top and bottom surfaces, the load was applied transversely to fiber direction. Therefore, matrix-dominated failure was mainly observed in 90° ply near the top and bottom surfaces as shown in Fig. 12c, d.

Figure 12
figure 12

Damage contours for all the four failure modes considered: a fiber failure in tension (mainly in 0° ply near the bottom surface); b fiber failure in compression (mainly in 0° ply near the top surface); c matrix failure in tension (mainly in 90° ply near the bottom surface); d matrix failure in compression (mainly in 90° ply near the top surface)

Full size image

The simulated flexure load/flexure extension curve is plotted in Fig. 13 in comparison with that of experimental curve. The peak flexure load predicted by FE analysis was 59.4 N, while the average peak flexure load measured during experiments was 58.6 N. The peak flexure load was successfully predicted. As shown in Fig. 13, in general, the simulation curve matches well with the experiment curve. However, it is also evident that the simulated curve exhibited a more brittle behavior. As mentioned above, four failure modes are considered in the developed FEA model. Once the stress state satisfies any of the failure criteria, the stiffness of the material would be degraded accordingly. Consequently, the load would decrease. As shown in Fig. 13, the load begins to decrease after point ‘a.’ Damage states corresponding to points ‘a’ and ‘b’ were examined and the damage distribution due to fiber tensile failure is plotted in Fig. 14. As illustrated in Fig. 14, from point ‘a’ to point ‘b’ (correspondingly, the flexure extension increases from 4.9 to 5.5 mm), the extent of fiber failure in tension increased significantly. Therefore, the predicted load decreased as shown in the simulation curve. The developed FEA model successfully predicted the peak flexure load and the major failure modes. This modeling strategy is effective for natural fiber composites. However, further improvement needs to be included to better predict the progressive damages under mechanical loading.

Figure 13
figure 13

Flexural properties of flax/polypropylene composites

Full size image
Figure 14
figure 14

Progression of fiber failure in tension under bending load

Full size image

Conclusions

The mechanical properties of unidirectional flax fiber/polypropylene composites were experimentally studied. A FEA model based on progressive damage analysis was developed to predict both the tensile and flexure behavior of flax/polypropylene composites. The proposed FEA model started with micro-scale analysis which predicted the properties of unidirectional flax fiber/polypropylene ply with the properties of flax fiber and polypropylene as inputs. The results of micro-scale analysis were assigned to each ply during macro-scale analysis which predicted the properties of the composite coupons. The Hashin’s failure criteria in 3D form were adopted to define the failure in unidirectional flax/polypropylene ply during macro-scale analysis. The progressive damage analysis was carried out during both micro- and macro-scale analysis by using USDFLD user subroutine which included both failure criteria and subsequent material property degradation. The multi-scale FEA model developed in the current study is able to predict reasonably well the tensile strength, peak flexure load, as well as damage modes of flax fiber-reinforced polypropylene composites under three-point bending loading conditions.

This study also provides a new perspective toward the variation in the properties of natural fibers and their composites. Tensile and bending tests carried out in this study revealed that the flax/polypropylene composites had very consistent test results. While relatively high variation in the properties of natural fibers was commonly accepted, natural fiber composites may have more consistent properties.