Skip to main content
SpringerLink
Log in

Maximum Likelihood Robust Regression by Mixture Models

  • Published:
Journal of Mathematical Imaging and Vision Aims and scope Submit manuscript

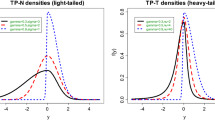
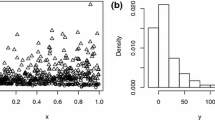
Abstract

In this paper, we will consider a robust estimator, which was proposed earlier by the authors, in a general non-linear regression framework. The basic idea of the estimator is, instead of trying to classify the observations to good and false, to model the residual distribution of the contaminants, determine the probability for each observation to be a good sample, and finally perform weighted fitting. The main contributions of this paper are: (1) We show now that the estimator is consistent with the true parameter values that simply means optimality regardless of the problematical outliers in the observations. (2) We propose how robust uncertainty computations and robust model selection can be performed in the similar, consistent manner. (3) We derive the expectation maximisation algorithm for the estimator and (4) extend the estimator to handle unknown outlier residual distributions. (5) We finally give some experiments with real data, where robustness in model fitting is needed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. H. Akaike, “On entropy maximization principle,” in (ed.), Applications of Statistics, P.R. Krishnaiah, North Holland, Amsterdam, pp. 27–41, 1977.

    Google Scholar 

  2. R. Beran, “Asymptotically efficient adaptive rank estimates in location models,” Ann. Stat. Vol. 2, No. 1, pp. 63–74, 1974.

    MATH  MathSciNet  Google Scholar 

  3. C. Biernacki, G. Celeux, and G. Govaert, “Strategies for getting the largest likelihood in mixture models,” Presented at the invited session in Joint Statistical Meetings 2000, Indianapolis. Presentation available at http://www.inrialpes.fr/is2/people/celeux/, 2000.

  4. S. Brandt, “Maximum likelihood robust regression with known and unknown residual models,” in Proc of the Statistical Methods in Video Proc Workshop, in conjunction with ECCV 2002, Copenhagen, Denmark, 2002a, pp. 97–102.

  5. S. Brandt, “Theorems and algorithms for multiple view geometry with applications to electron tomography,” Doctoral thesis, Helsinki University of Technology, 2002b.

  6. S. Brandt and J. Heikkonen, “A Bayesian weighting principle for the fundamental matrix estimation,” Pattern Recognit. Lett. Vol. 21, No. 12, pp. 1081–1092, 2000.

    Article  MATH  Google Scholar 

  7. S. Brandt and J. Heikkonen, “Optimal method for the affine F-matrix and its uncertainty estimation in the sense of both noise and outliers,” in Proc. of the Eighth International Conference on Computer Vision, Vol. 2, Vancouver, Canada, 2001, pp. 166–173.

  8. G. Celeux and J. Diebolt, “The SEM algorithm: A probabilistic teacher algorithm derived from the EM algorithm for the mixture problem,” Computat. Stat. Quart, Vol. 2, pp. 73–82, 1985.

    Google Scholar 

  9. G. Celeux and G. Govaert, “A classification EM algorithm for clustering and two stochastic versions,” Computat. Stat. Data Anal, Vol. 14, pp. 315–332, 1992

    Article  MATH  MathSciNet  Google Scholar 

  10. G. Csurka, C. Zeller, Z. Zhang, and O.D. Faugeras, “Characterizing the uncertainty of the fundamental matrix,” Comput. Vis. Image Underst, Vol. 68, No. 1, pp. 18–36, 1997

    Article  Google Scholar 

  11. A.P. Dempster, N.M. Laird, and D.B. Rubin, “Maximum likelihood form incomplete data via the EM algorithm (with discussion),” J.R. Statist. Soc. Ser. B-Stat. Methodol, Vol. 39, pp. 1–38, 1977.

    MATH  MathSciNet  Google Scholar 

  12. M. Fischler and L. Bolles, “Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography,” Commun. ACM, Vol. 24, pp. 381–385, 1981.

    Article  MathSciNet  Google Scholar 

  13. C. Fraley and A.E. Raftery, “How many clusters? which clustering method? answers via model-based cluster analysis,” Comput. J, Vol. 41, pp. 578–588, 1998.

    Article  MATH  Google Scholar 

  14. G.H. Golub and C.F.V. Loan, Matrix Computations, Second edn. The John Hopkins University Press, Chap. 7, 1989, pp. 345–346.

  15. R. Hartley and A. Zisserman, Multiple View Geometry in Computer Vision, Cambridge University Press, 2000.

  16. R.V. Hogg, “Adaptive robust procedures: A partial review and some suggestions for future applications and theory,” J. Am. Stat. Assoc, Vol. 69, No. 348, pp. 909–927, 1974.

    Article  MATH  MathSciNet  Google Scholar 

  17. P.J. Huber, Robust Statistics, Wiley, 1981.

  18. INRIA Syntim Project, http://www-syntim.inria.fr/syntim/analyse/paires-eng.html. 1999.

  19. H. Longuet-Higgins, “A computer algorithm for reconstructing a scene from two projections,” Nature, Vol. 293, pp. 133–135, 1981.

    Article  Google Scholar 

  20. Q.-T. Luong and O. Faugeras, “The fundamental matrix: Theory, algorithms, and stability analysis,” Int. J. Comput. Vis., Vol. 17, No. 1, pp. 43–76, 1996.

    Article  Google Scholar 

  21. G. McLachlan and T. Krishnan, The EM Algorithm and Extensions, Wiley, 1996.

  22. J. Rissanen, “Modeling by shortest data description,” Automatica, Vol. 14, pp. 465–471, 1978.

    Article  MATH  Google Scholar 

  23. J. Rissanen, “A universal prior for integers and estimation by minimum description length,” Ann. Stat., Vol. 11, No. 2, pp. 416–431, 1983.

    MATH  MathSciNet  Google Scholar 

  24. J. Rissanen, Stochastic Complexity in Statistical Inquiry, Vol. 15 of Series in Computer Science, World Scientific, Singapore, 1989.

    MATH  Google Scholar 

  25. P.J. Rousseeuw, “Least median of squares regression,” J. Am. Stat. Assoc., Vol. 79, pp. 871–880, 1984.

    Article  MATH  MathSciNet  Google Scholar 

  26. P.J. Rousseeuw and A.M. Leroy, Robust Regression and Outlier Detection, Wiley, 1987.

  27. J. Sacks, “An asymptotically efficient sequence of estimators of a location parameter,” Ann. Stat., Vol. 3, No. 2, pp. 285–298, 1975.

    MATH  MathSciNet  Google Scholar 

  28. Y. Sakamoto, M. Ishiguro, and G. Kitagawa, Akaike Information Criterion Statistics, KTK Scientific Publishers, 1986.

  29. G. Schwarz, “Estimating the dimension of a model,” Ann. Stat., Vol. 6, No. 2, pp. 461–464, 1978.

    MATH  Google Scholar 

  30. L. Shapiro and J. Brady, “Rejecting outliers and estimating errors in an orthogonal regression framework,” Philos. Trans. R. Soc. Lond. Ser. A-Math. Phys. Eng. Sci., Vol. 350, 1995.

  31. L. Shapiro, A. Zisserman, and M. Brady, “Motion from point matches using affine epipolar geometry,” in Proceedings of the Third European Conference on Computer Vision, 1994.

  32. M. Srinath, P. Rajasekaran, and R. Viswanathan, Introduction to Statistical Signal Processing with Applications, Prentice Hall, Chap. 5, 1996, pp. 146–149.

  33. C.J. Stone, “Adaptive maximum likelihood estimators,” Ann. Stat., Vol. 3, No. 2, pp. 267–284, 1975.

    MATH  Google Scholar 

  34. P. Torr and D. Murray, “The development and comparison of robust methods for estimating the fundamental matrix,” Int. J. Comput. Vis., Vol. 24, No. 3, pp. 271–300, 1997.

    Article  Google Scholar 

  35. P. Torr and A. Zisserman, “MLESAC: A new robust estimator with application to estimating image geometry,” Comput. Vis. Image Underst, Vol. 78, No. 1, pp. 138–156, 2000.

    Article  Google Scholar 

  36. V.N. Vapnik, The Nature of Statistical Learning Theory, Second edn., Springer-Verlag, New York, 2000.

    MATH  Google Scholar 

  37. J. Weng, T.S. Huang, and N. Ahuja, “Motion and structure from two perspective views: Algorithms, error analysis, and error estimation,” IEEE Trans. Pattern Anal. Mach. Intell., Vol. 11, No. 5, pp. 451–476, 1989.

    Article  Google Scholar 

  38. C.J. Wu, “On the convergence properties of the EM algorithm,” Ann. Stat, Vol. 11, No. 1, pp. 95–103, 1983.

    MATH  Google Scholar 

  39. G. Xu and Z. Zhang, Epipolar Geometry in Stereo, Motion and Object Recognition, Vol. 6 of Computational Imaging and Vision, Kluwer Academic Publishers, 1996.

  40. Z. Zhang, R. Deriche, O. Faugeras, and Q. Luong, “A robust technique for matching two uncalibrated images through the recovery of the unknown epipolar geometry,” Artif. Intell., Vol. 78, pp. 87–119, 1994.

    Article  MATH  Google Scholar 

  41. Z. Zhang and C. Loop, “Estimating the fundamental matrix by transforming image points in protective space,” Comput. Vis. Image Underst, Vol. 82, pp. 174–180, 2001.

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Laboratory of Computational Engineering, Helsinki University of Technology, P.O. Box 9203, FIN 02015 TKK, Finland

    Sami S. Brandt

Authors
  1. Sami S. Brandt
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sami S. Brandt.

Additional information

Sami Brandt received the degree of Master of Science in Technology from the department of Engineering Physics and Mathematics in Helsinki University of Technology, Finland, in September 1999 and the degree of Doctor of Science in Technology at the Laboratory of Computational Engineering, Helsinki University of Technology, in October 2002. After serving one year as a research scientist in Instrumentarium Corporation Imaging Division and two years as a post-doc at LCE, he is currently jointly affiliated at LCE and Information Processing Laboratory, University of Oulu, Finland; and he focuses research on bio-medical imaging and 3D vision. He is a member of the IEEE and IEEE Computer Society, member of the Pattern Recognition Society of Finland, member of the International Association for Pattern Recognition (IAPR), and member of the Finnish Inverse Problems Society.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Brandt, S.S. Maximum Likelihood Robust Regression by Mixture Models. J Math Imaging Vis 25, 25–48 (2006). https://doi.org/10.1007/s10851-005-4386-4

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10851-005-4386-4

Keywords

Search

Navigation