Abstract
Intertheoretic relations are an important topic in the philosophy of science. However, since their classical discussion by Ernest Nagel, such relations have mostly been restricted to relations between pairs of theories in the natural sciences. This paper presents a case study of a new type of intertheoretic relation that is inspired by Montague’s analysis of the linguistic syntax-semantics relation. The paper develops a simple model of this relation. To motivate the adoption of our new model, we show that this model extends the scope of application of the Nagelian (or related) models and that it shares the epistemological advantages of the Nagelian model. The latter is achieved in a Bayesian framework.










Similar content being viewed by others
Notes
The investigated theory-pairs include classical genetics and molecular genetics (or biochemistry), ecology and molecular biology, psychology and computational neuroscience, and macroeconomics and microeconomics.
We will see that there, in fact, are models of intertheory relations in linguistics. However, since these models only play a peripheral role in linguistic practice, they are rarely explicitly discussed.
For many years, Nagelian reduction has been considered a dead end. The present paper rejects this assumption. This stance is motivated by the observation (recorded in Dizadji-Bahmani et al. 2010) that Schaffner (1974) revised model of Nagelian reduction overcomes the problems of Nagel’s original model. For the present purposes, it will suffice to focus only on the Nagelian model. We outline a Schaffner-style extension of our model in Sect. 5.2.
The epistemic advantages of Nagelian reduction are shown in Dizadji-Bahmani et al. (2011).
The relevance of word order for the grammaticality of a sentence is a case in point.
Since syntax and semantics cover different target domains (see Sects. 1 and 2.2), they are often described as parts of the same theory, rather than as two distinct theories. Our choice of these two parts/theories is motivated by the fact that, in addition to formulating a formal theory of syntax and semantics, Montague’s framework already provides an analysis of their relation. This analysis facilitates the work of the philosopher of science, who is responsible for the construction of a model of this relation. Our choice of the syntax-semantics pair is further motivated by the understanding that the ready availability of an analysis of the syntax-semantics relation indicates the linguistic relevance of this (type of) relation.
Note that our discussion of the syntax-semantics relation regards syntax and semantics as linguistic theories. As a result, our insights into the syntax-semantics relation cannot be straightforwardly transferred to approaches to formalizing scientific theories (esp. to the syntactic vs. semantic view of scientific theories).
Thus, Montague (1976b) writes, “It is clear [\(\ldots \)] that [with the exception of Montague (1976a)] no adequate and comprehensive semantical theory has yet been constructed” (p. 222). Chomsky (1971) supports this claim by stating that “In the domain of semantics there are [\(\ldots \)] problems of fact and principle that have barely been approached, and there is no reasonably concrete or welldefined ‘theory of semantic representation’ to which one can refer” (p. 183).
Notably, the designators of semantic objects (which are terms of Montague’s logic IL) are not themselves linguistic expressions. In particular, since IL is (Henkin-)complete, the conflation of the language of IL and of natural language would trivialize our reductive endeavor.
As a result of this interpretation, distributional differences between common nouns and intransitive verbs can only be explained through syntax. Montague does not regard this delegation of explanatory power as a defect of his framework. To the contrary: He attributes “the fact that Ajdukiewicz’s proposals have not previously led to a successful syntax” to “the failure to pursue the possibility of syntactically splitting categories originally conceived in semantic terms” (see Montague 1976c, p. 249, fn. 4).
In particular, common nouns (e.g. man) combine with a determiner (e.g. the/a, interpreted as a function from properties of individuals to sets of such properties) to form a DP (here: the man/a man, interpreted as a set of properties of individuals) (see Montague 1976c, rules S2, S4; T2, T4).
Thus, this theory is concerned with the formation of complex linguistic expressions (e.g. sentences, clauses) from simpler expressions (e.g. individual words, phrases), and is supported by strings of expressions which reflect the assumed process for the formation of complex expressions.
We here understand ‘semantics’ as ‘compositional semantics’.
Admittedly, the type-checking role of syntax may already involve much of the (presumed) work of compositional semantics. This is illustrated by Kastner’s syntactic analysis of (ex.b) as (ex.c), whose subject DP (which is required for a successful type-check of the sentence) is obtained by applying the covert definite determiner \(\varDelta \) to a CP:
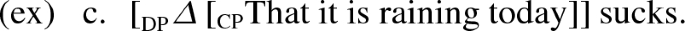
Our use of the terms phenomenological and fundamental is in accordance with the treatment of theories in physics. Our adoption of these terms in linguistics is motivated by the wish to avoid reference to the ‘reduced’ and the ‘reducing’ theory (see Sect. 1). Nothing more depends on this terminology.
We will see below that—because of the interpretation of bridge laws as statements about the inclusion relation between the extensions of terms of the two theories—the Nagelian model can, in fact, not be applied to the syntax-semantics pair. To allow a direct comparison of the Montagovian with the Nagelian model, we temporarily ignore this inapplicability.
To accommodate the word-order profiles of different languages (e.g. ‘subject-verb-object’ vs. ‘verb-subject-object’), we here use an order-invariant version,
 , of the concatenation operation \([~\cdot ~]\) from \({\mathbb {G}}_{\textsc {s}}\). The order-(in)variance of concatenation is discussed below and in Sect. 5.2.
, of the concatenation operation \([~\cdot ~]\) from \({\mathbb {G}}_{\textsc {s}}\). The order-(in)variance of concatenation is discussed below and in Sect. 5.2.This characterization of Nagelian bridge laws is due to Schaffner (1974, pp. 614–615) (see Schaffner 1993, pp. 411–477). However, since it generalizes Nagel’s categorization of bridge laws as meaning-entailments, conventional stipulations, or matters of fact (see Nagel 1961, pp. 354–355), we here treat it as a proper part of Nagel’s model.
Notably, Nagel himself only demands that bridge laws take the form of one-directional conditional statements (see Nagel 1961, pp. 354). The common conception of Nagelian bridge laws as biconditional statements can be attributed to the fact that all examples of bridge laws from Nagel (1961, Ch. 11) are biconditionals.
In virtue of this observation, Montague’s syntax-semantics relation is also not an instance of the interpretability relation between theories (see Tarski et al. 1953). This relation holds of two theories, \(T_{1}\) and \(T_{2}\), if there exists some extension, \(T_{1}^{*}\), of \(T_{1}\) via a recursive set of explicit definitions such that every consequence of \(T_{2}\) is a consequence of \(T_{1}^{*}\) (see Eberle 1971, p. 495).
Notably, relations between theories with different target domains may not be identified with heterogeneous reductions, whose constituent theories do not share the relevant predicates: Many heterogenous reductions (e.g. the reduction of thermodynamics to statistical mechanics) still have a common target domain (here: observable phenomena in macroscopic systems like gases).
To emphasize the weak nature of this relation w.r.t. reduction proper, we hereafter write reductive in scare quotes.
Bayesianism is presented and critically discussed in Earman (1992) and Howson and Urbach (2005). These texts also discuss Jeffrey conditionalization, which is an alternative updating rule. For an introduction to Bayesian epistemology, the reader is referred to Hájek and Hartmann (2010) and Hartmann and Sprenger (2010).
The restriction to singleton sets of rules (s.t. \(\mathbb {G} = \{\mathbb {G}_{\textsc {s}}\}\) and \(\mathbb {S} = \{\mathbb {S}_{\textsc {s}}\}\)) enables us to drop the subscript ‘s’ from \(G_{\textsc {s}}\) and \(S_{\textsc {s}}\).
We will hereafter abbreviate ‘\(1 - x\)’ as ‘\(\bar{x}\)’.
To ensure the comparability of the post-‘reductive’ situation from Sect. 4.2 with the post-reductive situation from Dizadji-Bahmani et al. (2011)—which assumes Schaffner’s (1967) revised model of Nagel Reduction (see Sect. 5.2)—, we let the posterior probability of the truth, \(\text {T}^{*}_{1}\), of the corrected version of the ‘fundamental’ proposition (given the truth, \(\text {T}_{1}\), or falsity, \(\lnot \text {T}_{1}\), of the ‘uncorrected’ fundamental proposition) and the truth, \(\text {T}_{2}\), of the uncorrected version of the ‘phenomenological’ proposition (given the truth, \(\text {T}^{*}_{2}\), or falsity, \(\lnot \text {T}^{*}_{2}\), of the corrected ‘phenomenological’ proposition) both be 1 (resp. 0).
Here, suitable is defined as ‘allowing the application of the described procedure for the establishment of the relevant intertheoretic relation’. As a result, suitable propositions for Nagelian reduction have a common target domain and contain surjectively related predicates.
The (syntactic and semantic) rules for the behavior of common nouns (see fn. 14.) are examples of such new rules.
A similar observation applies to syntactic categories (see Ajdukiewicz 1935).
Nagelian reduction can only derive a variant of this law, in which thermodynamic entropy does fluctuate in equilibrium.
Thus, (a) is strongly analogous to (b) if all members of \({\mathcal {E}}\) which are mentioned in (b) belong to an SVO-language and if (a) is the result of replacing all occurrences of
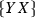 by occurrences of [XY].
by occurrences of [XY].
References
Ajdukiewicz, K. (1935). Die syntaktische Konnexität. Studia Philosophica, 1, 1–27.
Bach, E. (1976). An extension of classical transformational grammar. In R. Saenz (ed.), Proceedings of the 1976 conference Problems of Linguistic Metatheory (pp. 183–224). Michigan: Michigan State University.
Bartsch, R., & Vennemann, T. (1972). Semantic structures. Frankfurt: Athenäum.
Bickle, J. (2006). Reducing mind to molecular pathways: Explicating the reductionism implicit in current cellular and molecular neuroscience. Synthese, 151, 411–434.
Bovens, L., & Hartmann, S. (2003). Bayesian epistemology. Oxford: Clarendon Press.
Carnap, R. (1950). Empiricism, semantics, and ontology. Revue Internationale de Philosophie 4, 20–40; reprinted in Meaning and Necessity: a study in semantics and modal logic, The University of Chicago Press, Chicago and London (1988).
Carnap, R. (1968). Logische syntax der sprache. New York: Springer.
Chierchia, G., & Turner, R. (1988). Semantics and property theory. Linguistics and Philosophy, 11(3), 261–302.
Chomsky, N. (2000). Linguistics and brain science. In A. Marantz, Y. Miyashita, & W. O’Neil (Eds.), Image, language, brain. Cambridge, MA: MIT Press.
Chomsky, N., & Structure, D. (1971). Surface structure, and semantic representation. In D. Steinberg & L. Jakobovits (Eds.), Semantics: an interdisciplinary reader. Cambridge: Cambridge University Press.
Church, A. (1940). A formulation of the simple theory of types. Journal of Symbolic Logic, 5(2), 56–68.
Cresswell, M. J. (1973). Logics and languages. London: Methuen Young Books.
Darden, L., & Maull, N. (1977). Interfield theories. Philosophy of Science, 44(1), 43–64.
Dizadji-Bahmani, F., Frigg, R., & Hartmann, S. (2010). Who’s afraid of Nagelian reduction? Erkenntnis, 73(3), 393–412.
Dizadji-Bahmani, F., Frigg, R., & Hartmann, S. (2011). Confirmation and reduction: A Bayesian account. Synthese, 179(2), 321–338.
Earman, J. (1992). Bayes or bust?. Cambridge, MA: The MIT Press.
Eberle, R. A. (1971). Replacing one theory by another under preservation of a given feature. Philosophy of Science, 38(4), 486–501.
Eells, E., & Fitelson, B. (2000). Measuring confirmation and evidence. The Journal of Philosophy, 97(12), 663–672.
Fitelson, B. (1999). The plurality of Bayesian measures of confirmation and the problem of measure sensitivity. Philosophy of Science, 66, 362–378.
Forbes, G. (Forthcoming). Content and theme in attitude ascriptions. In A. Grzankowski & M. Montague (eds.), Non-propositional intentionality. Oxford: Oxford University Press.
Hájek, A., & Hartmann, S. (2010). Bayesian epistemology. In J. Dancy, E. Sosa, & M. Steup (Eds.), A companion to epistemology. Malden, MA: Blackwell Companions to Philosophy.
Hartman, J. (2012). Varieties of clausal complementation. Doctoral dissertation, Massachusetts Institute of Technology, Cambridge, MA.
Hartmann, S. (1999). Models and stories in hadron physics. In M. S. Morgan & M. Morrison (Eds.), Models as mediators (pp. 326–346). Cambridge: Cambridge University Press.
Hartmann, S., & Sprenger, J. (2010). Bayesian epistemology. In S. Bernecker & D. Pritchard (Eds.), Routledge companion to epistemology. Malden, MA: Routledge.
Hempel, C. G. (1966). Philosophy of natural science. Englewood Cliffs: Prentice-Hall.
Hendriks, H. (1990). Flexible Montague grammar. Amsterdam: ITLI Prepublication Series for Logic, Semantics and Philosophy of Language.
Hendriks, H. (1993). Studied flexibility: Categories and types in syntax and semantics. Doctoral dissertation, Institute for Logic, Language and Computation, Amsterdam.
Hoover, K. D. (2010). Idealizing reduction: The microfoundations of macroeconomics. Erkenntnis, 73(3), 329–347.
Howson, C., & Urbach, P. (2005). Scientific reasoning: The Bayesian approach. La Salle: Open Court.
Kastner, I. (2015). Factivity mirrors interpretation: The selectional requirements of presuppositional verbs. Lingua, 164(Part A), 156–188.
Kemeny, J. G., & Oppenheim, P. (1967). On reduction. Philosophical Studies, 19, 6–19.
Kuipers, T. A. F. (1982). The reduction of phenomenological to kinetic thermostatics. Philosophy of Science, 49(1), 107–119.
Levins, R., & Lewontin, R. (1980). Dialectics and reductionism in ecology. Synthese, 43, 47–78.
Lewis, D. (1970). General semantics. Synthese, 22(1–2), 18–67.
Litosseliti, L. (Ed.). (2010). Research methods in linguistics. London: Continuum.
Mitchell, S. D. (2003). Biological complexity and integrative pluralism. Cambridge: Cambridge University Press.
Montague, R. (1976a). English as a formal language. In R. H. Thomason (Ed.), Formal philosophy: Selected papers of Richard Montague. New Haven: Yale University Press.
Montague, R. (1976b). Universal grammar. In R. H. Thomason (Ed.), Formal philosophy: Selected papers of Richard Montague. New Haven: Yale University Press.
Montague, R. (1976c). The proper treatment of quantification in ordinary English. In R. H. Thomason (Ed.), Formal philosophy: Selected papers of Richard Montague. New Haven: Yale University Press.
Moortgat, M. (1997). Categorial type logics. In J. van Benthem & A. G. B. ter Meulen (Eds.), Handbook of logic and language. Amsterdam: Elsevier Science Publishers.
Nagel, E. (1961). The structure of science. London: Routledge and Kegan Paul.
Nagel, E. (1977). Teleology revisited. The Journal of Philosophy, 84, 261–301.
Neapolitan, R. (2003). Learning Bayesian networks. New York: Prentice Hall.
Partee, B. (1987). Noun phrase interpretation and type-shifting principles. In J. Groenendijk, D. de Jong, & M. Stokhof (Eds.), Studies in discourse representation theory and the theory of generalized quantifiers. Dordrecht: Foris Publications.
Partee, B. (1997). Montague grammar. In J. van Benthem & A. G. B. ter Meulen (Eds.), Handbook of logic and language (2nd ed.). Amsterdam: Elsevier Science Publishers.
Pearl, J. (1988). Probabilistic reasoning in intelligent systems: Networks of plausible inference. San Francisco: Morgan Kauffman.
Podesva, R. J., & Sharma, D. (Eds.). (2013). Research methods in linguistics. Cambridge: Cambridge University Press.
Poeppel, D., & Embick, D. (2005). Defining the relation between linguistics and neuroscience. In A. Cutler (Ed.), Twenty-first century psycholinguistics: Four cornerstones. Mahwah, NJ: Lawrence Erlbaum Associates.
Potts, C. (2002). The lexical semantics of parenthetical-as and appositive-which. Syntax, 5(1), 55–88.
Rasinger, S. M. (2013). Quantitative research in linguistics: An introduction. London: Bloomsbury.
Sag, I., Wasow, T., & Bender, E. (2003). Syntactic theory: A formal approach. Stanford: CSLI Publications.
Schaffner, K. F. (1967). Approaches to reduction. Philosophy of Science, 34, 137–147.
Schaffner, K. F. (1974). Reductionism in biology: Prospects and problems. In PSA: Proceedings of the biennial meeting of the philosophy of science association (pp. 613–632).
Schaffner, K. F. (1993). Discovery and explanation in biology and medicine. Chicago: Science and its Conceptual Foundations, The University of Chicago Press.
Schouten, M., & de Jong, H. L. (Eds.). (2012). The matter of the mind: Philosophical essays of psychology, neuroscience, and reduction. Oxford: Blackwell.
Takahashi, S. (2010). The hidden side of clausal complements. Natural Language and Linguistic Theory, 28(2), 343–380.
Tarski, A., Mostowski, A., & Robinson, R. M. (1953). Undecidable theories. Amsterdam: North-Holland.
Weber, M. (2005). Philosophy of experimental biology. Cambridge: Cambridge Studies in Philosophy and Biology, Cambridge University Press.
Acknowledgements
We wish to thank Lucas Champollion, Paul Egré, Branden Fitelson, Greg Novack, Peter Pagin, Jan Sprenger, Markus Werning, Rineke Verbrugge, and three anonymous reviewers for JoLLI for valuable input about the content of this paper. We owe our audiences at the Future of Philosophy of Science Conference, FEW 11, Bridges 2014, and the Tokyo Forum for Analytic Philosophy for many helpful comments and suggestions. The research for this paper has been supported by Tilburg University (via K. Liefke’s doctoral fellowship), the Alexander von Humboldt Foundation (via S. Hartmann’s Humboldt Professorship), and the German Research Foundation (via K. Liefke’s grant LI 2562/1-1).
Author information
Authors and Affiliations
Corresponding author
Appendix: Proofs and Calculations for Sect. 4
Appendix: Proofs and Calculations for Sect. 4
We have calculated the pre-‘reductive’ probabilities of the conjunction of the positive instantiations of S and G in Sect. 4.1. The joint distribution, \({{\varvec{P}}}_{2}(S, G, E)\), of the (post-‘reductive’) graph in Fig. 8 is given by the expression
Using the methodology from Bovens and Hartmann (2003), the prior probability of the conjunction of \({\text{ S }}\) and \({\text{ G }}\) is obtained as follows:
We yield the posterior probability, \({{\varvec{P}}}_{2}^{\,*} := {{\varvec{P}}}_{2}({\text{ S }}, {\text{ G }}|{\text{ E }})\), of the conjunction of \({\text{ S }}\) and \({\text{ G }}\) thus:
To obtain the difference \(\varDelta _{0}\), we calculate
This proves the following proposition:
Proposition 3
\(\varDelta _{0} = 0\) iff \(\sigma = 0\) or 1; \(\varDelta _{0} > 0\) iff \(\sigma \in (0, 1)\).
The difference, \(\varDelta _{1}\), between the conjunction’s pre- and post-‘reductive’ posterior probabilities is obtained as follows:
From the difference measure
we calculate the difference, \(\varDelta _{2}\), between the conjunction’s degree of confirmation before and after the establishment of Montague’s syntax-semantics relation as follows:
This completes our proofs and calculations for Sect. 4.
Rights and permissions
About this article
Cite this article
Liefke, K., Hartmann, S. Intertheoretic Reduction, Confirmation, and Montague’s Syntax-Semantics Relation. J of Log Lang and Inf 27, 313–341 (2018). https://doi.org/10.1007/s10849-018-9272-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10849-018-9272-8



 , of the concatenation operation
, of the concatenation operation  by occurrences of [XY].
by occurrences of [XY].