Green Alliances: Are They Beneficial when Regulated Firms are Asymmetric?

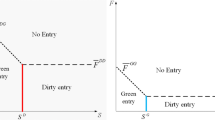
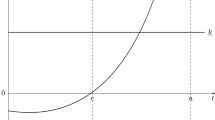
Abstract

In this paper, we analyze the collaboration between an environmental group (EG) and polluting firms when they are asymmetric in their abatement costs. We find that, as firms become more asymmetric, the EG collaborates more with the firm suffering from an abatement cost disadvantage, but this additional collaboration does not overcome firms’ cost asymmetry, producing an overall decrease in total abatement and an increase in total emissions. We also evaluate the welfare effects of introducing an EG and/or a regulator, finding that the latter generally yields larger welfare gains than the former when neither are present. Unlike previous studies, we show that the welfare benefit from a second agent is, under most settings, largest when firms are more asymmetric in their abatement costs.

A Appendix

1.1 A.1 Proof of Lemma 1

The first-order condition from the firm’s problem is

$$\begin{aligned} a+\lambda z_i -2q_i-q_j-t=0. \end{aligned}$$

Solving for $q_i$ we obtain firm i’s best response function,

$$\begin{aligned} q_i(q_j)=\frac{1}{2}[a+\lambda z_i-t]-\frac{1}{2}q_i. \end{aligned}$$

Firm j has a symmetric best response function. Simultaneously solving the best response functions for $q_i$ and $q_j$, we obtain equilibrium output in the fourth stage of,

$$\begin{aligned} q_i(t)=\frac{[a+\lambda (2z_i-z_j)]-t}{3}. \end{aligned}$$

We find that output is positive if and only if,

$$\begin{aligned} z_i>\frac{1}{2}z_j-\frac{a-t}{2\lambda }. \end{aligned}$$

Inserting equilibrium output in the firm’s fourth-stage profits, we find,

$$\begin{aligned} \pi _i(t)= & {} (a+\lambda z_i-q_i(t)-q_j(t))q_i(t)-t(q_i(t)-z_i)), \\= & {} \left( \frac{[a+\lambda (2z_i-z_j)]-t}{3}\right) ^2+tz_i,\\= & {} (q_i(t))^2+tz_i. \end{aligned}$$

1.2 A.2 Proof of Corollary 1

Taking a derivative of firm i’s profit with respect to $z_i$, $\lambda$, $z_j$, and t we obtain:

$$\begin{aligned} \frac{\partial \pi _i(t)}{\partial z_i}= & {} \frac{1}{9} (4 \lambda (a+2 \lambda z_i-\lambda z_j)+(9-4 \lambda ) t)>0,\\ \frac{\partial \pi _i(t)}{\partial \lambda }= & {} \frac{2}{9} (2 z_i-z_j) (a-t+2 \lambda z_i-\lambda z_j)>0,\\ \frac{\partial \pi _i(t)}{\partial z_j}= & {} -\frac{2}{9} \lambda (a-t+\lambda (2 z_i-z_j))<0,\\ \frac{\partial \pi _i(t)}{\partial t}= & {} -\frac{1}{9} (2( a- t)+4 \lambda z_i-9 z_i-2 \lambda z_j). \end{aligned}$$

The final comparative static is positive, $\frac{\partial \pi _i(t)}{\partial t}>0$, if $z_i<\frac{2(a-t-\lambda z_j)}{9-4\lambda }$.

1.3 Proof of Lemma 2

In the third stage, the regulator’s problem is,

$$\begin{aligned} \underset{t\ge 0}{\max }\, \frac{1}{2}[q_i(t)+q_j(t)]^2+[\pi _i(t)+\pi _j(t)]+t[q_i(t)+q_j(t)-Z]-d[q_i(t)+q_j(t)-Z]^2. \end{aligned}$$

The first-order condition is,

$$\begin{aligned} \frac{\partial SW}{\partial t}=\frac{2a(4d-1)-4t(1+2d)-Z[\lambda +4d(3-\lambda )]}{9} =0. \end{aligned}$$

Solving for t, we obtain the emission fee,

$$\begin{aligned} t=\frac{2a(4d-1)-Z[\lambda +4d(3-\lambda )]}{4(1+2d)}, \end{aligned}$$

in which $t(Z)>0$ if and only if $Z<\frac{2a(4d-1)}{\lambda +4d(3-\lambda )}\equiv \tilde{Z}$. The emission fee is unambiguously decreasing in aggregate abatement Z, and increasing in public image $\lambda$:

$$\begin{aligned} \frac{\partial t(Z)}{\partial Z}= & {} \frac{4 d (\lambda -3)-\lambda }{8 d+4}<0 \\ \frac{\partial t(Z)}{\partial \lambda }= & {} \frac{(4 d-1) Z}{8 d+4}>0. \end{aligned}$$

The comparative static on the emission fee with respect to environmental damage d is,

$$\begin{aligned} \frac{\partial t(Z)}{\partial d}=\frac{6 a+3 (\lambda -2) Z}{2 (2 d+1)^2}, \end{aligned}$$

which is positive if and only if $Z<\frac{2a}{2-\lambda }\equiv \bar{Z}$. Comparing $\bar{Z}$ and $\tilde{Z}$, we find that $\bar{Z}>\tilde{Z}$ under all parameter conditions:

$$\begin{aligned} \bar{Z}\equiv \frac{2a}{2-\lambda }>\frac{2a(4d-1)}{\lambda +4d(3-\lambda )}\equiv \tilde{Z}, \end{aligned}$$

which simplifies to $d>-\frac{1}{2}$, which always holds as $d>\frac{1}{2}$.

1.4 A.4 Proof of Lemma 3

In the second stage, we first evaluate realized equilibrium profits in the fourth stage $\pi _k(z_i,z_j)=\pi _k(t(Z))$, where t(Z) is from Lemma 2. Inserting this into each firm i’s problem in the second stage, we have that

$$\begin{aligned} \underset{z_i\ge 0}{\max } \, \pi _i(z_i,z_j)-\frac{1}{2}(\gamma _i-\theta b_i)(z_i)^2, \end{aligned}$$

and differentiating with respect to $z_i$ we find

$$\begin{aligned} \frac{a (8 d-2)+(4 d (\lambda -3)-\lambda ) (z_i+z_j)}{8 d+4}+ & {} \frac{(4 d (\lambda +1)+3 \lambda ) (2 a+4 d ((1+\lambda )z_i+(1-\lambda )z_j)+\lambda (3 z_i-z_j))}{8 (2 d+1)^2}\\+ & {} z_i (b_i \theta _i-\gamma _i)+\frac{z_i (4 d (\lambda -3)-\lambda )}{8 d+4}=0 \end{aligned}$$

Solving for $z_i$, we obtain firm i’s best response function

$$\begin{aligned} z_i(z_{j})=\frac{1}{A} \left[ 8 a d (4 d+\lambda +2)+6 a \lambda -4 a\right] -\frac{1}{A}[2 \lambda +(4 d+3) \left( \lambda ^2+4 d (2+\lambda (\lambda -1) )\right) ] z_{j}, \end{aligned}$$

where $A\equiv 16 d (5 d+3+2(d+1)(\gamma _i-b_i \theta ))+8( \gamma _i-b_i \theta )-(4 d+3)^2 \lambda ^2-32 d (2 d+1) \lambda +4 \lambda$, and $A>0$ if $\gamma _i>\frac{16 d^2 (\lambda -1) (\lambda +5)+8 d (\lambda (3 \lambda +4)-6)+\lambda (9 \lambda -4)}{8 (2 d+1)^2}$. Taking derivatives of A with respect to $\gamma _i$ and $\gamma _j$ yields

$$\begin{aligned} \frac{\partial A}{\partial \gamma _i}= & {} 8(1+2d)^2,\\ \frac{\partial A}{\partial \gamma _j}= & {} 0. \end{aligned}$$

Firm j has a symmetric best response function. This best response function has the following properties:

• 1. when $b_i=0$ and $\lambda =0$, the best response function is

  $$\begin{aligned} z_i(z_{j})=\frac{a \left( 8 d^2+4 d-1\right) -2 d (4 d+3) z_j}{2 \gamma _i+4 d (2 \gamma _i (d+1)+5 d+3)}, \end{aligned}$$

  which is unambiguously decreasing in $z_j$;

• 2. when $b_i=0$ and $\lambda >0$, the best response function is

  $$\begin{aligned} z_i(z_j)=\frac{8 a d (4 d+\lambda +2)+a(6 \lambda -4)-z_j\left[ (4 d+3) \left( 4 d ((\lambda -1) \lambda +2)+\lambda ^2\right) -2 \lambda \right] }{8 \gamma _i+16 d (2 \gamma _i (d+1)+5 d+3)-(4 d+3)^2 \lambda ^2-32 d (2 d+1) \lambda +4 \lambda }, \end{aligned}$$

  and is decreasing in $z_j$ if and only if $\gamma _i>\bar{\gamma }$;

• 3. when $b_i$, $\lambda >0$, $z_i(z_j)$ is decreasing in $z_j$ if and only if $\gamma _i>\bar{\gamma }+\theta b_i$,

where $\bar{\gamma }\equiv \frac{\lambda (9 \lambda -4)+8 d [\lambda (3 \lambda +4)-6]-16 d^2 (1-\lambda ) (5+\lambda )}{8 (1+2 d)^2}$. This cutoff decreases in d, and increases in $\lambda$ as follows:

$$\begin{aligned} \frac{\partial \bar{\gamma }}{\partial d}= & {} -\frac{(4 d+3) (\lambda -2)^2}{2 (2 d+1)^3}<0,\\ \frac{\partial \bar{\gamma }}{\partial \lambda }= & {} \frac{8 d (2 d (\lambda +2)+3 \lambda +2)+9 \lambda -2}{4 (2 d+1)^2}>0. \end{aligned}$$

1.5 A.5 Proof of Proposition 1

Simultaneously solving for $z_i$ and $z_j$ in the best response function $z_i(z_j)$, and $z_j(z_i)$ yields the equilibrium abatement

$$\begin{aligned} z_i(b_i,b_j)= \frac{1}{B}\left[ a (4 d (4 d+\lambda +2)+3 \lambda -2) \left( 4 d (3+2(\gamma _j- b_j \theta )-\lambda (2 \lambda +3))+4(\gamma _j- b_j \theta )-6 \lambda ^2+\lambda \right) \right] \end{aligned}$$

for each firm i, where the term B is defined as

$$\begin{aligned} B\equiv & {} 3 \lambda ^2 (6 \theta (b_i+b_j)-6 (\gamma _i+\gamma _j)+1)+8 \lambda (-\theta (b_i+b_j)+\gamma _i+\gamma _j)+16 (\gamma _i-b_i \theta ) (\gamma _j-b_j \theta )\\&+32 d^3 \left[ \lambda ^2 (2 \theta (b_i+b_j)-2 (\gamma _i+ \gamma _j+1)-8 \lambda (-\theta (b_i+b_j)+\gamma _i+\gamma _j)+4 b_i \theta b_j \theta -\gamma _j)-10 \theta b_i+b_j)\right. \\&+\left. 2 \gamma _i (2(\gamma _j-b_j \theta )+5)+10 \gamma _j+10 \lambda ^3-36 \lambda +21\right] +16 d^2 \left[ -4 \lambda ^2 (-2 \theta (b_i+b_j)+2 (\gamma _i+\gamma _j)+7)-\right. \\&\left. 16 \lambda (-\theta (b_i+b_j)+\gamma _i+\gamma _j)+2 (6 b_i \theta (b_j\theta -\gamma _j)+\gamma _i (6(\gamma _j-b_j \theta )+11))-22 \theta (b_i+b_j)+22 \gamma _j+2 \lambda ^4\right. \\&\left. +29 \lambda ^3-40 \lambda +27\right] +2 d \left[ 48 \left( -\theta (b_i \gamma _j+b_i+b_j \gamma _i+b_j)+b_i b_j \theta ^2+\gamma _i \gamma _j+\gamma _i+\gamma _j\right) \right. \\&\left. +\lambda ^2 (42 \theta (b_i+b_j)-42 \gamma _i-42 \gamma _j-155)+12 \lambda (2 \theta (b_i+b_j)-2 \gamma _i-2 \gamma _j+3)+24 \lambda ^4+70 \lambda ^3\right] \\&+18 \lambda ^4-21 \lambda ^3. \end{aligned}$$

When the EG is absent, $b_i=b_j=0$, each firm i’s equilibrium abatement is

$$\begin{aligned} z_i(0,0)=\frac{1}{C} \left[ a (4 d (4 d+\lambda +2)+3 \lambda -2) \left( 4 \gamma _j+4 d (2 \gamma _j-\lambda (2 \lambda +3)+3)-6 \lambda ^2+\lambda \right) \right] \end{aligned}$$

where the term C is defined as

$$\begin{aligned} C\equiv & {} -\lambda ^2 (3 (6 \gamma _i+6 \gamma _j-1)+2 d (42\gamma _i+42 \gamma _j+16 d (4 \gamma _i+4 \gamma _j+d (2 \gamma _i+2 \gamma _j-1)+14)+155))\\&+8 \lambda (\gamma _i+\gamma _j-d (6 \gamma _i+6 \gamma _j+16 d (2 \gamma _i+2\gamma _j+d (2 \gamma _i+2 \gamma _j+9)+5)-9))\\&+16 (\gamma _j (2 d+1) (\gamma _i+2 d (2 \gamma _i (d+1)+5 d+3))+d (6 \gamma _i+d (22\gamma _i+(20 \gamma _i+42) d+27)))\\&+2 (4 d+3)^2 \lambda ^4+(4 d+3) (8 d (10 d+7)-7) \lambda ^3 \end{aligned}$$

1.6 A.6 Proof of Proposition 2

The EG’s marginal benefit is

$$\begin{aligned} MB_i\equiv & {} \frac{1}{2}\beta (ER_i)^{-\frac{1}{2}}\left[ \frac{\partial ER_i}{\partial b_i}\right] +\frac{1}{2}\beta (ER_j)^{-\frac{1}{2}}\left[ \frac{\partial ER_j}{\partial b_i} \right] \\= & {} \frac{1}{2}\beta (ER_i)^{-\frac{1}{2}}\left[ \frac{\partial e_i^{NoEG}}{\partial b_i}-\frac{\partial e_i^{EG}}{\partial b_i}\right] +\frac{1}{2}\beta (ER_j)^{-\frac{1}{2}}\left[ \frac{\partial e_j^{NoEG}}{\partial b_i}-\frac{\partial e_j^{EG}}{\partial b_i}\right] \end{aligned}$$

We can simplify this further since $\frac{\partial e_i^{NoEG}}{\partial b_i}=\frac{\partial e_j^{NoEG}}{\partial b_i}=0$ and $\frac{\partial e_i^{EG}}{\partial b_i}=\frac{\partial q}{\partial b_i}-\frac{\partial z_i}{\partial b_i}$, where $q(t(z_i(b_i,b_j),z_j(b_i,b_j)))$. Therefore,

$$\begin{aligned} \frac{\partial q}{\partial b_i}=\frac{\partial q}{\partial t}\frac{\partial t}{\partial z_i}\frac{\partial z_i}{\partial b_i}+\frac{\partial q}{\partial t}\frac{\partial t}{\partial z_i}\frac{\partial z_j}{\partial b_i}, \end{aligned}$$

which simplifies further to $\frac{\partial q}{\partial b_i}=\frac{\partial q}{\partial t}\frac{\partial t}{\partial z_i}\left( \frac{\partial z_i}{\partial b_i}+\frac{\partial z_j}{\partial b_i} \right)$. We also know that since $t(Z)=t(z_i+z_j)$, then $\frac{\partial t}{\partial z_i}=\frac{\partial t}{\partial z_j}$. Substituting this into $MB_i$, we obtain

$$\begin{aligned} MB_i&\equiv \frac{1}{2}\beta (ER_i)^{-\frac{1}{2}}\left[ \frac{\partial z_i}{\partial b_i}-\frac{\partial q}{\partial t}\frac{\partial t}{\partial z_i}\left( \frac{\partial z_i}{\partial b_i}+\frac{\partial z_j}{\partial b_i} \right) \right] +\frac{1}{2}\beta (ER_j)^{-\frac{1}{2}}\left[ \frac{\partial z_j}{\partial b_i}-\frac{\partial q}{\partial t}\frac{\partial t}{\partial z_i}\left( \frac{\partial z_i}{\partial b_i}+\frac{\partial z_j}{\partial b_i} \right) \right] .\\ \end{aligned}$$

1.7 A.7 Robustness Checks

1.7.1 A.7.1Higher $\theta =0.45$

Since $\theta$ only shows up in the EG’s problem, the equilibrium values in the absence of the EG coincide with those in Tables 1b, 15 and 16.

Table 15 Equilibrium collaboration efforts when the EG collaborates with both firms at $\theta =0.45$

Table 16 Equilibrium collaboration efforts and elasticities when the EG collaborates with both firms at $\theta =0.45$

1.7.2 A.7.2 Higher $\beta =0.2$.

Since $\beta$ only affects the EG’s problem, the equilibrium values in the absence of the EG coincide with those in Tables 1b, 17, 18, 19, 20 and 20.

Table 17 Equilibrium collaboration efforts when the EG collaborates with both firms at $\beta =0.2$  

Table 18 Equilibrium collaboration efforts and elasticities when the EG collaborates with both firms at $\beta =0.2$

Table 19 Equilibrium levels when d=1.25.

Table 20 Equilibrium collaboration efforts and elasticities when the EG collaborates with both firms at $d=1.25$

1.7.3 A.7.4 Higher $c_{EG}=0.1$  

Since $c_{EG}$ only affects the EG’s problem, the equilibrium values in the absence of the EG coincide with those in Tables 1b and 21. The equilibrium values in this case are shown in Table 21.

Table 21 Equilibrium collaboration efforts when the EG collaborates with both firms at $c_{EG}=0.1$  

1.7.4 A.7.5 Higher $\lambda =0.2$

Table 22. Table 22 shows the equilibrium values when λ=0.2.e 22.

Table 22 Equilibrium levels when λ=0.2.

1.7.5 A.7.6 Higher $a=2$

Table 23. Table 23 shows the equilibrium values when a=2.e 23.

Table 23 Equilibrium levels when λ=0.2.

1.8 A.8 No EG, Regulation Present

In this case, there is no actor in the first stage and the results from the fourth stage (Lemma 1) and the third stage (Lemma 2) are unchanged:

$$\begin{aligned} q_i= & {} \frac{1}{3} (a-t+2 \lambda z_i-\lambda z_j),\\ t= & {} \frac{2a(4d-1)-(z_i+z_j)[\lambda +4d(3-\lambda )]}{4(1+2d)}. \end{aligned}$$

Second Stage We can use the result from Proposition 1 where $z_i(b_i,b_j)$ is evaluated at $b_i=b_j=0$ to obtain each firm i’s equilibrium investment in abatement in the absence of the EG,

$$\begin{aligned} z_i^{NoEG}=\frac{1}{C} \left[ a (4 d (4 d+\lambda +2)+3 \lambda -2) \left( 4 \gamma _j+4 d (2 \gamma _j-\lambda (2 \lambda +3)+3)-6 \lambda ^2+\lambda \right) \right] . \end{aligned}$$

which entails equilibrium profits of

$$\begin{aligned} \pi _i^{NoEG}=\frac{1}{9} \left[ a^2+2 \lambda (a-t) (2 z_i^{NoEG}-z_j^{NoEG})-2 a t+t^2-\lambda ^2 (2z_i^{NoEG}-z_j^{NoEG})^2\right] + t z_i^{NoEG}. \end{aligned}$$

Social welfare in this case is

$$\begin{aligned} SW=\frac{1}{2}[q_i+q_j]^2+\pi _i+\pi _j+t[q_i+q_j-z_i-z_j]-d[q_i+q_j-z_i-z_j]^2, \end{aligned}$$

where the NoEG superscripts are removed for readability.

1.9 A.9 No Regulation, EG Present

Fourth stage In this case, the fourth stage remains unchanged except now we treat $t=0$, and the results from Lemma 1 become,

$$\begin{aligned} q_i(z_i,z_j)= & {} \frac{1}{3}\left( a+\lambda (2z_i-z_j)\right) ,\\ \pi _i(z_i,z_j)= & {} \left( q_i(z_i,z_j)\right) ^2. \end{aligned}$$

Second Stage In the absence of the regulator, there is no player in the third stage, so we proceed to the second stage of the game where each firm i solves

$$\begin{aligned} \underset{z_i\ge 0}{\max }\,\pi _i(z_i,z_j)-\frac{1}{2}(\gamma _i-\theta b_i)(z_i)^2. \end{aligned}$$

The first-order condition is

$$\begin{aligned} \frac{4}{9} \lambda (a+ \lambda (2z_i-z_j))- (\gamma _i- \theta b_i )z_i=0, \end{aligned}$$

and firm i’s best response function is

$$\begin{aligned} z_i(z_j)=\frac{4a \lambda }{9(\gamma _i- b_i \theta )-8 \lambda ^2}-\frac{4 \lambda ^2 }{9(\gamma _i- b_i \theta )-8 \lambda ^2}z_j. \end{aligned}$$

Firm j has a symmetric best response function. Simultaneously solving for $z_i$ and $z_j$, we find

$$\begin{aligned} z_i^{NoReg}=\frac{4 a \lambda \left( 3 ( \gamma _j-\theta b_j )-4 \lambda ^2\right) }{27 (\gamma _i-\theta b_i ) (\gamma _j- \theta b_j)-24 \lambda ^2 [(\gamma _i- \theta b_i)+(\gamma _j- \theta b_j)]+16 \lambda ^4}. \end{aligned}$$

First stage The EG’s problem remains

$$\begin{aligned} \underset{b_i,b_j\ge 0}{\max }\, \, [\underbrace{\beta (ER_i)^\frac{1}{2}-c_{EG}(b_i)^2}_{\text {Firm}\,\, i}] + [\underbrace{\beta (ER_j)^\frac{1}{2}-c_{EG}(b_j)^2}_{\text {Firm}\,\,j}]. \end{aligned}$$

In the absence of the regulator, the firm’s abatement is not impacted by an emissions fee (as $t=0$) and solely incentivized by how abatement impacts demand, $\lambda$. The EG anticipates this when choosing its collaboration efforts $b_i$ and $b_j$.

Social welfare in this case is

$$\begin{aligned} SW=\frac{1}{2}[q_i+q_j]^2+\pi _i+\pi _j-d[q_i+q_j-z_i-z_j]^2-c_{EG}(b_i^2+b_j^2). \end{aligned}$$

1.10 A.10 No Regulation, no EG

In the absence of both the EG and the regulator, the game only includes stages two and four.

Fourth stage We again use our result from Lemma A1 where $t=0$, which yields

$$\begin{aligned} q_i(z_i,z_j)= & {} \frac{1}{3}\left( a+\lambda (2z_i-z_j)\right) ,\\ \pi _i(z_i,z_j)= & {} \left( q_i(z_i,z_j)\right) ^2. \end{aligned}$$

Second Stage Each firm i’s problem in the second stage is

$$\begin{aligned} \underset{z_i\ge 0}{\max }\,\, \frac{1}{9} (a+ \lambda (2 z_i-z_j))^2-\frac{1}{2}\gamma _i (z_i)^2, \end{aligned}$$

with first-order condition

$$\begin{aligned} \frac{4}{9} \lambda (a+(\lambda z_i- z_j))-\gamma _i z_i=0, \end{aligned}$$

and best response function

$$\begin{aligned} z_i(z_j)=\frac{4 a\lambda }{9 \gamma _i-8 \lambda ^2}-\frac{4\lambda ^2 }{9 \gamma _i-8 \lambda ^2}z_j. \end{aligned}$$

Firm j has a symmetric best response function. Simultaneously solving for $z_i$ and $z_j$, we obtain

$$\begin{aligned} z_i^{NoEG,NoReg}=\frac{4 a \lambda \left( 3 \gamma _j-4 \lambda ^2\right) }{27 \gamma _i \gamma _j-24 \lambda ^2 (\gamma _i+\gamma _j)+16 \lambda ^4}, \end{aligned}$$

which coincides with $z_i^{NoReg}$ when evaluated at $b_i=b_j=0$ (see Appendix 1). Inserting this equilibrium abatement level into firm i’s equilibrium output, we obtain that

$$\begin{aligned} q_i^{NoEG,NoReg}=\frac{3 a \gamma _i \left( 3 \gamma _j-4 \lambda ^2\right) }{27 \gamma _i \gamma _j-24 \lambda ^2 (\gamma _i+\gamma _j)+16 \lambda ^4}, \end{aligned}$$

which entails equilibrium profits of

$$\begin{aligned} \pi _i^{NoEG,NoReg}=\frac{a^2 \gamma _i \left( 9 \gamma _i-8 \lambda ^2\right) \left( 3 \gamma _j-4 \lambda ^2\right) ^2}{\left( 27 \gamma _i \gamma _j-24 \lambda ^2 (\gamma _i+\gamma _j)+16 \lambda ^4\right) ^2}. \end{aligned}$$

Social welfare in this case is

$$\begin{aligned} SW=\frac{1}{2}[q_i+q_j]^2+\pi _i+\pi _j-d[q_i+q_j-z_i-z_j]^2, \end{aligned}$$

which, when evaluated at the equilibrium is

$$\begin{aligned} SW= & {} \frac{1}{\left( 27 \gamma _i \gamma _j-24 \lambda ^2 (\gamma _i+\gamma _j)+16 \lambda ^4\right) ^2}4 a^2 [-6 \lambda ^4 \left( -9 \gamma _i^2-22 \gamma _i \gamma _j-9 \gamma _j^2+2 d (\gamma _i+\gamma _j) (3 \gamma _i+3 \gamma _j-16)\right) \\&-72 d \lambda ^3 \left( \gamma _i^2+6 \gamma _i \gamma _j+\gamma _j^2\right) -81 \gamma _i^2 \gamma _j^2 (d-1)-32 \lambda ^6 (\gamma _i+\gamma _j+8 d)+192 d \lambda ^5 (\gamma _i+\gamma _j)\\&+18 \lambda ^2 (\gamma _i+\gamma _j) (-7 \gamma _i \gamma _j+\gamma _i (6 \gamma _j-2) d-2 \gamma _j d)+108 \gamma _i \gamma _j d \lambda (\gamma _i+\gamma _j)]. \end{aligned}$$

1.11 A.11 Proof of Proposition 3

The EG’s marginal benefit is

$$\begin{aligned} MB_i\equiv & {} \beta \left[ \frac{\partial ER_i}{\partial b_i}\right] +\beta \left[ \frac{\partial ER_j}{\partial b_i} \right] = \beta \left[ \frac{\partial ER_i}{\partial b_i}+\frac{\partial ER_j}{\partial b_i}\right] \\= & {} \beta \left[ \frac{\partial e_i^{NoEG}}{\partial b_i}-\frac{\partial e_i^{EG}}{\partial b_i}+ \frac{\partial e_j^{NoEG}}{\partial b_i}-\frac{\partial e_j^{EG}}{\partial b_i}\right] \end{aligned}$$

We can simplify this further since $\frac{\partial e_i^{NoEG}}{\partial b_i}=\frac{\partial e_j^{NoEG}}{\partial b_i}=0$ and $\frac{\partial e_i^{EG}}{\partial b_i}=\frac{\partial q}{\partial b_i}-\frac{\partial z_i}{\partial b_i}$, where $q(t(z_i(b_i,b_j),z_j(b_i,b_j)))$. Therefore,

$$\begin{aligned} \frac{\partial q}{\partial b_i}=\frac{\partial q}{\partial t}\frac{\partial t}{\partial z_i}\frac{\partial z_i}{\partial b_i}+\frac{\partial q}{\partial t}\frac{\partial t}{\partial z_i}\frac{\partial z_j}{\partial b_i}, \end{aligned}$$

which simplifies further to $\frac{\partial q}{\partial b_i}=\frac{\partial q}{\partial t}\frac{\partial t}{\partial z_i}\left( \frac{\partial z_i}{\partial b_i}+\frac{\partial z_j}{\partial b_i} \right)$. We also know that since $t(Z)=t(z_i+z_j)$, then $\frac{\partial t}{\partial z_i}=\frac{\partial t}{\partial z_j}$. Substituting this into $MB_i$, we obtain

$$\begin{aligned} MB_i\equiv & {} \beta \left[ \frac{\partial z_i}{\partial b_i}-\frac{\partial q}{\partial t}\frac{\partial t}{\partial z_i}\left( \frac{\partial z_i}{\partial b_i}+\frac{\partial z_j}{\partial b_i} \right) +\frac{\partial z_j}{\partial b_i}-\frac{\partial q}{\partial t}\frac{\partial t}{\partial z_i}\left( \frac{\partial z_i}{\partial b_i}+\frac{\partial z_j}{\partial b_i} \right) \right] ,\\= & {} \beta \left[ \frac{\partial z_i +z_j}{\partial b_i}-2\frac{\partial q}{\partial t}\frac{\partial t}{\partial z_i}\left( \frac{\partial z_i+z_j}{\partial b_i} \right) \right] . \end{aligned}$$