Skip to main content
SpringerLink
Log in

Prediction of SAMPL3 host–guest binding affinities: evaluating the accuracy of generalized force-fields

  • Published:
Journal of Computer-Aided Molecular Design Aims and scope Submit manuscript

Abstract

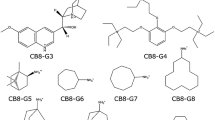
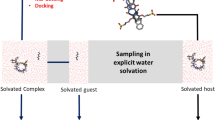
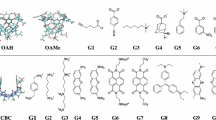
We used the second-generation mining minima method (M2) to compute the binding affinities of the novel host–guest complexes in the SAMPL3 blind prediction challenge. The predictions were in poor agreement with experiment, and we conjectured that much of the error might derive from the force field, CHARMm with Vcharge charges. Repeating the calculations with other generalized force-fields led to no significant improvement, and we observed that the predicted affinities were highly sensitive to the choice of force-field. We therefore embarked on a systematic evaluation of a set of generalized force fields, based upon comparisons with PM6-DH2, a fast yet accurate semi-empirical quantum mechanics method. In particular, we compared gas-phase interaction energies and entropies for the host–guest complexes themselves, as well as for smaller chemical fragments derived from the same molecules. The mean deviations of the force field interaction energies from the quantum results were greater than 3 kcal/mol and 9 kcal/mol, for the fragments and host–guest systems respectively. We further evaluated the accuracy of force-fields for computing the vibrational entropies and found the mean errors to be greater than 4 kcal/mol. Given these errors in energy and entropy, it is not surprising in retrospect that the predicted binding affinities deviated from the experiment by several kcal/mol. These results emphasize the need for improvements in generalized force-fields and also highlight the importance of systematic evaluation of force-field parameters prior to evaluating different free-energy methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Jorgensen WL (2004) The many roles of computation in drug discovery. Science 303:1813–1818

    Article  CAS  Google Scholar 

  2. Gilson MK, Zhou HX (2007) Calculation of protein-ligand binding affinities. Annu Rev Biophys Biomol Struct 36:21–42

    Article  CAS  Google Scholar 

  3. Houk KN, Leach AG, Kim SP, Zhang XY (2003) Binding affinities of host–guest, protein-ligand, and protein-transition-state complexes. Angewandte Chemie Int Edition 42:4872–4897

    Article  CAS  Google Scholar 

  4. Gohlke H, Klebe G (2002) Approaches to the description and prediction of the binding affinity of small-molecule ligands to macromolecular receptors. Angewandte Chemie Int Edition 41:2645–2676

    Google Scholar 

  5. Rodinger T, Pomes R (2005) Enhancing the accuracy, the efficiency and the scope of free energy simulations. Curr Opin Struct Biol 15:164–170

    Article  CAS  Google Scholar 

  6. Rezac J, Fanfrlik J, Salahub D, Hobza P (2009) Semiempirical quantum chemical PM6 method augmented by dispersion and H-bonding correction terms reliably describes various types of noncovalent complexes. J Chem Theory Comput 5:1749–1760

    Article  CAS  Google Scholar 

  7. Chang CE, Gilson MK (2004) Free energy, entropy, and induced fit in host–guest recognition: calculations with the second-generation mining minima algorithm. J Am Chem Soc 126:13156–13164

    Article  CAS  Google Scholar 

  8. Head MS, Given JA, Gilson MK (1997) ‘‘Mining minima’’: direct computation of conformational free energy. J Phys Chem A 101:1609–1618

    Article  CAS  Google Scholar 

  9. Chang CE, Potter MJ, Gilson MK (2003) Calculation of molecular configuration integrals. J Phys Chem B 107:1048–1055

    Article  CAS  Google Scholar 

  10. Gilson MK (1993) Multiple-site titration and molecular modeling—2 rapid methods for computing energies and forces for ionizable groups in proteins. Proteins Struct Funct Genet 15:266–282

    Article  CAS  Google Scholar 

  11. Qiu D, Shenkin PS, Hollinger FP, Still WC (1997) The GB/SA continuum model for solvation. A fast analytical method for the calculation of approximate Born radii. J Phys Chem A 101:3005–3014

    Article  CAS  Google Scholar 

  12. Gilson MK, Honig B (1988) Calculation of the total electrostatic energy of a macromolecular system—solvation energies, binding-energies, and conformational-analysis. Proteins Struct Funct Genet 4:7–18

    Article  CAS  Google Scholar 

  13. Sitkoff D, Sharp KA, Honig B (1994) Accurate calculation of hydration free-energies using macroscopic solvent models. J Phys Chem 98:1978–1988

    Article  CAS  Google Scholar 

  14. Madura JD, Briggs JM, Wade RC, Davis ME, Luty BA, Ilin A, Antosiewicz J, Gilson MK, Bagheri B, Scott LR, Mccammon JA (1995) Electrostatics and diffusion of molecules in solution—simulations with the University-of-Houston Brownian dynamics program. Comput Phys Commun 91:57–95

    Article  CAS  Google Scholar 

  15. Chang CE, Gilson MK (2003) Tork: conformational analysis method for molecules and complexes. J Comput Chem 24:1987–1998

    Article  CAS  Google Scholar 

  16. Chen W, Huang J, Gilson MK (2004) Identification of symmetries in molecules and complexes. J Chem Inf Comput Sci 44:1301–1313

    Article  CAS  Google Scholar 

  17. Momany FA, Rone R (1992) Validation of the general-purpose quanta(R)3.2/Charmm(R) force-field. J Comput Chem 13:888–900

    Article  CAS  Google Scholar 

  18. Gilson MK, Gilson HSR, Potter MJ (2003) Fast assignment of accurate partial atomic charges: an electronegativity equalization method that accounts for alternate resonance forms. J Chem Inf Comput Sci 43:1982–1997

    Article  CAS  Google Scholar 

  19. Trott O, Olson AJ (2010) AutoDock Vina: improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. J Comput Chem 31:455–461

    CAS  Google Scholar 

  20. Mohamadi F, Richards NGJ, Guida WC, Liskamp R, Lipton M, Caufield C, Chang G, Hendrickson T, Still WC (1990) Macromodel—an integrated software system for modeling organic and bioorganic molecules using molecular mechanics. J Comput Chem 11:440–467

    Article  CAS  Google Scholar 

  21. Hess B, Kutzner C, van der Spoel D, Lindahl E (2008) GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation. J Chem Theory Comput 4:435–447

    Article  CAS  Google Scholar 

  22. Stewart JJP (1990) Mopac—a semiempirical molecular-orbital program. J Comput Aided Mol Des 4:1–45

    Article  Google Scholar 

  23. Jorgensen WL, Maxwell DS, TiradoRives J (1996) Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J Am Chem Soc 118:11225–11236

    Article  CAS  Google Scholar 

  24. Kaminski GA, Friesner RA, Tirado-Rives J, Jorgensen WL (2001) Evaluation and reparametrization of the OPLS-AA force field for proteins via comparison with accurate quantum chemical calculations on peptides. J Phys Chem B 105:6474–6487

    Article  CAS  Google Scholar 

  25. Weiner SJ, Kollman PA, Nguyen DT, Case DA (1986) An all atom force-field for simulations of proteins and nucleic-acids. J Comput Chem 7:230–252

    Article  CAS  Google Scholar 

  26. Weiner SJ, Kollman PA, Case DA, Singh UC, Ghio C, Alagona G, Profeta S, Weiner P (1984) A new force-field for molecular mechanical simulation of nucleic-acids and proteins. J Am Chem Soc 106:765–784

    Article  CAS  Google Scholar 

  27. Halgren TA (1996) Merck molecular force field.1. Basis, form, scope, parameterization, and performance of MMFF94. J Comput Chem 17:490–519

    Article  CAS  Google Scholar 

  28. Halgren TA (1999) MMFF VI. MMFF94s option for energy minimization studies. J Comput Chem 20:720–729

    Article  CAS  Google Scholar 

  29. Halgren TA (1999) MMFF VII. Characterization of MMFF94, MMFF94s, and other widely available force fields for conformational energies and for intermolecular-interaction energies and geometries. J Comput Chem 20:730–748

    Article  CAS  Google Scholar 

  30. Allinger NL, Yuh YH, Lii JH (1989) Molecular mechanics—the Mm3 Force-Field for Hydrocarbons.1. J Am Chem Soc 111:8551–8566

    Article  CAS  Google Scholar 

  31. Kolossvary I, Guida WC (1996) Low mode search. An efficient, automated computational method for conformational analysis: application to cyclic and acyclic alkanes and cyclic peptides. J Am Chem Soc 118:5011–5019

    Article  CAS  Google Scholar 

  32. Zhou HX, Gilson MK (2009) Theory of free energy and entropy in noncovalent binding. Chem Rev 109:4092–4107

    Article  CAS  Google Scholar 

  33. Vanommeslaeghe K, Hatcher E, Acharya C, Kundu S, Zhong S, Shim J, Darian E, Guvench O, Lopes P, Vorobyov I, MacKerell AD (2010) CHARMM general force field: a force field for drug-like molecules compatible with the CHARMM All-Atom additive biological force fields. J Comput Chem 31:671–690

    CAS  Google Scholar 

  34. Paton RS, Goodman JM (2009) Hydrogen bonding and pi-stacking: how reliable are force fields? A critical evaluation of force field descriptions of nonbonded interactions. J Chem Inf Model 49:944–955

    Article  CAS  Google Scholar 

  35. Berka K, Laskowski R, Riley KE, Hobza P, Vondrasek J (2009) Representative amino acid side chain interactions in proteins. A comparison of highly accurate correlated ab initio quantum chemical and empirical potential procedures. J Chem Theory Comput 5:982–992

    Article  CAS  Google Scholar 

  36. Moghaddam S, Inoue Y, Gilson MK (2009) Host–guest complexes with protein-ligand-like affinities: computational analysis and design. J Am Chem Soc 131:4012–4021

    Article  CAS  Google Scholar 

  37. Moghaddam S, Yang C, Rekharsky M, Ko YH, Kim K, Inoue Y, Gilson MK (2011) New ultrahigh affinity host–guest complexes of Cucurbit[7]uril with Bicyclo[2.2.2]octane and Adamantane guests: thermodynamic analysis and evaluation of M2 affinity calculations. J Am Chem Soc 133:3570–3581

    Article  CAS  Google Scholar 

  38. Chen W, Chang CE, Gilson MK (2004) Calculation of cyclodextrin binding affinities: energy, entropy, and implications for drug design. Biophys J 87:3035–3049

    Article  CAS  Google Scholar 

  39. Merz KM (2010) Limits of free energy computation for protein-ligand interactions. J Chem Theory Comput 6:1769–1776

    Article  CAS  Google Scholar 

  40. Faver JC, Benson ML, He X, Roberts BP, Wang B, Marshall MS, Sherrill CD, Merz KM (2011) The energy computation paradox and ab initio protein folding. Plos One 6:e18868

    Google Scholar 

  41. Wang JM, Wolf RM, Caldwell JW, Kollman PA, Case DA (2004) Development and testing of a general amber force field. J Comput Chem 25:1157–1174

    Article  CAS  Google Scholar 

Download references

Acknowledgments

This publication was made possible by grant no.GM061300 from NIH. Its contents are solely the responsibility of the authors and do not necessarily represent the official views of the NIH.

Author information

Authors and Affiliations

  1. Skaggs School of Pharmacy and Pharmaceutical Sciences, University of California San Diego, 9500 Gilman Drive, Room# 3224, La Jolla, CA, 92093-0736, USA

    Hari S. Muddana & Michael K. Gilson

Authors
  1. Hari S. Muddana
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Michael K. Gilson
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Michael K. Gilson.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Muddana, H.S., Gilson, M.K. Prediction of SAMPL3 host–guest binding affinities: evaluating the accuracy of generalized force-fields. J Comput Aided Mol Des 26, 517–525 (2012). https://doi.org/10.1007/s10822-012-9544-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10822-012-9544-3

Keywords

Search

Navigation