1 Introduction

Let (W,S) denote a Coxeter system with set of reflections T:={wsw −1:s∈S,w∈W}. The Bruhat graph of (W,S) is the directed graph B(W):=(V,E) with V=W and (u,v)∈E for u,v∈W if ℓ(u)<ℓ(v) and there exists t∈T such that ut=v. Here, ℓ(⋅) denotes the length function of (W,S). Furthermore, if u,v∈W, we denote the set of u–v paths of length (number of edges) k by B k (u,v), and let B(u,v):=⋃ k B k (u,v). As a convention, we will denote Δ∈B k (u,v) in one of two ways:

  1. (i)

    Δ=(x 0=u<x 1<⋯<x k =v), with x i ∈W, when we wish to refer to the vertices of Δ, and

  2. (ii)

    Δ=(t 1,t 2,…,t k ), with t i ∈T and x i−1 t i =x i , with i=1,…,k, when we wish to refer to the edges that Δ traverses.

One can define a partial order ≤, called the Bruhat order, as follows: u≤v if there exists a directed u–v path in B(W). Bruhat intervals are endowed with many combinatorial properties; for example, they are Eulerian posets, that is, they are graded posets in which every nontrivial interval has the same number of elements of even rank as of odd rank.

A reflection order < T is a total order on T such that, for any Coxeter system of the form (〈t 1,t 2〉,{t 1,t 2}) with t 1,t 2∈T, either

Reflection orders have been shown to exist and have proven to be an important tool in the study of Coxeter groups (see, e.g., [11], [4, Chap. 5]). An initial section A T of a reflection order < T is a subset of T satisfying a< T b for all a∈A T and b∈T∖A T .

For w∈W, we define the negative set of w, denoted by N(w), to be the set of reflections that shorten the length of w, i.e., N(w):={t∈T∣ℓ(wt)<ℓ(w)}. Notice that if s 1⋯s k is a reduced expression for w, then N(w)={t 1,…,t k }, where t i =s k ⋯s k−i+2 s k−i+1 s k−i+2⋯s k for i=1,…,k. Furthermore, the total order defined by

$$t_{k}<_w t_{k-1}<_w\cdots <_w t_{1} $$

is said to be induced by the reduced expression s 1⋯s k for w. Dyer showed that finite initial sections are induced by reduced expressions.

Lemma 1

([11], Lemma 2.11)

A T is a finite initial section of a reflection order if and only if A T =N(w) for some w∈W. In other words A T is a finite initial section of a reflection order if and only if it is induced by a reduced expression for some w∈W.

Notice that [4, Proposition 2.3.1(i)] gives the existence of a unique longest-length element w 0 for finite W, that is, w 0≥w for all w∈W. Moreover, |N(w 0)|=ℓ(w 0)=|T| by [4, Proposition 2.3.2(iv)], and so we have the following corollary.

Corollary 1

If W is finite, then all reflection orders on T are induced by a choice of reduced expression for w 0.

Definition 1

(i) The poset P is said to be EL-labelable (Edge-wise Lexicographically labelable) if there exists an edge labeling λ of P so that every subinterval [x,y]∈P has a unique maximal chain that is rising. Furthermore, such a chain is lexicographically earlier than any other maximal chain of [x,y].

(ii) The λ above is called an EL-labeling of P.

In [12] and [11], Dyer proved two important consequences that follow from the existence of reflection orders. One such consequence is the following theorem.

Theorem 1

([11], Proposition 4.3)

Let [u,v] be a Bruhat interval. Then [u,v] is EL-labelable.

The second consequence is an alternative, non-recursive definition of the so-called \(\widetilde{R}\)-polynomials, which is discussed in Sect. 4.

Given a reflection order < T and a path Δ=(t 1,t 2,…,t k )∈B k (u,v), the descent set \(D_{<_{T}}(\varDelta )\) of Δ under < T is defined as \(D_{<_{T}}(\varDelta ):=\{i\in[k-1]:t_{i+1}<_{T}t_{i}\}\). A path Δ is said to be < T -rising, or simply rising, if \(D_{<_{T}}(\varDelta )=\emptyset\). While the descent set of a path depends on the choice of reflection order, the number of rising paths is the same (cf. [4, Proposition 5.3.4]). That is,

Proposition 1

Let u,v∈W, with u≤v, and let < T , \(<'_{T}\) be two reflection orders. Then

$$\bigl|\bigl\{\varGamma\in B(u,v):D_{<_T}(\varGamma)=\emptyset\bigr\}\bigr|= \bigl|\bigl\{ \varGamma\in B(u,v):D_{<_{T}'}(\varGamma)=\emptyset\bigr\}\bigr|. $$

Furthermore there exists at least one rising path in B k (u,v) whenever B k (u,v)≠∅.

Proposition 2

([6], Proposition 3.9)

Let Δ be the lexicographically first path in B k (u,v)≠∅ under a reflection order < T . Then \(D_{<_{T}}(\varDelta )=\emptyset\), i.e., Δ is < T -rising.

Moreover, since the reverse of a reflection order is also a reflection order, it follows that

$$ \bigl |\bigl\{\varGamma\in B_{k}(u,v):D_{<_{T}}( \varGamma)=\emptyset\bigr\}\bigr|=\bigl|\bigl\{\varGamma\in B_{k}(u,v):D_{<_{T}}( \varGamma)=[k-1]\bigr\}\bigr|. $$
(1)

The remainder of the paper is organized as follows: In Sect. 2 we define the shortest path poset for Bruhat intervals. In Sect. 3 we recast the main result of [5] stating that SP(W):=SP(e,w 0) is the union of Boolean algebras, where W is a finite, irreducible Coxeter group and w 0 is its element of longest length, and prove that it admits a symmetric chain decomposition. In Sect. 4 we prove that SP(u,v) is EL-labelable, in fact Gorenstein∗, if there is a unique rising chain under a reflection order. In Sect. 4.2 we derive the nonnegativity of certain coefficients of the complete cd-index. Some of our results have appeared, without proof, in a FPSAC extended abstract in [7].

2 Definition of the shortest path poset

We first need to have a notion of “distance” in B(u,v).

Definition 2

(i) Let Δ be a path of B(u,v) and w be a vertex of Δ. The distance of w on Δ, denoted by d Δ (u,w), is the number of edges in the u–w path of Δ.

(ii) The shortest distance of [u,v], denoted by ℓ s (u,v), is the length of the shortest path of B(u,v). That is, ℓ s (u,v):=min{ℓ:B ℓ (u,v)≠∅}. When the interval is clear from the context, we simply write ℓ s .

Lemma 2

Consider two paths \(\varGamma,\varGamma'\in B_{\ell_{s}}(u,v)\) and let x∈[u,v] be a vertex in both paths. Then d Γ (u,x)=d Γ′(u,x).

Proof

Let \(\varGamma=(x_{0}=u< x_{1}< x_{2}<\cdots< x_{\ell_{s}}=v)\) and \(\varGamma'=(x'_{0}=u< x'_{1}< x'_{2}<\cdots< x'_{\ell_{s}}=v)\). Since x is a vertex of both Γ and Γ′, then x i =x and \(x'_{j}=x\) for some 0≤i,j≤ℓ s .

Notice that d Γ (u,x)=i and d Γ′(u,x)=j. If the two distances are not equal, then one of them is bigger. Suppose without loss of generality that i<j. Then \((x_{i}<x'_{j+1})\) is an edge in the Bruhat graph, and the path \((x_{0}=u<\cdots< x_{i}=x< x'_{j+1}< x'_{j+2}< x'_{\ell_{s}}=v)\) has length i+(ℓ s −j)<ℓ s . This contradicts the definition of ℓ s . Thus i=j. □

Proposition 3

By ignoring the directions of the edges, \(B_{\ell_{s}}(u,v)\) is the Hasse diagram of a graded poset.

Proof

Since B(u,v) is a directed, acyclic graph, the edges of paths in \(B_{\ell_{s}}(u,v)\) give a partial order ≤ s on the elements of [u,v] that are in a u–v path of length ℓ s . This partial order is defined by x≤ s y if and only if x=y or if there is a path (x=y 0<y 1<⋯<y p =y)∈B(x,y) such that each edge (y i−1<y i ) is in a shortest u–v path, for 0<i≤p.

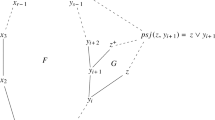
Let (x≤ s y) be an edge in \(B_{\ell_{s}}(u,v)\). Now, to prove the proposition we need to show that x⋖ s y. It suffices to show that there is no path (x 0=x<x 1<x 2<⋯<x k =y) with k>1 such that each edge (x i−1<x i ) is in some path \(\varGamma_{i}\in B_{\ell_{s}}(u,v)\) for 1≤i≤k<ℓ s (refer to Fig. 1).

Fig. 1
figure 1

Illustrating the proof of Proposition 3. Path Γ i goes through edge (x i−1<x i ) for 1≤i≤k

Full size image

Notice that if such a path existed, then \(B_{\ell_{s}}(u,v)\) (when ignoring directions) would not be a Hasse diagram, as there would be edges that would not represent cover relations. So let us assume for the sake of contradiction that such a path exists. Then

$$ d_{\varGamma}(u,x)=d_{\varGamma_k}(u,x_{k-1}), $$
(2)

for otherwise one of them, say d Γ (u,x), is bigger than the other one. Thus there exists a u–v path Γ′ formed by the edges of Γ k up to y and then continue on the edges of Γ. Notice that the length of Γ′ is \(d_{\varGamma_{k}}(u,y)+(\ell_{s}-d_{\varGamma}(u,y))<\ell_{s}\). This contradicts the definition of ℓ s , and thus \(d_{\varGamma}(u,x)=d_{\varGamma_{k}}(u,x_{k-1})\). Similarly, we obtain

Hence \(d_{\varGamma}(u,x)=d_{\varGamma_{1}}(u,x_{1})=d_{\varGamma_{2}}(u,x_{2})-1=\cdots=d_{\varGamma_{k}}(u,x_{k-1})-(k-1)\). However, since k>1 this contradicts (2). Thus the edges of \(B_{\ell_{s}}(u,v)\) are the cover relations of a poset. Moreover, notice that this poset is graded by r(x):=d Γ (u,x) where \(\varGamma\in B_{\ell_{s}}(u,v)\) contains the vertex x. This is a well-defined rank function by Lemma 2.

Finally, notice that if (x<y) is an edge in \(B_{\ell_{s}}(u,v)\) then there does not exist an x–y path containing an element other than x and y. Thus x⋖y by definition. □

We call the poset in Proposition 3 the shortest path poset of u,v, which we denote by SP(u,v). We consider the edges of SP(u,v) to be labeled by the corresponding edges in \(B_{\ell_{s}}(u,v)\).

3 SP(W), for finite, irreducible Coxeter groups

Let W be a finite, irreducible Coxeter group. We let SP(W):=SP(e,w 0). Figure 2 depicts B 2 and SP(B 2), respectively. The rank of SP(B 2) is two since that is the length of the shortest paths in B(B 2).

Fig. 2
figure 2

B(B 2) and SP(B 2)

Full size image

For any w∈W, one can write t 1 t 2⋯t n =w for some t 1,t 2,…,t n ∈T. If n is minimal, then we say that w is T-reduced, and that the absolute length of w is n. The absolute length of w is denoted by ℓ T (w).

Notice that for w∈W, if ℓ T (w)=ℓ, then t 1 t 2⋯t ℓ =w for some reflections t 1,t 2,…,t ℓ in T, but this does not mean that (t 1,t 2,…,t ℓ ) is a (directed) path in B(e,w). Nevertheless, it is shown in [5] that for finite W and w=w 0, (t 1,t 2,…,t ℓ ), and any of its permutations (t τ(1),t τ(2),…,t τ(ℓ)), τ∈S ℓ , is a path in B(W). To be more specific, one has the following theorem.

Theorem 2

(Theorem 1.1, [5])

Let W be a finite Coxeter group and ℓ 0=ℓ T (w 0), the absolute length of the longest element of W. Then SP(W) is isomorphic to the union of Boolean posets of rank ℓ 0.

We point out that the union of the Boolean posets could share more elements than e and w 0. For instance, consider SP(B 3) depicted in Fig. 3. In addition to 123 and 1  2  3, there are other elements shared by more than one boolean copy; for instance, 123 and 123. Nonetheless each maximal chain belongs to a unique boolean copy.

Fig. 3
figure 3

SP(B 3) has four copies of \(\mathcal{B}_{3}\). Notice that while these copies intersect, each maximal chain is in a unique Boolean poset

Full size image

3.1 Symmetric chain decomposition

A graded poset P of rank n admits a symmetric chain decomposition if it can be partitioned into saturated chains C 1,C 2,…,C ℓ that are centrally symmetric, that is, the rank of the minimum element equals the corank of the maximum element for each C i . Furthermore, P is said to admit a symmetric boolean decomposition if it can be partitioned into pieces P 1,P 2,…,P k where each P i is isomorphic to \(\mathcal {B}_{n-2k_{i}}\), the Boolean algebra of rank n−2k i , with k i being the rank of the minimum element of P i . Examples of posets that exhibit symmetric boolean decompositions are the noncrossing partitions of type A and B (see [17] and [9]).

The following remark is in order (see, e.g., [15]):

Remark 1

If a poset P admits a symmetric boolean decomposition, then P admits a symmetric chain decomposition.

Let \(\mathcal{P}=\{P_{1},P_{2},\ldots, P_{k}\}\) be family of graded posets of rank n that do not share any elements. Furthermore, denote the minimum and maximum elements of each P i by \(\widehat{0}_{i}\), \(\widehat{1}_{i}\), respectively, and let \(S(\mathcal{P})\) denote the poset

$$S(\mathcal{P}):=\coprod_{i=1}^{k} (\widehat{0}_{i}, \widehat{1}_{i})\cup\{\widehat{0},\widehat{1}\}, $$

where \(\widehat{0}\) and \(\widehat{1}\) are defined to be the minimum and maximal element of \(\coprod_{i=1}^{k} (\widehat{0}_{i},\widehat{1}_{i})\), respectively. Here, \((\widehat{0}_{i},\widehat{1}_{i})\) denotes the poset P i with its minimum and maximum elements removed. Now we have the following lemma:

Lemma 3

If P i , 1≤i≤k, admits a symmetric boolean decomposition, then \(S(\mathcal{P})\) admits a symmetric chain decomposition.

Proof

Let C 1,…,C q be a symmetric chain decomposition of P 1 and let us assume, without loss of generality, that C 1 contains \(\widehat{1}_{1}\) and \(\widehat{0}_{1}\). Then C,C 2,…,C q is a symmetric chain decomposition of \((\widehat{0}_{1},\widehat{1}_{1})\), where \(C=C_{1}\setminus\{\widehat{0}_{1},\widehat{0}_{1}\}\). By Remark 1, each \((\widehat{0}_{j},\widehat{1}_{j})\), 2≤j≤k, has a symmetric chain decomposition. Therefore there exists a symmetric chain decomposition D 1,D 2,…,D r for

$$\coprod_{j=2}^{k}(\widehat{0}_{j}, \widehat{1}_{j}). $$

Hence \(C\cup\{\widehat{0},\widehat{1}\}, C_{2},\ldots, C_{q}, D_{1},\ldots, D_{r}\) is a symmetric chain decomposition of \(S(\mathcal{P})\). □

We are now ready to prove the following proposition.

Proposition 4

SP(W) exhibits a symmetric chain decomposition.

Proof

By Theorem 2, SP(W) is the union of boolean posets. Thus one can remove cover relations from SP(W) to obtain a family of posets \(\mathcal{P}=\{P_{1},\ldots,P_{k}\}\), each one of them being isomorphic to a Boolean algebra of rank ℓ T (w 0), so that \(\mathit{SP}(W)=S(\mathcal{P})\) as sets. Lemma 3 yields the result that \(S(\mathcal{P})\) has a symmetric chain decomposition, and therefore so does SP(W). □

One question that arises from the previous proposition is the following: What Bruhat intervals exhibit a symmetric boolean/chain decomposition? Billey [3] provides a sufficient condition for the existence of a symmetric chain decomposition for intervals of the form [e,w], where w is an element of A n or B n .

4 Unique rising shortest path

In this section we will show that if there is a unique rising path in \(B_{\ell_{s}}(u,v)\) then SP(u,v) is a Gorenstein∗ poset. As a consequence, we derive nonnegativity of certain coefficients of \(\widetilde {\psi }_{u,v}(\textbf {c},\textbf {d})\). We start with some topological definitions.

A simplicial complex Δ is said to be Cohen–Macaulay over \(\mathbb {K}\) (\(\mathbb {K}\) a field or ℤ) if the reduced homology

$$\widetilde{H}_{i}(\mbox {link}_{\varDelta } F;\mathbb {K}) = 0\quad\text{for all}\ F \in \varDelta \ \text{and}\ i < \dim \mbox {link}_{\varDelta }F. $$

Here, link Δ F:={G∈Δ:G∪F∈Δ and G∩F=∅}. A poset is said to be Cohen–Macaulay if its order complex is Cohen–Macaulay. A poset is said to be Gorenstein ∗ if it is Eulerian and Cohen–Macaulay (cf. [14, Sect. 2.1]).

It turns out that if a poset is EL-labelable, then it is Cohen–Macaulay for all \(\mathbb {K}\) [19, Theorem 4.1.9]. So to show that a poset is Gorenstein*, it is enough to show that it is EL-labelable and Eulerian. This is the case for SP(u,v) if there is a unique rising chain.

4.1 \(\widetilde{R}\)-polynomials

In the study of Coxeter groups, it is common to encounter the \(\widetilde{R}\)-polynomials, which are defined in the proposition below.

Proposition 5

([4], Proposition 5.3.2)

Let u,v∈W with u≤v and ℓ(vs)<ℓ(v). Then there exists a monic polynomial \(\widetilde{R}(\alpha)\) of degree ℓ(v)−ℓ(u) given by

$$ \widetilde{R}_{u,v}(\alpha)= \begin{cases} \widetilde{R}_{us,vs}(\alpha)&\text{\textit{if}}\ \ell(us)<\ell(u),\ \text{\textit{and}}\\[2pt] \widetilde{R}_{us,vs}(\alpha)+\alpha\widetilde{R}_{u,vs}(\alpha)&\text{\textit{otherwise}.} \end{cases} $$

The \(\widetilde{R}\)-polynomials are used, among other things, to define the R-polynomials, and these are used to define the Kazhdan–Lusztig polynomials from representation theory (see [4]). That is one of the reasons why the \(\widetilde{R}\)-polynomials are of interest.

Dyer used reflection orders to provide a non-recursive definition of the \(\widetilde{R}\)-polynomials.

Theorem 3

([12], Theorem 2.3)

If u≤v, then

$$\widetilde{R}_{u,v}(\alpha)=\sum_{\substack{{\varDelta \in B(u,v)}\\ {D(\varDelta )}=\emptyset}} \alpha^{\ell(\varDelta )}. $$

Dyer’s theorem states that the \(\widetilde{R}_{u,v}(\alpha)\) is simply the generating function of the rising paths in B(u,v). Using this interpretation, we are able to derive the following inequality.

Theorem 4

If u≤x≤v, then \(\widetilde{R}_{u,x}(\alpha)\widetilde{R}_{x,v}(\alpha)\leq \widetilde{R}_{u,v}(\alpha)\) (coefficientwise).

Proof

The inequality is equivalent to saying that there are more rising paths in B(u,v) than rising paths in B(u,x) times the number of rising paths of B(x,v). So it is enough to find an injection

where \(\mathcal{R}(y,z)=\{\varGamma\in B(y,z):D(\varGamma)=\emptyset\}\).

Consider a reflection order < x with initial section N(x). Let (t 1,…,t p ) be a < x -rising path of B(u,x) and let (r 1,…,r q ) be a < x -rising path of B(x,v). Since t p ∈N(x) and \(r_{1}\not\in N(x)\), it follows that t p < x r 1. Hence the path (t 1,…,t p ,r 1,…r q ) is a < x -rising path of B(u,v). By Proposition 1, the number of rising paths is the same under any reflection order. Hence the desired injection φ x is given by concatenating a < x -rising path in B(u,x) and a < x -rising path in B(x,v). □

We no longer need a specific reflection order, and thus from now on we fix a reflection order < T .

Theorem 4 generalizes the following results due to Brenti. All the inequalities are coefficientwise.

Corollary 2

  1. 1.

    [10, Theorem 5.4] If u≤x≤v, then

    $$\alpha^{\ell(v)-\ell(x)}\widetilde{R}_{u,x}(\alpha)\leq\widetilde{R}_{u,v}( \alpha). $$
  2. 2.

    [10, Corollary 5.5] If W is finite and u≤x≤y≤v, then

    $$\alpha^{\ell(v)-\ell(y)+\ell(x)-\ell(u)}\widetilde{R}_{x,y}(\alpha)\leq \widetilde{R}_{u,v}(\alpha). $$
  3. 3.

    [10, Theorem 5.6] Let x,y,z∈W be such that y≤z in Bruhat order and x≤y in weak Bruhat order (this is a coarsening of the Bruhat order). Then

    $$\alpha^{\ell(y)-\ell(x)}\widetilde{R}_{y,z}(\alpha)\leq \widetilde{R}_{x,z}(\alpha). $$

All these inequalities are special cases of Theorem 4. For instance, the first inequality follows immediately from

$$\widetilde{R}_{u,x}(\alpha)\widetilde{R}_{x,v}(\alpha)\leq \widetilde{R}_{u,v}(\alpha)\quad \text{and}\quad \alpha^{\ell(v)-\ell(x)}\leq \widetilde{R}_{x,v}(\alpha). $$

The second inequality follows from

$$\begin{aligned} &\widetilde{R}_{u,x}(\alpha)\widetilde{R}_{x,y}(\alpha) \widetilde{R}_{y,v}(\alpha)\leq\widetilde{R}_{u,v}(\alpha) , \\ & \alpha^{\ell(v)-\ell(y)}\leq \widetilde{R}_{y,v}(\alpha) ,\quad \mathrm{and} \quad \alpha^{\ell(x)-\ell(u)}\leq \widetilde{R}_{u,x}(\alpha). \end{aligned} $$

Finally, the last inequality follows from

$$\widetilde{R}_{x,y}(\alpha)\widetilde{R}_{y,z}(\alpha)\leq \widetilde{R}_{x,z}(\alpha)\quad \text{and}\quad \alpha^{\ell(y)-\ell(x)}\leq \widetilde{R}_{x,y}(\alpha). $$

Of special interest for our purposes is the following inequality.

Proposition 6

If u≤x≤y≤v then \(|\mathcal{R}(x,y)|\leq |\mathcal{R}(u,v)|\).

Proof

Since the interval [u,v] is graded, it is enough to show that the result holds when u⋖x≤y or u≤y⋖v. Either of these cases follow from Theorem 4 since then \(\widetilde{R}_{u,x}(\alpha )=1\) or \(\widetilde{R}_{y,v}(\alpha )=1\), respectively. □

This proposition is a very important ingredient in the proof of the main result of this paper, which now follows.

Theorem 5

Suppose that SP(u,v) has a unique maximal, rising chain. Then SP(u,v) is a Gorenstein ∗ poset.

Proof

We verify that SP(u,v) is EL-labelable (cf. Definition 1(i)). Proposition 2 gives the result that any subinterval of SP(u,v) has at least one rising chain: the lexicographically first one. Moreover, Proposition 6 states that the number of rising chains in any subinterval of SP(u,v) can be at most one. Thus any subinterval of SP(u,v) has a unique rising path that is lexicographically first, and so SP(u,v) is EL-labelable.

We just showed that SP(u,v) is Cohen–Macaulay, as it is EL-labelable, and need only show that SP(u,v) is Eulerian. Notice that any interval of rank 2 of SP(u,v) has two atoms, for otherwise there must be more than one rising chain in some interval (of rank 2) by (1). Thus SP(u,v) is thin (as are Bruhat intervals; see e.g., [4, Lemma 2.7.3] and [4, Theorem 2.7.7]). Therefore the poset P=SP(u,v)∖{u,v} is pure and thin. Hence by [19, Theorem 3.1.12], SP(u,v) is the face poset of a regular CW-decomposition of an (ℓ s −2)-sphere that is homeomorphic to Δ(P), the order complex of P. In particular SP(u,v) must be Eulerian. Hence, SP(u,v) is a Gorenstein∗ poset. □

We finish this section with the following two conjectures.

Conjecture 1

If SP(u,v) has a unique rising chain, then SP(u,v) is a lattice.

This conjecture is inspired by an unpublished result due to Dyer [13] stating that if all paths of the Bruhat graph of [u,v] have length ℓ(v)−ℓ(u), then [u,v] is a lattice (in fact, he showed that [u,v] is isomorphic to the face poset of a polytope).

Furthermore, we believe a stronger conjecture is true.

Conjecture 2

If SP(u,v) has a unique rising chain, then SP(u,v) is isomorphic to a Bruhat interval.

We point out that intervals [u,v] for which their shortest path poset SP(u,v) has a unique rising chain appear frequently. For example, there are 37,467 intervals in S 6 having a unique rising chain, with SP(u,v)≠[u,v] (so the rank of [u,v] is at least three and the rank of SP(u,v) is at least one). For this computer search, we used Stembridge’s Maple package [18].

4.2 Nonnegativity consequences for the complete cd-index

Billera and Brenti’s complete cd -index \(\widetilde{\psi}_{u,v}(\textbf {c},\textbf {d})\) encodes the distribution of the descent sets of [u,v]. The complete cd-index is a non-homogeneous polynomial whose terms have degree one less than the lengths of the paths of B(u,v). The terms of highest degree of \(\widetilde{\psi}_{u,v}(\textbf {c},\textbf {d})\) correspond to the cd-index of the Eulerian poset [u,v], which encodes the flag h-vector of [u,v]. For details, the reader is referred to [2], [1, Sect. 4]. The complete cd-index provides a combinatorial definition of the Kazhdan–Lusztig polynomials, and its study might shed some light on open problems regarding the coefficients of these polynomials.

It has been conjectured that the coefficients of \(\widetilde{\psi}_{u,v}(\textbf {c},\textbf {d})\) are nonnegative [2, Conjecture 6.1]. There is a stronger conjecture for lower intervals, namely \(\widetilde{\psi}_{e,v}(1,1)\leq\varPhi_{\mathcal {B}_{\ell(v)}}(1,1)\), where \(\varPhi_{\mathcal {B}_{\ell(v)}}\) denotes the cd-index of [e,v] as an Eulerian poset (see [1, Conjecture 3]). Our results allow us to conclude that certain terms of \(\widetilde{\psi}_{u,v}(\textbf {c},\textbf {d})\) are nonnegative. If \([\textbf {c}^{\ell_{s}-1}]\widetilde{\psi}_{u,v}(\textbf {c},\textbf {d})\) denotes the coefficient of \(\textbf {c}^{\ell_{s}-1}\), where ℓ s is the shortest distance of [u,v], then we have:

Proposition 7

If \([\textbf {c}^{\ell_{s}-1}]\widetilde{\psi}_{u,v}(\textbf {c},\textbf {d})=1\), the terms of degree ℓ s −1 in \(\widetilde{\psi}_{u,v}(\textbf {c},\textbf {d})\) are nonnegative.

Proof

If \([\textbf {c}^{\ell_{s}-1}]\widetilde{\psi}_{u,v}(\textbf {c},\textbf {d})=1\), Theorem 5 shows that SP(u,v) is Gorenstein*. Therefore, the terms of degree ℓ s −1 in \(\widetilde{\psi}_{u,v}(\textbf {c},\textbf {d})\) coincide with the cd-index of SP(u,v) as an Eulerian poset. Furthermore, the cd-index of Gorenstein∗ posets is nonnegative (see [16]) and therefore the terms of \(\widetilde{\psi}_{u,v}(\textbf {c},\textbf {d})\) of degree ℓ s −1 are also nonnegative. □

In [5], we obtain a stronger result for finite, irreducible Coxeter groups. Namely, we are able to compute the lowest-degree terms of \(\psi_{u,w_{0}}(\textbf {c},\textbf {d})\) in terms of the cd-index of Boolean algebras.

5 Further directions

In general, SP(u,v) will have more than one rising chain. We would like to find a procedure that would allow us to partition SP(u,v) into pieces P 1,…,P k , each one of which has a unique rising chain. A possible approach would be to “flip” the descents of a chain of SP(u,v) into ascents (see [2, Sect. 6]). If each piece P i satisfies enough properties, we hope to conclude that the terms of lowest degree of \(\widetilde{\psi}_{u,v}(\textbf {c},\textbf {d})\) are the sum of nonnegative terms contributed by each P i . There is evidence, both computational and theoretical, supporting this approach (see [8, Chap. 4]).