Skip to main content
SpringerLink
Log in

Mathematical modeling of AC electroosmosis in microfluidic and nanofluidic chips using equilibrium and non-equilibrium approaches

  • Original Paper
  • Published:
Journal of Applied Electrochemistry Aims and scope Submit manuscript

Abstract

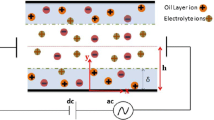
AC electroosmotic micropumps are suggested to be powerful tools for electrolyte dosing in various micro- and nanofluidic systems. In this paper, we compare two modeling approaches for studying the AC electroosmosis in the following micro and nanochannel systems: (i) a traveling-wave AC pump with a spatially continuous wave of electric potential applied on a planar boundary, (ii) a traveling-wave AC pump with a wave of electric potential applied on a set of discrete planar electrodes, and (iii) an AC pump with a set of non-planar electrodes. The equilibrium approach is based on the use of capacitor–resistor boundary conditions for electric potential and the slip boundary conditions for velocity at electrode surfaces. The non-equilibrium approach uses the mathematical model based on the Poisson equation and the non-slip boundary conditions. We have observed discrepancies between the predictions given by the both models and then we have identified their possible reasons. The comparison of the equilibrium and non-equilibrium results further showed three important actualities: (a) how the equilibrium model overestimates or underestimates the net velocity, (b) how the velocity maxima in the frequency characteristics can be shifted, if the equilibrium model assumptions are not satisfied, (c) the parametric region where the equilibrium model is applicable. Because the data are obtained in a dimensionless form, they can be exploited for AC electroosmotic studies. We discuss the limitations of the equilibrium and non-equilibrium models and compare selected predictions with available experimental data.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Abbreviations

A :

Amplitude (V)

c :

Concentration (mol m−3)

C D :

Capacitance of EDL (F m−2)   \(C_{D} = \varepsilon/\lambda_{D}\)

D :

Diffusivity (2 × 10−9 m2 s−1)

f :

Frequency (s−1)

F :

The Faraday constant (96,485 C mol−1)

g :

Gap width (m)   g = x Lm+1 −x R m

h :

Electrode height (m)

H :

Height of a periodic segment (m)

J :

Ion flux intensity (mol m−2s−1)

k :

Wave number (m−1)   k = 2π/L

L :

Length of a periodic segment (m)

L e :

Electrode width (m)   L e = x R m  − x L m

n :

Number of electrodes

n Fx :

Number of finite elements in the x-direction

n Fy :

Number of finite elements in the y-direction

n :

Normal unit vector

p :

Pressure (Pa)

q :

Electric charge density (C m−3)

R :

Molar gas constant (8.314 J K−1mol−1)

t :

Time (s)

t :

Tangential unit vector

T :

Temperature (298.15 K)

T t :

Period of the electric signal (s)   T t  = f −1

v :

Horizontal component of velocity (m s−1)

〈v 〉:

Net velocity (m s−1)

v :

Velocity (m s−1)

w :

Electric potential wave velocity (m s−1)   w = L/T t  = ω/k

x :

Spatial coordinate (m)

y :

Spatial coordinate (m)

α:

Phase of an AC signal

\(\varepsilon\) :

Electrolyte permitivity (6.9503 × 10−10 F m−1)

φ:

Electric potential (V)

η:

Dynamic viscosity (0.001 Pa s)

λ D :

The Debye length (m)   \(\lambda_{D}^{2}=\frac{\varepsilon D}{\sigma}\)

ψ:

Complex electric potential (V)

ρ:

Density (1,000 kg m−3)

σ:

Specific conductivity (S m−1)   \({\sigma}=2 c_{\circ} D \frac{F^{2}}{RT}\)

ω:

Angular frequency (s−1)   ω = 2 πf

Ra:

The Rayleigh number   \(\hbox{Ra} = \frac{\varepsilon}{\eta D}\left(\frac{RT}{F}\right)^{2}= 0.2294\)

Sc:

The Schmidt number   \(\hbox{Sc} =\frac{\eta}{\rho D} =500\)

\({\tilde{\lambda}}_{D}\) :

EDL simplex   \({\tilde{\lambda}}_{D} =\lambda_{D}/L\)

*:

Complex conjugate

∼:

Dimensionless

∧:

Time averaged

+:

Cation

−:

Anion

±:

Either + or −

e :

Electrode

L :

Left boundary of the electrode

R :

Right boundary of the electrode

C :

Center of the electrode

o:

Characteristic value

m :

Index of electrode

slip:

At the slip plane

References

  1. Ramos A, Morgan H, Green NG et al (1998) J Phys D 31:2338

    Article  CAS  Google Scholar 

  2. Ajdari A (2000) Phys Rev E 61:R45

    Article  CAS  Google Scholar 

  3. Campisi M, Accoto D, Dario P (2005) J Chem Phys 123:204724

    Article  Google Scholar 

  4. Garcia-Sanchez P, Ramos A, Green G et al (2006) IEEE Trans Dielectr Electr Insul 13:670

    Article  CAS  Google Scholar 

  5. Green NG, Ramos A, Gonzalez A et al (2002) Phys Rev E 66:026305

    Article  CAS  Google Scholar 

  6. Mpholo M, Smith CG, Brown ABD (2003) Sens Actuators B 92:262

    Article  Google Scholar 

  7. Studer V, Pepin A, Chen Y et al (2004) Analyst 129:944

    Article  CAS  Google Scholar 

  8. Probstein RF (1994) Physicochemical hydrodynamics: an introduction. Wiley, New York

    Book  Google Scholar 

  9. Green NG, Ramos A, Morgan H (2000) J Phys D 33:632

    Article  CAS  Google Scholar 

  10. Bazant MZ, Ben YX (2006) Lab Chip 6:1455

    Article  CAS  Google Scholar 

  11. Burch D, Bazant MZ (2008) Phys Rev E 77:055303(R)

    Article  Google Scholar 

  12. Urbanski JP, Thorsen T, Levitan JA et al (2006) Appl Phys Lett 89:143508

    Article  Google Scholar 

  13. Urbanski JP, Levitan JA, Burch DN et al (2007) J Colloid Interface Sci 309:332

    Article  CAS  Google Scholar 

  14. Cahill BP, Heyderman LJ, Gobrecht J et al (2004) Phys Rev E 70:036305

    Article  Google Scholar 

  15. Cahill BP, Heyderman LJ, Gobrecht J et al (2005) Sens Actuators B 110:157

    Article  Google Scholar 

  16. Ramos A, Gonzalez A, Garcia-Sanchez P et al (2007) J Colloid Interface Sci 309:323

    Article  CAS  Google Scholar 

  17. Ejsing L, Smistrup K, Pedersen CM et al (2006) Phys Rev E 73:037302

    Article  CAS  Google Scholar 

  18. Mortensen NA, Olesen LH, Belmon L et al (2005) Phys Rev E 71:056306

    Article  Google Scholar 

  19. Ramos A, Morgan H, Green NG et al (2005) J Appl Phys 97:084906

    Article  Google Scholar 

  20. Squires TM, Bazant MZ (2004) J Fluid Mech 509:217

    Article  Google Scholar 

  21. Olesen LH, Bruus H, Ajdari A (2006) Phys Rev E 73:056313

    Article  Google Scholar 

  22. Kim BJ, Yoon SY, Sung H J et al (2007) J Appl Phys 102:074513

    Article  Google Scholar 

  23. Loucaides N, Ramos A, Georghiou GE (2007) Microfluid Nanofluid 3:709

    Article  Google Scholar 

  24. Khan T, Reppert PM (2005) J Colloid Interface Sci 290:574

    Article  CAS  Google Scholar 

  25. Wang XM, Wu JK (2006) J Colloid Interface Sci 293:483

    Article  CAS  Google Scholar 

  26. Pribyl M, Snita D, Marek M (2008) Multiphysical modeling of DC and AC electroosmosis in micro- and nanosystems. In: Petrone G, Cammarata G (eds) Recent advances in modelling and simulation. I-Tech Education and Publishing, Vienna

  27. Cervenka P, Pribyl M, Snita D (2009) Microelectron Eng 86:1333

    Article  CAS  Google Scholar 

  28. Kilic MS, Bazant MZ, Ajdari A (2007) Phys Rev E 75:021502

    Article  Google Scholar 

  29. Kilic MS, Bazant MZ, Ajdari A (2007) Phys Rev E 75:021503

    Article  Google Scholar 

  30. Storey BD, Edwards L R, Kilic MS et al (2008) Phys Rev E 77:036317

    Article  Google Scholar 

  31. Levitan JA, Devasenathipathy S, Studer V et al (2005) Colloids Surf A 267:122

    Article  CAS  Google Scholar 

  32. González A, Ramos A, Green NG et al (2000) Phys Rev E 61:4019

    Article  Google Scholar 

  33. Postler T, Slouka Z, Svoboda M et al (2008) J Colloid Interface Sci 320:321

    Article  CAS  Google Scholar 

  34. Deen WM (1998) Analysis of transport phenomena. Oxford University Press, New York

    Google Scholar 

Download references

Acknowledgements

The authors thank for the support by the grant of the GAAV ČR (KAN208240651), by the grant of the MŠMT ČR (MSM 6046137306), by the grant MPO ČR (Pokrok 1H-PK/24), and by the grant GAČR (GD 104/08/H055).

Author information

Authors and Affiliations

  1. Department of Chemical Engineering, Institute of Chemical Technology, Prague, Technická 5, 166 28, Prague 6, Czech Republic

    Jiří Hrdlička, Petr Červenka, Michal Přibyl & Dalimil Šnita

Authors
  1. Jiří Hrdlička
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Petr Červenka
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Michal Přibyl
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Dalimil Šnita
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Michal Přibyl.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Hrdlička, J., Červenka, P., Přibyl, M. et al. Mathematical modeling of AC electroosmosis in microfluidic and nanofluidic chips using equilibrium and non-equilibrium approaches. J Appl Electrochem 40, 967–980 (2010). https://doi.org/10.1007/s10800-009-9966-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10800-009-9966-3

Keywords

Search

Navigation