Abstract
We provide a generalization and adaptation of the decomposition methodology by Pfähler (Bull Econ Res 42:121–129, 1990) and Lambert (The distribution and redistribution of income, 1st edn, 1989, The distribution and redistribution of income, 3rd edn, 2001), designed to assess the redistributive effect of personal income taxation. In particular, we generalize the methodology to several deductions, allowances, schedules or tax credits, making it suitable for real-world complex tax structures, especially dual income taxes. Additionally, we avoid the problem of sequentiality on the measurement of partial redistributive effects and also take into account the re-ranking effects of tax treatments not related to income. Finally we illustrate the utility of the methodology by carrying out an empirical analysis for the 2007 Spanish Personal Income Tax, which meant a shift from a quasi-comprehensive to a semi-dual income tax.
Similar content being viewed by others
Notes
Since the late 1990s, the Shapley value technique has become an attractive solution to avoid sequential-dependency problems that arise in the decomposition of inequality. As far as we know, Shapley decomposition has not yet been used to quantify the redistributive impact of the constituent elements of the personal income, even though we believe that in the future, it might be an outstanding field of theoretical and applied research. An interesting reference on the possibilities and limitations of this methodology is Deutsch and Silber (2008).
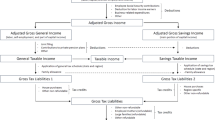
Detailed explanations on the homogenization and simplification of the original equations can be found in Onrubia et al. (2013).
We assume this because Lambert does not mention tax credits, but it might also be interpreted that he provides in a single figure the joint effect of tax rates and tax credits.
The opposite example would be a case where everybody could apply both the allowance and the deduction: Lambert’s approach would give identical redistributive effect for both measures, while Pfähler’s approach would conclude that the allowance is much more redistributive than the deduction.
Wagstaff et al. (2001) also use gross income, but their methodology is not applicable here because they only measure progressivity, not redistribution.
For example, if the redistributive effect of the tax base and the tax schedule is X, and the effect of tax credits is Y, if we remove the tax credits the effect of the tax would be just X. This does not happen in Pfähler and Urban approaches.
In the appendix, we prove that the parts of Eq. 8 add up the Reynolds–Smolensky index.
For a detailed description of the Spanish PIT Returns Panel see Onrubia and Picos-Sánchez (2011).
See above footnote 3 on the importance of this caveat.
Actually the differences may not be statistically significant. The use of confidence intervals would solve this issue, but their calculation is beyond the scope of this paper given the illustrative purpose of the calculations.
References
Dardanoni, V., & Lambert, P. J. (2002). Progressivity comparisons. Journal of Public Economics, 86(1), 99–122.
Decoster, A., Standaert, I., Valenduc, C., & Van Camp, G. (2002). What makes personal income taxes progressive? The case of Belgium. Brussels Economic Review—Cahiers Economiques de Bruxelles, 45(3), 91–112.
Deutsch, J., & Silber, J. (2008). On the Shapley value and the decomposition of inequality by subgroups with special emphasis on the Gini index”. In G. Betti & A. Lemmi (Eds.), Advances on income inequality and concentration measures. London: Routledge.
Kakwani, N. C. (1977). Measurement of tax progressivity: An international comparison. The Economic Journal, 87, 71–80.
Kakwani, N. C. (1984). On the measurement of tax progressivity and redistributive effect of taxes with applications to horizontal and vertical equity. Advances in Econometrics, 3, 149–168.
Kakwani, N., & Lambert, P. J. (1998). On measuring inequity in taxation: A new approach. European Journal of Political Economy, 14(2), 369–380.
Keen, M., Papapanagos, H., & Shorrocks, A. (2000). Tax reform and progressivity. The Economic Journal, 110, 50–68.
Kristjánsson, A. S. (2013). Redistributive effects of taxation in a dual income tax system. Finanzarchiv, 69(2), 148–166.
Lambert, P. J. (1989). The distribution and redistribution of income (1st ed.). Oxford: Basil Blackwell.
Lambert, P. J. (2001). The distribution and redistribution of income (3rd ed.). Manchester: Manchester University.
Onrubia, J. & Picos-Sánchez, F. (2011). The 1999–2007 Spanish income tax return panel: Design and applications. Paper presented at the 3rd General Conference of the International Microsimulation Association, Stockholm, Sweden, June 8–10, 2011.
Onrubia, J., Picos-Sánchez, F. & Rodado, M.C. (2013). A generalization of the Pfähler-Lambert decomposition. International Center for Public Policy Working Paper Series, 13–01.
Pfähler, W. (1990). Redistributive effect of income taxation: Decomposing tax base and tax rates effects. Bulletin of Economic Research, 42, 121–129.
Seidl, C. (1994). On the measurement of tax progressivity with nonconstant income distributions. In W. Eichhorn (Ed.), Models and measurement of welfare and inequality (pp. 337–360). Berlin: Springer Verlag.
Seidl, C., Pogorelskiy, K., & Traub, S. (2013). Tax progression in OECD countries. An integrative analysis of tax schedules and income distributions. Berlin: Springer Verlag.
Urban, I. (2006). Progressivity of personal income tax in Croatia: Decomposition of tax base and rate effects. Financial Theory and Practice, 30(3), 207–231.
Verbist, G. (2004). Redistributive effect and progressivity of taxes: An international comparison across the EU using EUROMOD. EUROMOD Working Paper Series, No. EM5/04.
Wagstaff, A., Van Doorslaer, E., Van Der Burg, H., Calonge, S., Christiansen, T., Citoni, G., et al. (1999). Redistributive effect, progressivity and differential tax treatment: Personal income taxes in twelve OECD countries. Journal of Public Economics, 72(1), 73–98.
Wagstaff, A., & van Doorslaer, E. (2001). What makes the personal income tax progressive? A comparative analysis for fifteen OECD countries. International Tax and Public Finance, 8(3), 299–316.
Acknowledgments
Earlier versions of this paper were presented at the 20th Public Economics Meeting on Public Economics (Seville, Spain, January 31–February 1 2013) and at the 69th Annual Congress of the IIPF (Taormina, Sicily, Italy, August 21–25 2013). We gratefully acknowledge the useful comments and suggestions received from Peter J. Lambert, Julio López-Laborda, Alessandro Sommacal and the participants in the abovementioned meetings. We also thank three anonymous referees. Any remaining errors are entirely our responsibility. We also thank the International Center for Public Policy (Georgia State University) for publishing an earlier version of this paper in its Working Paper series. Jorge Onrubia and M. Carmen Rodado thank the Spanish Ministry of Economy and Competitiveness (IV National Plan of Scientific Research, Development and Technology Innovation, Project ECO2012-37572). Fidel Picos-Sánchez acknowledges the financial support from Xunta de Galicia (‘Programa de Consolidación e Estruturación de Unidades de Investigación Competitivas’) and the European Regional Development Fund (ERDF).
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
We take Eq. 2 (Lambert’s version) as a starting point:
The first step is generalizing the split between allowance and deductions to \(n\) allowances and deductions (for simplicity we only use the word deductions, D):
Using the same procedure, we now generalize the first term to l different tax schedules, assuming that the overall tax liability is a sum of partial tax liabilities (\(S=S_1 +S_2 +\cdots +S_\mathrm{l} )\):
Since this equation does not provide the effect of tax credits, we include it at the end of the equation just by adding the redistribution induced by the tax credits expressed by a partial Reynolds–Smolensky index:
Now we also generalize the new term for \(m\) tax credits, as we did with deductions and schedules:
Since Lambert’s formula does not include the re-ranking effect we just add it to obtain the Reynolds–Smolensky index:
which is actually Eq. 8.
Rights and permissions
About this article
Cite this article
Onrubia, J., Picos-Sánchez, F. & del Carmen Rodado, M. Rethinking the Pfähler–Lambert decomposition to analyse real-world personal income taxes. Int Tax Public Finance 21, 796–812 (2014). https://doi.org/10.1007/s10797-014-9316-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10797-014-9316-1