Abstract
In this paper we treat an individual’s health as a continuous variable, in contrast to the traditional literature on income insurance, where it is assumed that the individual is either able or unable to work. A continuous treatment of an individual’s health sheds new light on the role of income insurance and makes it possible to capture a number of real-world phenomena that are not easily captured in the traditional, dichotomous models. In particular, we show that moral hazard is not necessarily outright fraud, but a gradual adjustment of the willingness to work, depending on preferences and the conditions stated in the insurance contract. Further, the model can easily encompass phenomena such as administrative rejection of claims, and it clarifies the conditions for the desirability of insurance in the first place.



Similar content being viewed by others
Notes
The general, non-linear income tax system of Mirrlees (1971) may be interpreted as an insurance system, where the insurer has information about the individual’s income, but not about the realization of his productivity.
Diamond (2003, Chap. 6) also uses a continuous approach to analyze the design of optimal retirement incentives. Moreover, Engström and Holmlund (2007) use a continuous representation of the individual’s health when asking whether the benefit levels in unemployment and sick-pay insurance should differ or be the same. Outside the insurance literature, there are several papers on absence from work using a utility function with a continuous index variable reflecting the individual’s health status; see the survey by Brown and Sessions (1996).
The traditional, dichotomous framework means that θ can take only two values, one of which is so negative (for instance, −∞) that the individual is completely unable to work.
There is a literature on how the marginal utility of consumption is influenced by the individual’s health; see for instance Kremslehner and Muermann (2009) and Finkelstein et al. (2009). This literature often asserts that the cross derivative u cθ is positive. However, it could well be argued that the cross derivative is negative. It is true that if you are sick, your marginal utility of many consumption goods (food, cars, vacation trips) is low. But on the other hand, your marginal utility of certain other consumption goods might be very high. Obvious examples are nursing services, medical equipment, wheelchairs, etc. It should also be noticed that in contrast to this literature, the stochastic variable θ in our model enters the utility function only when the individual works; when he chooses not to work, his utility function is u(c).
Here, the “zero” does not necessarily mean that the individual is subject to starvation when not working. He may have other resources than labor income to support himself; these are suppressed in the notation u(⋅).
Dropping additive separability, we have u(c,θ). Instead of (3), the cut-off is then given by \(u(1, \theta_{0}^{ *} ) = u(0, 0)\). Provided that u(c,θ) is monotone in both arguments, the solution \(\theta_{0}^{ *} < 0\) is unique.
With a non-separable utility function u(1+ψ(θ,1),θ) when working and u(ψ(θ,0),0) when not working, the optimal benefit under full observability should still be independent of θ while the optimal premium should vary with θ.
There are some similar results concerning the desirability of insurance in other strands of the literature. In the case of sick care insurance, assuming a dichotomous distribution of health, Strohmenger and Wambach (2000) analyze whether there exists some probability of sickness for which such insurance is not desirable, and show that an individual with concave consumption utility may abstain from buying insurance. Moreover, in the case of insurance of irreplaceable commodities (such as family heirloom, and the like) Cook and Graham (1977) point out the possibility that an individual may choose not to buy insurance. That result is driven by the assumption that money cannot compensate for irreplaceable losses (i.e., that there is a cross derivative u cθ >0).
Cf. Rothschild and Stiglitz (1976).
With a non-separable utility function, the inequality corresponding to u′(1)≥u′(0) becomes \(u_{1}(0, 0) \le E(u_{1}(1, \theta) | \theta> \theta_{0}^{ *} )\). Whether this inequality is consistent with a concave utility function depends not only on the distribution of θ, as in the case of a separable utility function, but also on the cross derivative u 12 (which may be positive or negative).
Condition (ii) in Proposition 3 is not necessary, but only sufficient. Even individuals who always work in the absence of insurance (i.e., individuals with \(\theta_{\mathrm{lower}} > \theta_{0}^{ *}\)) may be willing to buy insurance to be able to stay home for relatively unfavorable realizations of θ.
With utility u(c,θ), the cut-off in the absence of insurance is given by \(u(0, 0) = u(1, \theta_{0}^{ *} )\). Condition (10) then is \(u(b_{N}, 0) = u(1 - p_{N}, \hat{\theta}_{N})\). Since the left-hand side of the latter equation is larger than the left-hand side of the former, and since 1−p N <1, it must hold that \(\hat{\theta}_{N} > \theta_{0}^{ *}\). Hence, the introduction of insurance leads to a fall in labor supply also with non-separable utility.
In the Diamond and Mirrlees (1978) model, the disutility of work is infinite for a sick individual. In this sense, the tax wedge p+b does not bite in that model. In other dichotomous models, disutility of work may be finite. In both cases, aggregate labor supply will be a step function.
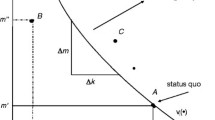
It is easy to prove that the indifference curves are upward-sloping, as shown in the figure. This also holds for non-separable utility functions. Although we have depicted the curves as convex, they may contain both concave and convex segments. Such an ambiguity concerning the curvature of indifference curves is found also in other strands of the insurance literature; cf. Stiglitz (1983) and Arnott (1992).
It can be shown that a sufficient condition for the zero-profit constraint to look like a well-behaved Laffer curve, with a unique maximum, is that F(θ ∗)/(1−F(θ ∗)) is an increasing, convex function of θ ∗. This property characterizes many distribution functions, although there are some exceptions (for instance, a Student’s t distribution with less than one “degree of freedom”, i.e., with thick tails and an infinite mean).
More specifically, the Prescott and Townsend (1984) lottery implies that with probability π 1, you should work h 1 hours, and with probability π 2, you should work h 2 hours, regardless of your health status. If e.g. h 2 is very large, that outcome of the lottery may be impossible to implement in a society with no slave labor.
By definition, all lotteries violate the principle of horizontal equity. Nevertheless, the world is full of lotteries, in many cases sponsored by the government. We return to the issue of rejection of claims in a more realistic framework in Sect. 5.
For instance, we have studied the consequences of variations in k>0. It turns out that with our parameterization, q is a decreasing function of k.
By “plausible” we mean values that are of an order of magnitude similar to those observed in the real world. In the simulations reported in Fig. 2, the absence rate, as given by (13), varies between 0.2 and 0.25. This is a realistic figure for many European countries if both sick-pay insurance and disability pensions are included.
Thus, in our lottery, we do not eliminate the individual’s freedom of choice: after the lottery has been executed, the individual is free to decide whether he should work or not. This contrasts to the work-assignment lottery in the paper by Prescott and Townsend (1984) mentioned in footnote 17 above; in that lottery, the individual is obliged to perform the number of hours of work specified by the outcome of the lottery.
In the standard dichotomous model, a rejection rate can never increase expected utility. The reason is that there is no heterogeneity among those who apply for benefits in the case of an optimum contract; they are all unable to work.
An interesting topic for future study is a contract where the size of the benefit may vary with the signal s=θ+ε (the contribution cannot vary with the signal, since the premium has to be paid in advance).
The conditions are similar to the condition for a moral-hazard problem to emerge in the dichotomous model under non-observability of Diamond and Mirrlees (1978).
The proof is parallel to that of Proposition 8 above and is therefore not reported here.
References
Arnott, R. J. (1992). Moral hazard and competitive insurance markets. In G. Dionne (Ed.), Contributions to insurance economics (pp. 325–359). Boston: Kluwer Academic.
Brown, S., & Sessions, J. G. (1996). The economics of absence: theory and evidence. Journal of Economic Surveys, 10(1), 23–53.
Cook, P. J., & Graham, D. A. (1977). The demand for insurance and protection: the case of irreplaceable commodities. Quarterly Journal of Economics, 91(1), 143–156.
Diamond, P. A. (2003). Taxation, incomplete markets, and social security. The 2000 Munich lectures. Cambridge: MIT Press.
Diamond, P. A., & Mirrlees, J. A. (1978). A model of social insurance with variable retirement. Journal of Public Economics, 10(3), 295–336.
Diamond, P. A., & Sheshinski, E. (1995). Economic aspects of optimal disability benefits. Journal of Public Economics, 57(1), 1–23.
Engström, P., & Holmlund, B. (2007). Worker absenteeism in search equilibrium. Scandinavian Journal of Economics, 109(3), 439–467.
Finkelstein, A., Luttmer, E., & Notowidigdo, M. (2009). Approaches to estimating the health state dependence of the utility function. American Economic Review: Papers and Proceedings, 99(2), 116–121.
Golosov, M., & Tsyvinski, A. (2006). Designing optimal disability insurance: a case for asset testing. Journal of Political Economy, 114(2), 257–279.
Kremslehner, R., & Muermann, A. (2009). State-dependent preferences and insurance demand. Vienna university of economics and business. Working paper. http://ssrn.com/abstract=1466719 or doi:10.2139/ssrn.1466719.
Mirrlees, J. A. (1971). An exploration in the theory of optimum income taxation. Review of Economic Studies, 38(2), 175–208.
Prescott, E. C., & Townsend, R. M. (1984). Pareto optima and competitive equilibria with adverse selection and moral hazard. Econometrica, 52(1), 21–45.
Rees, R. (1989). Uncertainty, information and insurance. In J. D. Hey (Ed.), Current issues in microeconomics, London: Macmillan.
Rees, R., & Wambach, A. (2008). The microeconomics of insurance. Foundations and Trends in Microeconomics, 4(1–2), 1–163.
Rothschild, M., & Stiglitz, J. E. (1976). Equilibrium in competitive insurance markets: an essay on the economics of imperfect information. Quarterly Journal of Economics, 90(4), 629–649.
Stiglitz, J. E. (1983). Risk, incentives and insurance: the pure theory of moral hazard. The Geneva Papers on Risk and Insurance. Issues and Practice, 8(26), 4–33.
Strohmenger, R., & Wambach, A. (2000). Adverse selection and categorical discrimination in the health insurance markets: the effects of genetic tests. Journal of Health Economics, 19(2), 197–218.
Whinston, M. D. (1983). Moral hazard, adverse selection, and the optimal provision of social insurance. Journal of Public Economics, 22(1), 49–71.
Zweifel, P. (2007). The theory of social health insurance. Foundations and Trends in Microeconomics, 3(3), 183–273. Adverse selection and categorical discrimination in the health insurance markets.
Acknowledgements
We are grateful to Per Engström, Mathias Herzing, Harald Lang, Tomas Sjöström, Johan Stennek and Jens Svensson for valuable comments and suggestions on an earlier version of this paper. Assar Lindbeck gratefully acknowledges research support from The Catarina and Sven Hagströmer Foundation.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Proofs
Proof of Proposition 1
Condition (i) in the proposition is necessary since if \(\theta_{\mathrm{upper}} \le\hat{\theta}_{F} = - u'(1 - F(\hat{\theta}_{F}))\), no one will ever work in the presence of insurance and thus, \(F(\hat{\theta}_{F}) = 1\). In this case, the inequality can be written θ upper≤−u′(0) and no insurance can be financed. Thus, θ upper>−u′(0) is a necessary condition for insurance to be feasible. Condition (ii) in the proposition is also necessary since if \(\theta_{\mathrm{lower}} \ge\hat{\theta}_{F} = - u'(1 - F(\hat{\theta}_{F}))\), everyone will always work in the presence of insurance and thus insurance will not be utilized. In that case, \(F(\hat{\theta}_{F}) = 0\) and as a result the inequality can be written θ lower≥−u′(1). Thus, θ lower<−u′(1) is necessary for insurance to be desirable.
To prove sufficiency, we note that, by definition, an interior solution \(\hat{\theta}_{F}\) satisfies \(\theta_{\mathrm{lower}} < \hat{\theta}_{F} < \theta_{\mathrm{upper}}\). To prove that a utility function u and a distribution function F satisfying (i) and (ii) must also satisfy this inequality, we define the function φ(θ)≡θ+u′(1−F(θ)). We have φ(θ lower)=θ lower+u′(1) which, by (ii), is negative. We also have φ(θ upper)=θ upper+u′(0) which, by (i), is positive. The continuous and monotone function φ(θ) must therefore take the value of zero for one (unique) value of θ somewhere in the open interval (θ lower,θ upper). By (9), the φ(θ) is zero for \(\theta= \hat{\theta}_{F}\); thus \(\hat{\theta}_{F}\) is located in the interval (θ lower,θ upper). □
Proofs of some properties of optimal insurance in Sect. 5.2
(i) An optimal contract implies less than full insurance
The first-order conditions of the maximization of EU subject to the budget constraint, with respect to p and b, can be written
where
With an interior solution, these conditions are satisfied as equalities, implying that the weighted average of u′(1−p) and u′(−p) should be equal to the weighted average of u′(1+b) and u′(b). Since u′(−p)>u′(1+b), the two weighted averages can be equal only if u′(b)>u′(1−p), i.e., only if 1−p>b. □
(ii) The effects on labor supply are ambiguous
The introduction of insurance will induce some individuals with a lucky outcome to choose to stay home from work even though they would have gone to work in the absence of a lottery. These individuals will reduce their labor supply. The number of such individuals is \(\int_{ \theta _{0}^{ *}}^{ \tilde{\theta}} dF(\theta)\). Similarly, a number of individuals with a bad outcome in θ and bad luck in the lottery will choose to work, even though they would have stayed home in the absence of insurance; such individuals contribute to an increase in the labor supply. The number of these individuals is \(\int_{ \tilde{\tilde{\theta}}}^{\theta_{0}^{ *}} dF(\theta)\). Without adding more structure to the model, it is not possible to determine whether \(\int_{ \tilde{\tilde{\theta}}}^{\theta_{0}^{ *}} dF(\theta)\) is smaller or larger than \(\int_{ \theta_{0}^{ *}}^{ \tilde{\theta}} dF(\theta)\). □
(iii) Desirability of insurance
A necessary condition for insurance, based only on the signal s, to be desirable is that there is some mass between \(\tilde{\tilde{\theta}}\) and \(\tilde{\theta}\), where \(\tilde{\theta} \equiv u(b) - u(1 + b)\) and \(\tilde{\tilde{\theta}} \equiv u( - p) - u(1 - p)\). This condition is satisfied if there is some mass around \(\theta_{0}^{ *}\).
To prove this, we first note that \(\tilde{\tilde{\theta}} < \theta_{0}^{ *} < \tilde{\theta}\). Assume that all mass of the distribution is to the right of \(\tilde{\theta}\). Then everyone will always work, regardless of the outcome of the lottery. The lottery would thus only cause variability in income, and would therefore be undesirable to a risk-averse individual. Thus \(\theta_{\mathrm{lower}} < \tilde{\theta}\) is a necessary condition for the lottery to be desirable. Assume now that all mass of the distribution is to the left of \(\tilde{\tilde{\theta}}\). Then no one would ever work. In such a case, the lottery would only cause income variability, which is undesirable. Hence \(\theta_{\mathrm{upper}} > \tilde{\tilde{\theta}}\) is also a necessary condition for the lottery to be desirable. These two conditions combined imply that some mass between \(\tilde{\tilde{\theta}}\) and \(\tilde{\theta}\) is necessary for the lottery to be desirable. Since \(\tilde{\tilde{\theta}} < \theta_{0}^{ *} < \tilde{\theta}\), some mass around \(\theta_{0}^{ *}\) is sufficient for this to occur. □
Appendix B: Effects on labor supply of insurance under full observability
Under what conditions does the introduction of insurance result in a positive (b) or a negative (−p) income change, and hence a fall or an increase in labor supply? It depends on whether \(\theta_{0}^{ *} = u(0) - u(1)\) is larger than, or smaller than \(\hat{\theta}_{F} = - u'( 1 - F(\hat{\theta}_{F}) )\), which in turn depends on the u(⋅) and F(⋅) functions.
Assume first that \(\theta^{*}<\hat{\theta}_{F}\). The individual would earn 0 if not working, and 1 if working, in the absence of insurance. With insurance, and with a realization \(\theta^{*}<\theta<\hat{\theta}_{F}\), he would earn b if not working, and 1+b if working (since the benefit is not conditioned on his labor supply decision, but only on the realization θ). Thus, the introduction of insurance provides a positive income increase b regardless of whether the individual works or not. As a result, the individual will demand more pain relief, hence reducing his labor supply.
This reasoning applies for a realization \(\theta^{*}<\theta<\hat{\theta}_{F}\). For a realization outside that interval, the introduction of insurance will not have any effect on labor supply; an individual who does not work in the absence of insurance has even stronger reasons not to work when he gets an income transfer b. Correspondingly, an individual who works in the absence of insurance will have even stronger reasons to work when he is exposed to a lump-sum income reduction –p. The configuration \(\theta^{*}<\hat{\theta}_{F}\) therefore implies that the introduction of insurance will reduce aggregate labor supply.
Assume instead that \(\hat{\theta}_{F}<\theta^{*}\). As always, the individual would earn 0 if not working, and 1 if working, in the absence of insurance. With insurance, and with a realization \(\hat{\theta}_{F}<\theta<\theta^{*}\), he would earn –p if not working, and 1−p if working. Thus, the introduction of insurance provides a negative income change, regardless of whether the individual works or not. As a result, he will settle for less pain relief, hence increasing his labor supply.
This reasoning applies for a realization \(\theta^{*}<\theta<\hat{\theta}_{F}\). With the same argument as above for realizations outside the interval, we conclude that the configuration \(\hat{\theta}_{F}<\theta^{*}\) implies that the introduction of insurance will increase aggregate labor supply.
The analysis shows that under full observability, the effect of insurance on labor supply is driven only by exogenous lump-sum changes in income, and not by any price distortions. These lump-sum changes are positive or negative, depending on the u(⋅) and F(⋅) functions.
Rights and permissions
About this article
Cite this article
Lindbeck, A., Persson, M. A continuous model of income insurance. Int Tax Public Finance 20, 938–960 (2013). https://doi.org/10.1007/s10797-012-9253-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10797-012-9253-9