Skip to main content
SpringerLink
Log in

Nonlinear Deformation of Discretely Inhomogeneous Shallow Shells Based on the Generalized Method of Finite Integral Transforms*

  • Published:
International Applied Mechanics Aims and scope

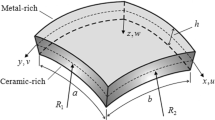
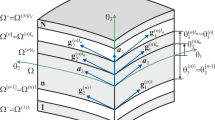
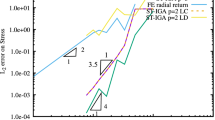
A numerical analytical approach to the study of the nonlinear deformation of shallow shells under subcritical loads is proposed. The approach rationally combines the generalized method of finite integral transforms and the Newton–Kantorovich–Raphson linearization method. The static stiffness and load–deflection relationship of flexible shallow shells with various boundary conditions in a wide range of changes in their Gaussian curvature and the presence of discrete inclusions are analyzed. It is shown that the dependence of the upper critical values of external pressure on the location of discrete inclusions is nonmonotonic, which makes it possible to determine their optimal location in terms of the static stability and bearing capacity of the shells.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. V. A. Bazhenov, N. A. Solovei, and O. P. Krivenko, “Stability of shallow shells of revolution with linearly variable thickness,” Aviats.-Kom. Tekhn. Tekhnol., 10, No. 2, 18–25 (2004).

    Google Scholar 

  2. R. E. Bellman and R. E. Kalaba, Quasilinearization and Nonlinear Boundary-Value Problems, Elsevier, New York (1965).

    MATH  Google Scholar 

  3. Ya. M. Grigorenko, E. I. Bespalova, A. B. Kitaigorodskii, and A. I. Shinkar’, “Numerical solution of nonlinear boundary-value problems of the statics of flexible shells,” Dokl. AN USSR, Ser. A, No. 6, 44–48 (1986).

  4. M. S. Kornishin, Nonlinear Problems in the Theory of Plates and Shallow Shells and Methods to Solve Them [in Russian] Nauka, Moscow (1964).

  5. N. S. Koshliakov, E. B. Gliner, and M. M. Smirnov, Main Differential Equations of Mathematical Physics [in Russian], Fizmatgiz, Moscow (1962).

    Google Scholar 

  6. O. P. Kryvenko, “The effect of heating on the stability and natural vibrations of a spherical panel upon changes in the combined boundary conditions,” Opir Mat. Teor. Sporud, No. 96, 48–64 (2015).

  7. Yu. E. Senitskii, “Finite integral transform method: Generalization of the classical procedure of expansion into series of vector eigenfunctions,” Izv. Saratov. Univ., Ser. Mat. Mekh. Inform., No. 3 (1), 61–89 (2011).

  8. M. Amabili, “Nonlinear vibrations and stability of doubly curved shallow-shells: isotropic and laminated materials,” in: Nonlinear Vibrations and Stability of Shells and Plates, Cambridge University Press (2008), pp. 272–297.

  9. J. Awrejcewicz, L. Kurpa, and T. Shmatko, “Analysis of geometrically nonlinear vibrations of functionally graded shallow shells of a complex shape,” Lat. Am. J. Solids Struct., 9, No. 14, 1648–1668 (2017).

    Article  Google Scholar 

  10. E. I. Bespalova, “On the method of finite integral transforms in problems of statics of inhomogeneous plates,” Int. Appl. Mech., 50, No. 6, 651–663 (2014).

    Article  MATH  Google Scholar 

  11. E. I. Bespalova, “Generalized method of finite integral transforms in static problems for anisotropic prisms,” Int. Appl. Mech., 54, No. 1, 41–55 (2018).

    Article  MathSciNet  MATH  Google Scholar 

  12. E. Bespalova and G. Urusova, “Solution of the lame problem by the complete systems method,” Int. J. for Comp. Meth. Eng. Sci. Mech., 14, No. 2, 159–167 (2013).

  13. D. H. Campen, V. P. Bouwman, G. Q. Zhang, J. Zhang, and B. J. W. Weeme, “Semi-analytical stability analysis of doubly-curved orthotropic shallow panels-considering the effects of boundary conditions,” Int. J. of Non-Lin. Mech., 37, No. 4–5, 659–667 (2002).

    Article  MATH  Google Scholar 

  14. N. D. Duc and T. Q. Quan, “Nonlinear stability analysis of double-curved shallow fgm panels on elastic foundations in thermal environments,” Mech. Comp. Mater., 48, No. 4, 435–448 (2012).

    Article  Google Scholar 

  15. A. Garg, H. D. Chalak, M. O. Belarbi, A. M. Zenkour, and R. Sahoo, “Estimation of carbon nanotubes and their applications as reinforcing composite materials – an engineering review,” Comp. Struct., No. 272, 114234 (2021).

  16. Ya. M. Grygorenko and L. S. Rozhok, “Analysis of stress state of hollow orthotropic cylinders with oval cross-section,” Int. Appl. Mech., 57, No. 2, 45–57 (2021).

    Google Scholar 

  17. S. Huang and P. Qiao, “A new semi-analytical method for nonlinear stability analysis of stiffened laminated composite doubly-curved shallow shells,” Comp. Struct., 251, No. 1.112526 (2020).

  18. R. Kumar, L. S. Ramachandra, and B. Banerjee, “Nonlinear stability characteristics of composite cylindrical panel subjected to non-uniform in-plane mechanical and localized thermal loadings,” Proc. Ind. Nat. Sci. Acad., 82, No. 2, 271–288 (2016).

    Google Scholar 

  19. S. Kurukuri, “Stability and geometrical nonlinear analysis of shallow shell structures,” Adv. Mech. of Mat. and Struct. Grad. School of Struct. Eng. Project-2, Bauhaus Universität, Weimar, 1–46 (2004).

  20. M. Psotny and J. Havran, “Stability analysis of an open shallow cylindrical shell with imperfection under external pressure,” in: MATEC Web of Conferences, Slovak University of Technology, Bratislava (2017), pp. 1–6.

  21. D. P. Roberts, “Numerical modelling of blocky and stratified hangingwall behaviour,” in: 6-th Int. Symposium on Ground Support in Mining and Civil Engineering Construction, SAIMM, SANIRE and ISRM (2008), pp. 329–344.

  22. N. P. Semenyuk and N. B. Zhukova, “Stability of a sandwich cylindrical shell with core subject to external pressure and pressure in the inner cylinder,” Int. Appl. Mech., 56, No. 1, 40–53 (2020).

    Article  MathSciNet  MATH  Google Scholar 

  23. N. P. Semenyuk and N. B. Zhukova, “Effect of mechanical and geometric parameters of composite cylindrical shells with localized deflection on character of equilibrium curves under axial compression,” Int. Appl. Mech., 57, No. 1, 75–87 (2021).

    Article  Google Scholar 

  24. B. P. Watson and R. Gerber, “Determination of stable spans in UG2 excavations,” J. of the South. Afric. Inst. of Min. and Met., 118, No. 5, 493–504 (2018).

  25. J. Z. Zhang and D. H. van Campen, “Stability and bifurcation of doubly curved shallow panels under quasi-static uniform load,” Int. J. of Non-Lin. Mech., 38, No. 4, 457–466 (2003).

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. S. P. Timoshenko Institute of Mechanics, National Academy of Sciences of Ukraine, 3 Nesterova St, Kyiv, 03057, Ukraine

    O. I. Bespalova

Authors
  1. O. I. Bespalova
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to O. I. Bespalova.

Additional information

Translated from Prykladna Mekhanika, Vol. 58, No. 5, pp. 81–96, September–October 2022

This study was sponsored by the budget program “Support for Priority Areas of Scientific Research” (KPKVK 6541230).

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bespalova, O.I. Nonlinear Deformation of Discretely Inhomogeneous Shallow Shells Based on the Generalized Method of Finite Integral Transforms*. Int Appl Mech 58, 569–582 (2022). https://doi.org/10.1007/s10778-023-01181-6

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10778-023-01181-6

Keywords

Search

Navigation