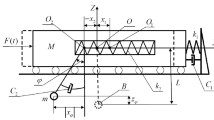
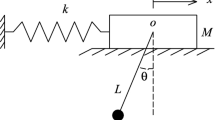
A mathematical model describing the forced oscillations of the vibration protection system with a pendulum damper of new design with a mobile suspension point is constructed. The model is a system of nonlinear differential equations. After the linearization of this system, the frequency response of the system is established. The model is used to derive a frequency formula for small natural oscillations of a pendulum. The main adjustment parameters of the damper that affect its optimal adjustment are established. A numerical analysis of the dynamic behavior of the vibration protection system shows the high efficiency of the pendulum damper. With the optimal adjustment of the damper parameters, the amplitudes of the forced oscillations of the carrying body can be reduced to one fifth the initial value.
Similar content being viewed by others
References
I. A. Vikovich, B. M. Diveev, and V. E. Martin, “Use of various types of pendulum dynamic vibration dampers,” Visn. Nats. Transp. Univ., No. 29 (1), 26–33 (2014).
DBN B.1.2-2:2006. Loads and Effects. Design Standards [in Ukrainian], Minbud Ukrainy, Kyiv (2006).
B. G. Korenev and I. M. Rabinovich (eds.), Dynamic Design of Buildings and Other Structures: Designer’s Handbook [in Russian], Stroiizdat, Moscow (1984).
V. P. Legeza, Theory of Vibration Protection of Systems with Isochronous Roller Dampers (Models, Methods, Dynamic Analysis, Engineering Solutions) [in Russian], Lambert Academic Publishing, Saarbrücken, Deutschland (2013).
V. P. Legeza, I. A. Dychka, and Ya. V. Bovkun, “Suppression of vibrations of conductors and cables with use of a two-mass pendulum damper,” Elektr. Sist. Seti, No. 2, 7–13 (2016).
B. V. Ostroumov, “Dynamic inverted-pendulum damper of vibrations,” Izv. Vyssh. Uch. Zaved. (Stroit.), No. 9, 36–38 (2002).
Applied Technology Council (ATC), Seismic Evaluation and Retrofit of Concrete Buildings, ATC-40, Redwood City, CA (1996).
ASCE 41-06, Seismic Rehabilitation of Existing Buildings, Amer. Soc. of Civil Engineers, Reston (2007).
J. M. W. Brownjohn and T. C. Pan, “Response of tall building to weak long distance earthquakes,” Earthquake Eng. Struct. Dynam., 30, 709–729 (2001).
C. C. Chang and W. L. Qu, “Unified dynamic absorber design formulas for wind-induced vibration control of tall buildings,” Struct. Design Tall Buildings, 7, No. 2, 147–166 (1998).
C. C. Chang, “Mass dampers and their optimal designs for building vibration control,” Eng Struct., 21, No. 5, 454–463 (1999).
T. Dahlberg, “On optimal use of the mass of a dynamic vibration absorber,” J. Sound Vibr., 132, No. 3, 518–522 (1989).
J. P. Den Hartog, Mechanical Vibrations, Dover, New (2013).
Murty K. S. Madugula (ed.), Dynamic Response of Lattice Towers and Guyed Masts, Amer. Soc. Civil Engineers, Reston (2002).
R. R. Gerges and B. J. Vickery, “Wind tunnel study of the across-wind response of a slender tower with a nonlinear tuned mass damper,” J. Wind, 91, No. 8, 1069–1092 (2003).
S. Graham Kelly, Mechanical Vibrations: Theory and Applications, Cengage Learning (2012).
Z. Hu, V. Legeza, I. Dychka, and M. Onai, “Non-linear model of the damping process in a system with a two-mass pendulum absorber,” Int. J. Intelligent Systems and Applications (IJISA), 11, No. 1, 67–72 (2019).
I. A. Karnovsky and E. Lebed, Theory of Vibration Protection, Springer, Berlin (2016).
B. G. Korenev and L. M. Reznikov, Dynamic Vibration Absorbers: Theory and Technical Applications, John Wiley and Sons, Chichester (1993).
C. L. Lee, Y. T. Chen, L. L. Chung, and Y. P. Wang, “Optimal design theories and applications of tuned mass dampers,” Eng. Struct., 28, No. 1, 43–53 (2006).
A. Y. T. Leung and H. J. Zhang, “Particle swarm optimization of tuned mass dampers,” Eng. Struct., 31, No. 3, 715–728 (2009).
A. I. Lurie, Analytical Mechanics, Springer, Berlin (2002).
Sagar Jamle, Kundan Meshram, and Rajesh Chouhan, “Dynamic analysis of tuned mass damper on steel structure,” A Technical Approach, IJRAR, 6, No. 2, 956–960 (2019).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Prykladna Mekhanika, Vol. 58, No. 3, pp. 91–101, May–June 2022.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Legeza, V.P. Dynamic Analysis of the Behavior of a Pendulum Damper with Mobile Suspension Point. Int Appl Mech 58, 327–335 (2022). https://doi.org/10.1007/s10778-022-01158-x
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10778-022-01158-x