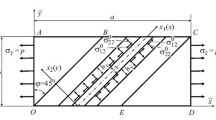
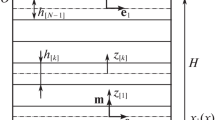
A numerical solution of the problem of determining the buckling in the structure of a composite material weakly reinforced with near-surface short fibers under compression along the direction of reinforcement is obtained. The basic relations of the three-dimensional linearized stability theory and the piecewise-homogeneous medium model are used. The subcritical state associated with the initial curvature of the fibers is studied, and the dependence of the buckling modes in the structure of the composite material on the location of the fibers relative to the free surface and the distance between adjacent fibers is determined. The mesh-based method based on a modified variational-difference approach is used to solve the problem numerically. The consecutive and parallel algorithms of the Kholetsky methods and subspace iteration are applied.
Similar content being viewed by others
References
V. M. Bistrov, V. A. Dekret, and V. S. Zelenskyi, “The buckling of a composite material weakly reinforced with near-surface short fibers,” in: Problems of Computational Mechanics and Strength of Structures [in Ukrainian], Issue 31 (2020), pp. 19–30.
A. N. Guz, Fundamentals of the Three-Dimensional Theory of Stability of Deformable Bodies [in Russian], Vyshcha Shkola, Kyiv (1986).
A. N. Guz, Structural Failure of Materials, Vol. 1 of the two-volume series Fundamentals of the Fracture Mechanics of Compressed Composites [in Russian], Litera, Kyiv (2008).
A. N. Guz and V. A. Dekret, Short-Fiber Model in the Theory of the Stability of Composites [in Russian], LAP Lambert Acad. Publ., Saarbrücken (2015).
Ya. M. Grigorenko, Yu. N. Shevchenko, A. T. Vasilenko, et al., Numerical Methods, Vol. 11 of the 12-volume series Mechanics of Composite Materials [in Russian], A.S.K., Kyiv (2002).
B. N. Parlett, The Symmetric Eigenvalue Problem, Prentice-Hall, Englewood Cliffs (1980).
S. Pissanetzky, Sparse Matrix Technology, Academic Press (1984).
A. V. Popov and A. N. Khimich, “Parallel algorithm for solving a system of linear algebraic equations with a symmetric banded matrix,” Komp. Mat., No. 2, 52–59 (2005).
O. M. Khimich and A. Yu. Baranov, “Hybrid algorithm for solving linear systems with banded matrices by direct methods,” Komp. Mat., No. 2, 80–87 (2013).
A. N. Khimich, I. N. Molchanov, A. V. Popov, T. V. Chistyakova, and M. F. Yakovlev, Parallel Algorithms for Solving Problems of Computational Mathematics [in Russian], Naukova Dumka, Kyiv (2008).
V. M. Bystrov, V. A. Dekret, and V. S. Zelenskii, “Loss of stability in a composite laminate compressed by a surface load,” Int. Appl. Mech., 53, No. 2, 156–163 (2017).
V. M. Bystrov, V. A. Dekret, and V. S. Zelenskii, “Numerical analysis of the edge effect in a composite laminate with compressed reinforcement plies,” Int. Appl. Mech., 51, No. 5, 561–566 (2015).
A. N. Guz, Fundamentals of the Three-Dimensional Theory of Stability of Deformable Bodies, Springer-Verlag Heilberg, Berlin (1999).
A. N. Guz, “Nonclassical problems of fracture/failure mechanics: on the occasion of the 50th anniversary of the research (review) II,” Int. Appl. Mech., 55, No. 3, 239–295 (2019).
A. N. Guz and V. A. Dekret, “On two models in three-dimensional theory of stability of composite materials,” Int. Appl. Mech., 44, No. 8, 839–854 (2008).
A. N. Guz and V. A. Dekret, “Finite-fiber model in the three-dimensional theory of stability of composites (review),” Int. Appl. Mech., 52, No. 1, 1–48 (2016).
A. N. Guz, V. A. Dekret, Yu. V. Kokhanenko, “Two-dimensional stability problem for two interacting short fiber model in composite: in-line arrangement,” Int. Appl. Mech., 40, No. 9, 994–1001 (2004).
A. N. Guz and Yu. V. Kokhanenko, “Numerical solution of three-dimensional stability problems for elastic body,” Int. Appl. Mech., 37, No. 11, 1369–1399 (2001).
A. N. Guz and Yu. N. Lapusta, “Three-dimensional problems of the near-surface instability of fiber composites in compression (model of piecewise uniform medium) (survey),” Int. Appl. Mech., 35, No. 7, 641–670 (1999).
V. A. Dekret, “Near-surface instability of composite materials weakly reinforced with short fibers,” Int. Appl. Mech., 44, No. 6, 609–625 (2008).
V. A. Dekret, V. S. Zelenskii, and V. M. Bystrov, “Numerical analysis of the stability of a laminated composite with uniaxially compressed reinforcement plies,” Int. Appl. Mech., 50, No. 5, 549–557 (2014).
J. Harich, Y. Lapusta, and W. Wagner, “3D FE-modeling of surface and anisotropy effects during micro-buckling fiber composites,” Compos. Struct., 89, No. 4, 551–555 (2009).
A. N. Khimich, V. A. Dekret, A. V. Popov, and A. V. Chistyakov, “Numerical study of the stability of composite materials on computers of hybrid architecture,” J. Autom. Inform. Sci., 50, No. 7, 7–24 (2018).
A. N. Khimich, A. V. Popov, and O. V. Chistyakov, “Hybrid algorithms for solving the algebraic eigenvalue problem with sparse matrix,” Ñóber. and Syst. Analysis, 53, No. 6, 132–146 (2017).
Author information
Authors and Affiliations
Corresponding author
Additional information
The studies were sponsored by the budget program “Support for Priority Areas of Scientific Research” and “Mathematical modeling of complex interdisciplinary processes and systems on the basis of intelligent supercomputer, grid and cloud technologies” (KPKVK 6541230).
Translated from Prykladna Mekhanika, Vol. 57, No. 6, pp. 81–95, November–December 2021.
Rights and permissions
About this article
Cite this article
Dekret, V.A., Bystrov, V.M. & Zelenskyi, V.S. Numerical Analysis of the Buckling of Near-Surface Short Fibers in a Weakly Reinforced Composite Material*. Int Appl Mech 57, 687–699 (2021). https://doi.org/10.1007/s10778-022-01118-5
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10778-022-01118-5