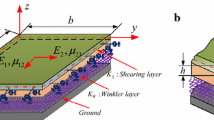
Spatial quasi-static and dynamic problems of the theory of elasticity, simulating the behavior of lithospheric plates and blocks of Earth’s crust are solved for a layered package. According to the data of seismic stations, GPS, inclinometers, and other measuring instruments, slow (age-related) and transient motions of lithospheric plates are considered. It is shown that by carrying out regular measurements, based on the obtained solutions, it is possible to trace the entire process of preparation and occurrence of earthquakes.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
V. A. Babeshko and O. M. Babeshko, “On the study of boundary-value problems of seismology,” Ekol. Vestn. Nauch. Tsentr. ChES, No. 3, 5–10 (2004).
V. A. Babeshko, O. V. Evdokimova, and O. M. Babeshko, “Starting earthquake with harmonic effects in spatial case,” Ekol. Vestn. Nauch. Tsentr. ChES, 15, No. 2, 24–29 (2018).
C. Lomnitz and K. S. Singh, “Earthquakes and Earthquake Prediction,” in: C. Lomnitz and E. Rosenblueth (eds.), Seismic Risk and Engineering Decisions, Elsevier, New York (1976), pp. 3–30.
L. A. Aghalovyan, Asymptotic Theory of Anisotropic Plates and Shells, World Scientific Publishing, Singapore, London (2015).
L. A. Aghalovyan, “On some classes of 3D boundary-value problems of statics and dynamics of plates and shells,” in: Shell and Membrane Theories in Mechanics and Biology, Springer, Switzerland (2015), pp. 1–23.
L. A. Aghalovyan, “On one class of three-dimensional problems of elasticity theory for plates,” Proc. of the A. Razmadze Math. Instit., No. 155, 3–10 (2011).
M. Anderson, Investigating Plate Tectonics, Earthquakes and Volcanoes, Britannica Educational Publishing, New York (2012).
S. Basar, D. Coupland, and H. U. Obrist, The Age of Earthquakes, Penguin Books, London (2015).
B. A. Bolt, Earthquakes, W. H. Freeman and Company, San Francisco (1978).
R. A. Gallant, Plates: Restless Earth, Marshall Cavendish, New York (2003).
B. Gutenberg and C. F. Richter, “Earthquake magnitude, intensity, energy and acceleration,” Bulletin of the Seismological Soc. Amer., 46, No. 2, 105–145 (1956).
K. Kasahara, Earthquake Mechanics, Cambridge University Press, Cambridge (1981).
H. Le Pichon, J. Franchetean, and J. Bonnin, Plate Tectonics, Amsterdam, Elsevier (1973).
T. Rikitake, Earthquake Prediction, Elsevier, Amsterdam (1976).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Prikladnaya Mekhanika, Vol. 57, No. 1, pp. 29–43, January–February 2021.
Rights and permissions
About this article
Cite this article
Ahalovian, L.A., Ahalovian, M.L. One Class of Problems of the Theory of Elasticity and Seismology and a Problem of Earthquake Prediction. Int Appl Mech 57, 19–33 (2021). https://doi.org/10.1007/s10778-021-01063-9
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10778-021-01063-9