Skip to main content
SpringerLink
Log in

Stochastic stability of three-dimensional linear systems under parametric random action

  • Published:
International Applied Mechanics Aims and scope

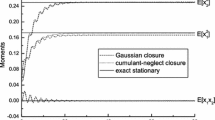
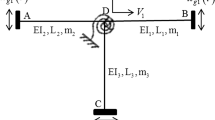
The stability of a three-dimensional linear system, driven by a parametric random excitation is considered. The stability of the system is investigated using a combination of stochastic averaging method and a probabilistic approach. For this purpose, it is necessary to find the transient probability density of the components of the vector random process. Thus, the invariant measure of the system may be calculated from the stationary solutions of the associated Fokker–Planck equations. These solutions are obtained numerically, using the sweep method. As a comparison criterion, a digital simulation of Itô equations has been carried out using the Monte-Carlo simulation (MCS) method. As an application, the example of instability of a thin-walled bar under the effect of parametric random action is considered

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. S. T. Ariaratnam and Wei-Chau Xie, “Lyapunov exponents and stochastic stability of two-dimensional parametrically excited random systems,” Trans. ASME, Ser. E. J. Appl. Mech., 60, No. 3, 667–682 (1993).

    MathSciNet  ADS  Google Scholar 

  2. E. I. Auslender and G. N. Mil’stein, “Asymptotic expansions of the Lyapunov index for linear stochastic systems with small noise,” J. Appi. Math. Mech., 46, 277–283 (1983).

    Article  Google Scholar 

  3. R. Bellman, Stability Theory of Differential Equations, Dover, New York (1969).

    Google Scholar 

  4. V. V. Bolotin, Dynamic Stability of Elastic Systems [in Russian], Gostekhizdat, Moscow (1956).

    Google Scholar 

  5. V. V. Bolotin, Vibrations in Engineering: Handbook [in Russian], Nauka, Mashinostroenie, Moscow (1978).

    Google Scholar 

  6. M. F. Dimentberg, Stochastic Processes in Dynamic Systems with Variable Parameters [in Russian], Nauka, Moscow (1989).

    Google Scholar 

  7. R. Z. Khasminskii, Stability of System of Differential Equations in Random Perturbations of Their Parameters [in Russian], Nauka, Moscow (1969).

    Google Scholar 

  8. H. J. Kushner, Stochastic Stability and Control, Academic Press, New York (1967), pp. 114–127.

    MATH  Google Scholar 

  9. J. Salle, S. La, and S. Lefschetz, Stability by Lyapunov’s Direct Method with Applications, Academic Press, New York (1961), pp. 324–329.

    Google Scholar 

  10. M. Labou, “Stochastic stability of parametrically excited random systems,” Int. Appl. Mech., 40, No. 10, 1175–1183 (2004).

    MathSciNet  Google Scholar 

  11. M. Labou and D. Ma, “Lyapunov exponents of coupled two-DOF stochastic linear systems and related stability problems,” J. Sound Vib., 325, 421–435 (2008).

    Article  ADS  Google Scholar 

  12. K. M. Liew and X. Liu, “The maximum Lyapunov exponent for a three-dimensional stochastic system,” J. Appl. Mech., 71, 677–690 (2004).

    Article  MATH  MathSciNet  Google Scholar 

  13. X. B. Liu and K. M. Liew, “The Lyapunov exponent for a co-dimension two bifurcation system driven by a real noise,” Int. J. Non-Linear Mech., 38, 1495–1511 (2003).

    Article  MATH  MathSciNet  ADS  Google Scholar 

  14. X. B. Liu and K. M. Liew, “On the almost-sure stability condition for a co-dimensional two bifurcation system under the parametric excitation of a real noise,” J. Sound Vibr., 272, 85–107 (2004).

    Article  MathSciNet  ADS  Google Scholar 

  15. R. R. Mitchell and F. Kozin, “Sample stability of second-order linear differential equations with wide-band noise coefficients,” SIAM J. Appl. Math., 27, No. 4, 571–604 (1974).

    Article  MATH  MathSciNet  Google Scholar 

  16. N. S. Namachchivaya and H. J. Van Roessel, “Maximal Lyapunov exponent and rotation numbers for two coupled oscillators driven by real noise,” J. Stat. Phys., 71, 549–567 (1993).

    Article  MATH  ADS  Google Scholar 

  17. N. S. Namachchivaya and S. Taiwar, “Maximal Lyapunov exponents and rotation numbers for stochastically perturbed co-dimension two bifurcation,” J. Sound Vibr., 169, 349–372 (1993).

    Article  Google Scholar 

  18. A. A. Samarskii and A. V. Gulin, Numerical Methods [in Russian], Nauka, Moscow (1989).

    MATH  Google Scholar 

  19. T. T. Soog and M. Grigoriu, Random Vibration of Mechanical and Structural Systems, Prentice Hall, New Jersey (1992), pp. 415–425.

    Google Scholar 

  20. R. L. Stratonovich and Yu. M. Romanovskii, “Parametric effect of a random force on linear and non-linear oscillatory systems,” in: P. I. Kuznetsov, R. L. Stratonovich, and V. Tikhonov (eds.), Non-Linear Transformation of Stochastic Processes, Pergamon Press, Oxford (1965).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. University of Hawaii at Manoa, 2540 Dole Street, Honolulu, HI, 96822, USA

    M. Labou

Authors
  1. M. Labou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Labou.

Additional information

Published in Prikladnaya Mekhanika, Vol. 46, No. 4, pp. 124–143, April 2010.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Labou, M. Stochastic stability of three-dimensional linear systems under parametric random action. Int Appl Mech 46, 474–490 (2010). https://doi.org/10.1007/s10778-010-0331-3

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10778-010-0331-3

Keywords

Search

Navigation