Abstract
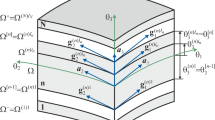
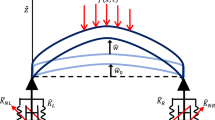
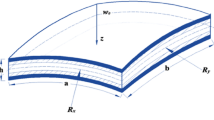
Nonlinear vibrations of viscoelastic orthotropic and isotropic shells are mathematically modeled using a geometrically nonlinear Timoshenko theory. Nonlinear problems are solved by using the Bubnov-Galerkin method and a numerical method based on quadrature formulas. Results obtained from different theories are compared and analyzed. For each problem, the Bubnov-Galerkin method is tested for convergence. The influence of the viscoelasticity and inhomogeneity of materials on the vibrations of plates is demonstrated
Similar content being viewed by others
References
S. A. Ambartsumyan, Theory of Anisotropic Plates [in Russian], Nauka, Moscow (1987).
F. B. Badalov and Kh. Éshmatov, “Investigation of nonlinear vibrations of viscoelastic plates with initial imperfections,” Int. Appl. Mech., 26, No. 8, 799–804 (1990).
F. B. Badalov, Kh. Éshmatov, and U. I. Akbarov, “Stability of a viscoelastic plate under dynamic loading,” Int. Appl. Mech., 27, No. 9, 892–899 (1991).
F. B. Badalov, Kh. Éshmatov, and M. Yusupov, “Some methods of solving systems of integro-differential equations in viscoelastic problems,” Prikl. Mat. Mekh., 51, No. 5, 867–871 (1987).
A. E. Bogdanovich, Nonlinear Dynamic Problems for Cylindrical Composite Shells [in Russian], Zinatne, Riga (1987).
A. S. Vol’mir, Nonlinear Dynamics of Plates and Shells [in Russian], Nauka, Moscow (1972).
A. Ya. Grigorenko, “Numerical solution of the nonlinear free vibrations of a plate,” Int. Appl. Mech., 19, No. 10, 902–905 (1983).
A. Ya. Grigorenko, “Spline-collocation analysis of the natural vibrations of rectangular plates with varying thickness,” Prikl. Mekh., 26, No. 12, 116–118 (1990).
A. A. Il’yushin and B. E. Pobedrya, Fundamentals of the Mathematical Theory of Thermoviscoelasticity [in Russian], Nauka, Moscow (1970).
Ya. F. Kayuk, Nonlinear Problems in the Theory of Plates and Shells [in Russian], Naukova Dumka, Kiev (1987).
Ya. F. Kayuk and V. K. Khizhnyak, “Nonlinear vibrations of a rectangular plate excited by a moving load,” Prikl. Mekh., 26, No. 6, 122–125 (1990).
M. A. Koltunov, Creep and Relaxation [in Russian], Vysshaya Shkola, Moscow (1976).
P. Z. Lugovoi and V. P. Mukoid, “Nonsteady deformation of a cylindrical shell with a hole under a transient load,” Int. Appl. Mech., 29, No. 9, 752–759 (1993).
S. P. Timoshenko and S. Woinowsky-Krieger, Theory of Plates and Shells, McGraw-Hill, New York (1959).
Kh. Éshmatov, Integral Method for Mathematical Simulation of Dynamic Problems for Viscoelastic Systems [in Russian], Author’s Abstract of D.Sci. Thesis, Kiev (1991).
B. Kh. Éshmatov, “Mathematical simulation of nonlinear vibrations and dynamic stability of viscoelastic orthotropic plates with initial imperfections,” in: Abstracts 5th All-Russian Conf. of Young Scientists on Mathematical Simulation and Information Technologies [in Russian], Novosibirsk, November 1–3 (2004), pp. 34–35.
B. Kh. Éshmatov, “Nonlinear vibrations of viscoelastic orthotropic cylindrical shells in which elastic waves propagate,” in: Proc. 17th Session Int. School on Models of Continuum Mechanics [in Russian], Kazan, July 4–10 (2004), pp. 186–191.
B. Kh. Éshmatov, “Mathematical model of the nonlinear vibrations and dynamic stability of viscoelastic orthotropic shells with shear strains and rotary inertia,” Dokl. AN RUz, No. 1, 13–16 (2005).
Z. Bao, S. Mukherjee, M. Roman, and N. Aubry, “Nonlinear vibrations of beams, strings, plates, and membranes without initial tension,” ASME, J. Appl. Mech., 71, 551–559 (2004).
W. Han and M. Petyt, “Geometrically nonlinear vibration analysis of thin, rectangular plates using the hierarchical finite element method-I: The fundamental mode of isotropic plates,” Computers & Structures, 63, No. 2, 295–308 (1997).
B. A. Khudayarov, “Numerical analysis of the nonlinear flutter of viscoelastic plates,” Int. Appl. Mech., 41, No. 5, 538–543 (2005).
V. I. Kozlov and T. V. Karnaukhova, “Basic equations for viscoelastic laminated shells with distributed piezoelectric inclusions intended to control nonstationary vibrations,” Int. Appl. Mech., 38, No. 10, 1253–1260 (2002).
V. D. Kubenko and P. S. Koval’chuk, “Influence of initial geometric imperfections on the vibrations and dynamic stability of elastic shells,” Int. Appl. Mech., 40, No. 8, 847–877 (2004).
P. Z. Lugovoi, V. F. Meish, and S. E. Shtantsel’, “Forced nonstationary vibrations of a sandwich cylindrical shell with cross-ribbed core,” Int. Appl. Mech., 41, No. 2, 161–167 (2005).
V. F. Meish and A. S. Kairov, “Vibrations of reinforced cylindrical shells with initial deflections under nonstationary loads,” Int. Appl. Mech., 41, No. 1, 42–48 (2005).
V. F. Meish, “Numerical solution of dynamic problems for reinforced ellipsoidal shells under nonstationary loads,” Int. Appl. Mech., 41, No. 4, 386–391 (2005).
Y. X. Sun and S. Y. Zhang, “Chaotic dynamic analysis of viscoelastic plates,” Int. J. Mech. Sci., 43, 1195–1208 (2001).
D. Touati and G. Cederbaum, “Dynamic stability of nonlinear viscoelastic plates,” Int. J. Solids Struct., 31, No. 17, 67–76 (1994).
X. Wang, “Numerical analysis of moving orthotropic thin plates,” Computers & Structures, 70, 467–486 (1999).
Author information
Authors and Affiliations
Additional information
__________
Translated from Prikladnaya Mekhanika, Vol. 42, No. 5, pp. 120–131, May 2006.
Rights and permissions
About this article
Cite this article
Éshmatov, B.K. Nonlinear vibration analysis of viscoelastic plates based on a refined Timoshenko theory. Int Appl Mech 42, 596–605 (2006). https://doi.org/10.1007/s10778-006-0127-7
Received:
Issue Date:
DOI: https://doi.org/10.1007/s10778-006-0127-7