Skip to main content
SpringerLink
Log in

Geodesic Stability for Kehagias-Sfetsos Black Hole in Hořava-Lifshitz Gravity via Lyapunov Exponents

  • Published:
International Journal of Theoretical Physics Aims and scope Submit manuscript

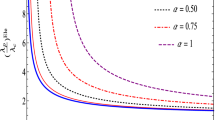
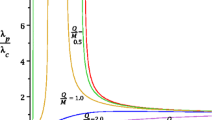
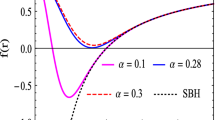
Abstract

By computing the Lyapunov exponent, which is the inverse of the instability time scale associated with this geodesic motion we show that for a general Kehagias-Sfetsos (KS) solution, there is two region of space which in both of them the equatorial timelike geodesics are stable via Lyapunov measure of stability.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Wilkinson, M.: Lyapunov exponent for small particles in smooth one-dimensional flows. arXiv:0911.2917v1

  2. Vanneste, J.: Estimating generalised Lyapunov exponents for products of random matrices. arXiv:0911.2161v2

  3. Roemer, R.A., Baldes, H.S.: The random phase property and the Lyapunov spectrum for disordered multi-channel systems. arXiv:0910.5808v1

  4. Biswas, P., Shimoyama, H., Mead, L.R.: Lyapunov exponent and natural invariant density determination of chaotic maps: an iterative maximum entropy ansatz. arXiv:0910.4561v1

  5. Young, L.-S.: Dimension, entropy, and Lyapunov exponents. Erg. Theory Dyn. Syst. 2, 109–124 (1982)

    Article  MATH  Google Scholar 

  6. Young, L.: Entropy, Lyapunov exponents, and Hausdorff dimension in differentiable dynamic systems. IEEE Trans. Circuit Syst. 8, 599–607 (1983)

    Article  Google Scholar 

  7. Zeeman, E.C.: Bifurcation and catastrophe theory. In: Lidl, R. (ed.) Papers in Algebra, Analysis, and Statistics, pp. 207–272. American Mathematical Society, Providence (1982)

    Chapter  Google Scholar 

  8. Tabor, M.: Chaos and Integrability in Nonlinear Dynamics. Wiley, New York (1989)

    MATH  Google Scholar 

  9. Spirig, F.: Sequence of bifurcations in a three-dimensional system near a critical point. J. Appl. Math. Phys. (ZAMP) 34, 259–276 (1983)

    Article  MATH  MathSciNet  Google Scholar 

  10. Stavans, J., Heslot, F., Libchaber, A.: Fixed winding number and the quasiperiodic route to chaos in a convective fluid. Phys. Rev. Lett. 55, 596–599 (1985)

    Article  ADS  Google Scholar 

  11. Sommerer, J.C., Ditto, W.L., Grebogi, C., Ott, E., Spano, M.L.: Experimental confirmation of the theory for critical exponents of crises. Phys. Lett. A 153, 105–109 (1991)

    Article  ADS  Google Scholar 

  12. Goldhirsch, I., Sulem, P.L., Orszag, S.: Physica D 27, 311 (1987)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  13. Lyapunov, A.M.: The General Problem of the Stability of Motion. Taylor and Francis, London (1992). ISBN 978-0748400621

    MATH  Google Scholar 

  14. Cardoso, V., Miranda, A.S., Berti, E., Witek, H., Zanchin, V.T.: Phys. Rev. D 79, 064016 (2009)

    Article  MathSciNet  ADS  Google Scholar 

  15. Arnbwitt, R., Deser, S., Misner, C.W.: Republication of: The dynamics of general relativity. Gen. Relativ. Gravit. 40, 1997 (2008)

    Article  ADS  Google Scholar 

  16. Hořava, P.: J. High Energy Phys. 03, 020 (2009)

    ADS  Google Scholar 

  17. Hořava, P.: Phys. Rev. D 79, 084008 (2009). arXiv:0901.3775v2 [hep-th]

    Article  MathSciNet  ADS  Google Scholar 

  18. Hořava, P.: Phys. Rev. Lett. 102, 161301 (2009). arXiv:0902.3657v2 [hep-th]

    Article  MathSciNet  ADS  Google Scholar 

  19. Kiritsis, E., Kofinas, G.: Nucl. Phys. B 821, 467 (2009). arXiv:0904.1334v4 [hep-th]

    Article  MathSciNet  ADS  MATH  Google Scholar 

  20. Kehagias, A., Sfetsos, K.: Phys. Lett. B 678, 123 (2009). arXiv:0905.0477v1 [hep-th]

    Article  MathSciNet  ADS  Google Scholar 

  21. Wang, M., Jing, J., Ding, C., Chen, S.: First laws of thermodynamics in IR modified Hořava-Lifshitz gravity. arXiv:0912.4832v2 [gr-qc]

  22. Reissner, H.: Uber die Eigengravitation des elektrischen Feldes nach der Einsteinschen Theorie. Ann. Phys. (Germany) 50, 106 (1916)

    Article  ADS  Google Scholar 

  23. Chandrasekhar, S.: The Mathematical Theory of Black Holes. Oxford University Press, New York (1983)

    MATH  Google Scholar 

  24. Konoplya, R.A.: Phys. Lett. B 679, 499 (2009)

    Article  MathSciNet  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Science of Bijar, University of Kurdistan, Bijar, Iran

    M. R. Setare

  2. Physics Department, Faculty of Science, Tarbiat Moalem University, Tehran, Iran

    D. Momeni

Authors
  1. M. R. Setare
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. D. Momeni
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to D. Momeni.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Setare, M.R., Momeni, D. Geodesic Stability for Kehagias-Sfetsos Black Hole in Hořava-Lifshitz Gravity via Lyapunov Exponents. Int J Theor Phys 50, 106–113 (2011). https://doi.org/10.1007/s10773-010-0498-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10773-010-0498-8

Keywords

Search

Navigation