Skip to main content

Advertisement

SpringerLink
Log in

A Self-Regulation Model of Mathematics Achievement for Eleventh-Grade Students

  • Published:
International Journal of Science and Mathematics Education Aims and scope Submit manuscript

Abstract

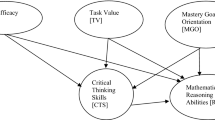
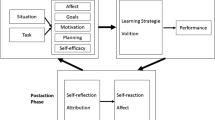
In recent years, mathematical thinking and reasoning have been widely discussed to promote students’ abilities to apply mathematical knowledge and ideas in their daily living. However, few studies have investigated the role of self-regulation in relation to reasoning. This study examined the effects of self-regulation processes on student mathematical reasoning and academic achievement. Using a quantitative research design and the PLS-SEM technique, data were collected from 248 private school students in Malaysia. The PLS-SEM results showed that behavioral regulations, including processes of self-observation, self-judgment, and self-reaction, are decisive factors in influencing student academic achievement and student mathematical reasoning ability. The dimensions of motivational regulation, including processes of self-efficacy, task value, and mastery goal orientation, are dominant factors influencing student reasoning ability, followed by cognition regulation, which includes use of elaboration strategy and critical thinking skills. The study also found that cognition regulation is a significant mediator of the relationship between motivational regulation and reasoning ability. Behavioral and cognition regulation processes, as well as students’ reasoning ability, are the mediators of motivational regulation on academic achievement. The results of this study suggest that teachers should foster the adoption of self-regulation processes in mathematics learning.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  • Artino, A. R. (2005). Review of the motivated strategies for learning questionnaire. Retrieved August 23, 2017, from http://files.eric.ed.gov/fulltext/ED499083.pdf.

  • Azar, H. K., Lavasani, M. G., Malahmadi, E., & Amani, J. (2010). The role of self-efficacy, task value, and achievement goals in predicting learning approaches and mathematics achievement. Procedia - Social and Behavioral Sciences, 5(2), 942–947. https://doi.org/10.1016/j.sbspro.2010.07.214.

    Article  Google Scholar 

  • Bayat, S., & Tarmizi, R. A. (2010). Assessing cognitive and metacognitive strategies during algebra problem solving among university students. Procedia - Social and Behavioral Sciences, 8, 403–410. https://doi.org/10.1016/j.sbspro.2010.12.056.

    Article  Google Scholar 

  • Borich, G. D., & Tombari, M. L. (1996). Cognitive learning I: Understanding effective thinking. In Second edition Educational psychology: a contemporary approach. Harpercollins College Div. Retrieved March 20, 2017, from http://ows.edb.utexas.edu/sites/default/files/users/borichgd/book/chapter5.pdf.

  • Brodie, K. (Ed.). (2010). Teaching mathematical reasoning in secondary school classrooms. New York: Springer US. https://doi.org/10.1007/978-0-387-09742-8.

  • Danisman, S., & Erginer, E. (2017). The predictive power of fifth graders’ learning styles on their mathematical reasoning and spatial ability. Cogent Education, 4(1), 1–18. https://doi.org/10.1080/2331186X.2016.1266830.

    Article  Google Scholar 

  • Davadas, S. D., & Lay, Y. F. (2018). Factors affecting students’ attitude toward mathematics: A structural equation modeling approach. Eurasia Journal of Mathematics, Science and Technology Education, 14(1), 517–529. https://doi.org/10.12973/ejmste/80356.

  • Dent, A. L., & Koenka, A. C. (2016). The relation between self-regulated learning and academic achievement across childhood and adolescence: A meta-analysis. Educational Psychology Review, 28(3), 425–474. https://doi.org/10.1007/s10648-015-9320-8.

  • Duarte, P., & Amaro, S. (2018). Methods for modelling reflective-formative second order constructs in PLS: An application to online travel shopping. Journal of Hospitality and Tourism Technology. https://doi.org/10.1108/JHTT-09-2017-0092.

  • Fadlelmula, F. K., Cakiroglu, E., & Sungur, S. (2015). Developing a structural model on the relationship among motivational beliefs, self-regulated learning strategies, and achievement in mathematics. International Journal of Science and Mathematics Education, 13(6), 1355–1375. https://doi.org/10.1007/s10763-013-9499-4.

    Article  Google Scholar 

  • Hair, J. F., Hult, G. T. M., Ringle, C. M., & Sarstedt, M. (2014). A primer on partial least squares structural equation modeling (PLS-SEM). Thousand Oaks, CA: Sage.

    Google Scholar 

  • Hair, J. F., Hult, G. T. M., Ringle, C. M., & Sarstedt, M. (2017). A primer on partial least squares structural equation modeling (PLS-SEM) (2nd ed.). Thousand Oaks, CA: Sage.

    Google Scholar 

  • Iskender, M. (2009). The relationship between self-compassion, self-efficacy, and control belief about learning in Turkish university students. Social Behavior and Personality, 37(5), 711–720. https://doi.org/10.2224/sbp.2009.37.5.711.

    Article  Google Scholar 

  • Keskin, H. K. (2014). A path analysis of metacognitive strategies in reading, self-efficacy, and task value. International Journal of Social Sciences and Education, 4(4), 2223–4934. Retrieved December 25, 2017, from https://www.researchgate.net/publication/290908854_A_Path_Analysis_of_Metacognitive_Strategies_in_Reading_Self-Efficacy_and_Task_Value.

  • Lan, W. Y. (1996). The effects of self-monitoring on students’ course performance, use of learning strategies, attitude, self-judgment ability, and knowledge representation. The Journal of Experimental Education, 64(2), 101–115.

    Article  Google Scholar 

  • Latan, H. (2018). PLS path modeling in hospitality and tourism research: the golden age and days of future past. In F. Ali, S. M. Rasoolimanesh, & C. Cobanoglu (Eds.), Applying partial least squares in tourism and hospitality research (1st ed., pp. 1–35). Bingley, England: Emerald Publishing Limited. https://doi.org/10.1108/978-1-78756-699-620181004.

  • Li, M., Zheng, C., Liang, J. C., Zhang, Y., & Tsai, C. C. (2018). Conceptions, self-regulation, and strategies of learning science among Chinese high school students. International Journal of Science and Mathematics Education, 16(1), 69–87. https://doi.org/10.1007/s10763-016-9766-2.

  • Mason, L., Boscolo, P., Tornatora, M. C., & Ronconi, L. (2013). Besides knowledge: a cross-sectional study on the relations between epistemic beliefs, achievement goals, self-beliefs, and achievement in science. Instructional Science, 41(1), 49–79. https://doi.org/10.1007/s11251-012-9210-0.

    Article  Google Scholar 

  • Mayer, R. E. (1998). Cognitive, metacognitive, and motivational aspects of problem solving. Instructional Science, 26(1), 49–63. https://doi.org/10.1023/A:1003088013286.

    Article  Google Scholar 

  • Monecke, A., & Leisch, F. (2012). semPLS: Structural equation modeling using partial least squares. Journal of Statistical Software, 48(3), 1–32. https://doi.org/10.18637/jss.v048.i03.

    Article  Google Scholar 

  • Mousoulides, N., & Philippou, G. (2005). Students’ motivational beliefs, self-regulation strategies and mathematics achievement. In H. L. Chick & J. L. Vincent (Eds.), Proceedings of the 29th Conference of the International Group for the Psychology of Mathematics Education 3, 321–328. Melbourne: PME.

  • National Center for Education Statistics. (n.d.). NAEP questions tool. Retrieved January 7, 2018, from https://nces.ed.gov/NationsReportCard/nqt/.

  • National Council of Teachers of Mathematics. (2009). Focus in high school mathematics: Reasoning and sense making. Reston: Author.

  • NCTM Research Committee. (2011). Trends and issues in high school mathematics: Research insights and needs. Journal for Research in Mathematics Education, 42(3), 204–219.

    Article  Google Scholar 

  • Ng, B. L. L., Liu, W. C., & Wang, J. C. K. (2016). Student motivation and learning in mathematics and science: A cluster analysis. International Journal of Science and Mathematics Education, 14(7), 1359–1376. https://doi.org/10.1007/s10763-015-9654-1.

  • Panadero, E., & Alonso-tapia, J. (2014). How do students self-regulate? Review of Zimmerman’s cyclical model of self-regulated learning. Annals of Psychology, 30(2), 450–462. https://doi.org/10.6018/analesps.30.2.167221.

    Article  Google Scholar 

  • Parvin, K., Vahid, M. T., & Gholamreza, S. (1998). Relationship between self-regulated learning strategies with academic achievement: A meta-analysis. Education and Educational Technologies, 78–80.

  • Pintrich, P. R. (2004). A conceptual framework for assessing motivation and self-regulated learning in college students. Educational Psychology Review, 16(4), 385–407.

    Article  Google Scholar 

  • Pintrich, P. R., & de Groot, E. V. (1990). Motivational and self-regulated learning components of classroom academic performance. Journal of Educational Psychology, 82(1), 33–40. https://doi.org/10.1037/0022-0663.82.1.33.

    Article  Google Scholar 

  • Podsakoff, P. M., MacKenzie, S. B., Lee, J. Y., & Podsakoff, N. P. (2003). Common method biases in behavioral research: A critical review of the literature and recommended remedies. Journal of Applied Psychology, 88(5), 879–903. https://doi.org/10.1037/0021-9010.88.5.879.

  • Ramdass, D., & Zimmerman, B. J. (2008). Effects of self-correction strategy training on middle school students’ self-efficacy, self-evaluation, and mathematics division learning. Journal of Advanced Academics, 20(1), 18–41.

    Article  Google Scholar 

  • Rashid, R. A., & Hashim, R. A. (2008). The relationship between critical thinking and language proficiency of Malaysian undergraduates. In EDU-COM International Conference (pp. 19–21). Retrieved December 25, 2017, from http://ro.ecu.edu.au/cgi/viewcontent.cgi?article=1035&context=ceducom

  • Ringle, C. M., Wende, S., & Becker, J.-M. (2015). SmartPLS 3. Boenningstedt, Germany: SmartPLS GmbH. Retrieved September 27, 2018, from http://www.smartpls.com.

  • Schoenfeld, A. H. (2016). Research in mathematics education. Review of Research in Education, 40(1), 497–528. https://doi.org/10.3102/0091732X16658650.

    Article  Google Scholar 

  • Tee, K. N., Leong, K. E., & Abdul Rahim, S. S. (2018) The mediating effects of critical thinking skills on motivation factors for mathematical reasoning ability. The Asia-Pacific Education Researcher, 27(5), 373–382. https://doi.org/10.1007/s40299-018-0396-z

  • Velayutham, S., & Aldridge, J. M. (2013). Influence of psychosocial classroom environment on students’ motivation and self-regulation in science learning: A structural equation modeling approach. Research in Science Education, 43(2), 507–527. https://doi.org/10.1007/s11165-011-9273-y.

  • Verawati, Arifin, S. R., Idris, R., & Hamid, N. A. A. (2010). Gender analysis of MyCT (Malaysian critical thinking) instrument. Procedia - Social and Behavioral Sciences, 7(2), 70–76. https://doi.org/10.1016/j.sbspro.2010.10.011.

    Article  Google Scholar 

  • Vogt, C. M., Hocevar, D., & Hagedorn, L. S. (2007). A social cognitive construct validation: Determining women’s and men’s success in engineering programs. The Journal of Higher Education, 78(3), 337–364.

    Article  Google Scholar 

  • Weinstein, C. E., Husman, J., & Dierking, D. R. (2000). Self-regulation interventions with a focus on learning strategies. In M. Boekaerts, P. R. Pintrich, & M. Zeidner (Eds.), Handbook of self-regulation (pp. 727–747). San Diego, CA: Academic Press. https://doi.org/10.1016/B978-012109890-2/50051-2.

    Chapter  Google Scholar 

  • Wilson, J. E., & Weinstein, C. E. (1989). Identifying and evaluating potential instructional components for high school learning strategies programs. The High School Journal, 72(3), 136–142.

    Google Scholar 

  • Wu, P. H. (2005). Examining the effects of self-regulated learning on junior high school students’ academic performance using structural equation modeling. National Taiwan University of Science and Technology. Retrieved August 23, 2017, from http://ir.csu.edu.tw/bitstream/987654321/603/1/20100520021.pdf.

  • Yang, K.-L. (2012). Structures of cognitive and metacognitive reading strategy use for reading comprehension of geometry proof. Educational Studies in Mathematics, 80(3), 307–326. https://doi.org/10.1007/s10649-011-9350-1.

    Article  Google Scholar 

  • Zimmerman, B. J. (1989). A social cognitive view of self-regulated academic learning. Journal of Educational Psychology, 81(3), 329–339.

    Article  Google Scholar 

  • Zimmerman, B. J. (2002). Becoming a self-regulated learner: An overview. Theory Into Practice, 41(2), 64–70. https://doi.org/10.1207/s15430421tip4102_2.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics and Science Education, Faculty of Education, University of Malaya, 50603, Kuala Lumpur, Malaysia

    Kiew Nee Tee, Kwan Eu Leong & Suzieleez Syrene Abdul Rahim

Authors
  1. Kiew Nee Tee
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kwan Eu Leong
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Suzieleez Syrene Abdul Rahim
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kiew Nee Tee.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tee, K.N., Leong, K.E. & Abdul Rahim, S.S. A Self-Regulation Model of Mathematics Achievement for Eleventh-Grade Students. Int J of Sci and Math Educ 19, 619–637 (2021). https://doi.org/10.1007/s10763-020-10076-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10763-020-10076-8

Keywords

Search

Navigation