Skip to main content

Advertisement

SpringerLink
Log in

Modeling Chilean Mathematics Teachers’ Instructional Beliefs on Problem Solving Practices

  • Published:
International Journal of Science and Mathematics Education Aims and scope Submit manuscript

Abstract

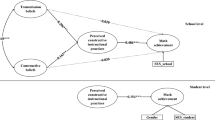
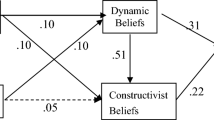
This study was designed to examine predictors of instructional beliefs related to problem solving that influence mathematics in-service teachers’ practices in the Chilean context. A total of 713 in-service mathematics teachers from various elementary schools participated in the survey study during 2015 and 2016. Results showed that teachers’ traditional beliefs are directly associated with their teacher-centered practices, while there was an indirect relation among reformed beliefs and student-centered practices through teachers’ self-efficacy beliefs and their beliefs about the value of problem solving. This association among beliefs and practices suggests that educators and policy makers should be aware of, when designing a teacher professional development, the need to emphasize other variables such as teachers’ self-efficacy and value of the task.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  • Ávalos, B., & De Los Rios, D. (2013). Reform environment and teacher identity in Chile. In D. B. Napier & S. Majhanovich (Eds.), Education, dominance and identity (pp. 153–175). Rotterdam: Sense.

    Chapter  Google Scholar 

  • Ávalos, B., & Matus, C. (2010). La formación inicial docente en Chile desde una óptica internacional. Informe nacional del Estudio Internacional IEA TEDS-M [Initial training in Chile from an international perspective. National Report of International Study of IEA TEDS-M]. Santiago: Ministerio de Educación.

  • Ávalos, B., & Valenzuela, J. P. (2016). Education for all and attrition/retention of new teachers: A trajectory study in Chile. International Journal of Educational Development, 49, 279–290.

    Article  Google Scholar 

  • Ayarza, R. O., Soto, D. S., & Crocci, H. S. (2007). Renovación de la enseñanza del álgebra elemental: Un aporte desde la didáctica [Renewing the teaching of elementary algebra: A contribution of didactics]. Estudios Pedagógicos (Valdivia), 33(2), 81–100.

  • Bandalos, D. L. (2002). The effects of item parceling on goodness-of-fit and parameter estimate bias in structural equation modeling. Structural Equation Modeling, 9(1), 78–102.

    Article  Google Scholar 

  • Bandura, A. (1997). Self-efficacy: The exercise of control. New York: W H. Freeman.

    Google Scholar 

  • Bellei, C., & Morawietz, L. (2016). Strong content, weak tools twenty-first-century competencies in the Chilean educational reform. In F. M. Reimers & C. Chung (Eds.), Teaching and learning for the twenty-first century: Educational goals, policies, and curricula from six nations (pp. 93–125). Cambridge: Harvard Education Press.

    Google Scholar 

  • Bellei, C., & Vanni, X. (2015). Chile: The evolution of educational policy, 1980–2014. In S. Shwartzman (Ed.), Education in South America: Education around the world (pp. 179–200). London: Bloomsbury.

    Google Scholar 

  • Bent, G. J., Bakx, A., & Den Brok, P. (2017). Primary education teachers’ self-efficacy beliefs for teaching geography lessons. International Research in Geographical and Environmental Education, 26(2), 150–165.

    Article  Google Scholar 

  • Blömeke, S., & Kaiser, G. (2014). Theoretical framework, study design and main results of TEDS-M. In S. Blömeke, F. Hsieh, G. Kaiser, & W. H. Schmidt (Eds.), International perspectives on teacher knowledge, beliefs and opportunities to learn (pp. 19–48). Dordrecht, The Netherlands: Springer.

  • Bong, M. (2001). Role of self-efficacy and task-value in predicting college students’ course performance and future enrollment intentions. Contemporary Educational Psychology, 26(4), 553–570.

    Article  Google Scholar 

  • Burkhardt, H. (2006). Modelling in mathematics classrooms: Reflections on past developments and the future. ZDM, 38(2), 178–195.

    Article  Google Scholar 

  • Byrne, B. (2010). Structural equation modeling using AMOS: Basic concepts, applications, and programming (2nd ed.). New York: Taylor and Francis Group.

    Google Scholar 

  • Cárcamo, R. A., & Castro, P. J. (2015). Concepciones sobre el Aprendizaje de Estudiantes de Pedagogía de la Universidad de Magallanes y Docentes en Ejercicio en la Educación Básica de la ciudad de Punta Arenas, Chile [Conceptions about learning among pre-service students in University of Magallanes and in-service elementary teachers in Punta Arenas, Chile]. Formación Universitaria, 8(5), 13–24.

    Article  Google Scholar 

  • Carrillo, J. (1998). Exploring relationships between teachers’ conceptions and problem solving modes in mathematics. In E. Pehkonen & G. Törner (Eds.), The state of art in mathematics-related beliefs research. Helsinki, Finland: University of Helsinki.

  • Chen, I. (2009). Behaviorism and developments in instructional design and technology. In P. Rogers, G. Berg, J. Boettcher, C. Howard, L. Justice, & K. Shenck (Eds.), Encyclopedia of distance learning (pp. 153–173). Hershey: Idea Group Incorporated.

    Chapter  Google Scholar 

  • Clarke, D., & Hollingsworth, H. (2002). Elaborating a model of teacher professional growth. Teaching and Teacher Education, 18(8), 947–967.

    Article  Google Scholar 

  • Contreras, S. A. (2009). Creencias curriculares y creencias de actuación curricular de los profesores de ciencias chilenos [Chilean sciences teachers’ beliefs about curriculum and its performance]. Revista Electrónica de Enseñanza de las Ciencias, 8(2), 505–526.

    Google Scholar 

  • Cooney, T. J. (1994). Research and teacher education: In search of common ground. Journal for Research in Mathematics Education, 25(6), 608–636.

    Article  Google Scholar 

  • Eccles, J. S. (2005). Subjective task value and the Eccles et al. model of achievement-related choices. In A. J. Elliot & C. S. Dweck (Eds.), Handbook of competence and motivation (pp. 105–121). New York: Guilford Press.

    Google Scholar 

  • Eccles, J. S., Adler, T. F., Futterman, R., Goff, S. B., Kaczala, C. M., Meece, J., & Midgley, C. (1983). Expectancies, values and academic behaviors. In J. T. Spence (Ed.), Achievement and achievement motives (pp. 75–146). San Francisco: Freeman.

    Google Scholar 

  • Eccles, J. S., & Wigfield, A. (2002). Motivational beliefs, values, and goals. Annual Review of Psychology, 53(1), 109–132. https://doi.org/10.1146/annurev.psych.53.100901.135153.

    Article  Google Scholar 

  • Eccles, J. S., Wigfield, A., & Schiefele, U. (1998). Motivation to succeed. In W. Damon & N. Eisenberg (Eds.), Handbook of child psychology: Social, emotional, and personality development (vol. 3, 5th ed., pp. 1017–1095). Hoboken: Wiley.

    Google Scholar 

  • Evers, W. J., Brouwers, A., & Tomic, W. (2002). Burnout and self-efficacy: A study on teachers’ beliefs when implementing an innovative educational system in the Netherlands. British Journal of Educational Psychology, 72(2), 227–243.

    Article  Google Scholar 

  • Farmer, J. A., Buckmaster, A., & LeGrand, B. (1992). Cognitive apprenticeship: Implications for continuing professional education. New Directions for Adult and Continuing Education, 1992(55), 41–49.

    Article  Google Scholar 

  • Feather, N. T. (1992). Values, valences, expectations, and actions. Journal of Social Issues, 48(2), 109–124.

    Article  Google Scholar 

  • Felbrich, A., Kaiser, G., & Schmotz, C. (2014). The cultural dimension of beliefs: An investigation of future primary teachers’ epistemological beliefs concerning the nature of mathematics in 15 countries. In S. Blömeke, F. Hsieh, G. Kaiser, & W. H. Schmidt (Eds.), International perspectives on teacher knowledge, beliefs and opportunities to learn (pp. 209–230). Dordrecht: Springer.

    Chapter  Google Scholar 

  • Felmer, P., Lewin, R., Martínez, S., Reyes, C., Varas, L., Chandía, E., . . . Ortíz, A. (2014). Primary mathematics standards for pre-service teachers in Chile: A resource book for teachers and educators (Series on Mathematics Education, Vol. 9). Hackensack: World Scientific Printers.

  • Felmer, P., & Perdomo-Díaz, J. (2016). Novice Chilean secondary mathematics teachers as problem solvers. In P. Felmer, E. Pehkonen, & J. Kilpatrick (Eds), Posing and solving mathematical problems (pp. 287–308). Cham: Springer International Publishing.

  • Flake, J. K., Barron, K. E., Hulleman, C., McCoach, B. D., & Welsh, M. E. (2015). Measuring cost: The forgotten component of expectancy-value theory. Contemporary Educational Psychology, 41, 232–244.

    Article  Google Scholar 

  • Fornell, C., & Larcker, D. F. (1981). Evaluating structural equation models with unobservable variables and measurement error. Journal of Marketing Research, 18(1), 39–50.

    Article  Google Scholar 

  • Grootenboer, P., & Marshman, M. (2016). The affective domain, mathematics, and mathematics education. In P. Grootenboer & M. Marshman (Eds.), Mathematics, affect and learning (pp. 13–33). Singapore: Springer.

    Chapter  Google Scholar 

  • Guskey, T. R. (2002). Professional development and teacher change. Teachers and Teaching, 8(3), 381–391.

    Article  Google Scholar 

  • Handal, B. (2003). Teachers’ mathematical beliefs: A review. The Mathematics Educator, 13(2), 47–57.

    Google Scholar 

  • Hooper, D., Coughlan, J., & Mullen, M. (2008). Structural equation modelling: Guidelines for determining model fit. Electronic Journal of Business Research Methods, 6(1), 53–60.

    Google Scholar 

  • Jonassen, D. H. (1997). Instructional design models for well-structured and ill-structured problem-solving learning outcomes. Educational Technology Research and Development, 45(1), 65–94.

    Article  Google Scholar 

  • Kang, M., & Byun, H. P. (2001). A conceptual framework for a web-based knowledge construction support system. Educational Technology, 41(4), 48–53.

    Google Scholar 

  • Keys, C. W., & Bryan, L. A. (2001). Co-constructing inquiry-based science with teachers: Essential research for lasting reform. Journal of Research in Science Teaching, 38(6), 631–645.

    Article  Google Scholar 

  • Kline, R. B. (2010). Principles and practice of structural equation modeling (3rd ed.). New York: Guilford Press.

  • Leroy, N., Bressoux, P., Sarrazin, P., & Trouilloud, D. (2007). Impact of teachers’ implicit theories and perceived pressures on the establishment of an autonomy supportive climate. European Journal of Psychology of Education, 22(4), 529–545.

    Article  Google Scholar 

  • Ministry of Education Republic of Chile. (2012). Bases Curriculares Matemática; Ficha Bases Curriculares 2012. Santiago, Chile: Ministerio de Educación. Retrieved from http://www.curriculumenlineamineduc.cl/605/w3-article-21321.html.

  • National Council of Teachers of Mathematics. (1991). Professional standards for teaching mathematics. Retrieved from http://www.nctm.org/standards/

  • Organisation for Economic Co-operation and Developmen. (2012). Development co-operation report 2012. Paris, France: OECD Publishing. https://doi.org/10.1787/dcr-2012-en.

  • Peters, E. E. (2010). Shifting to a student-centered science classroom: An exploration of teacher and student changes in perceptions and practices. Journal of Science Teacher Education, 21(3), 329–349.

    Article  Google Scholar 

  • Polya, G. (1945). How to solve it (2nd ed., 1957). Princeton: Princeton University Press.

  • Polya, G. (Ed.). (1981). Mathematical discovery: On understanding, learning, and teaching problem solving (Combined ed.). New York: Wiley.

  • Powell-Moman, A. D., & Brown-Schild, V. B. (2011). The influence of a two-year professional development institute on teacher self-efficacy and use of inquiry-based instruction. Science Educator, 20(2), 47–53.

    Google Scholar 

  • Prawat, R. S. (1992). Teachers’ beliefs about teaching and learning: A constructivist perspective. American Journal of Education, 100(3), 354–395.

    Article  Google Scholar 

  • Preiss, D., Larraín, A., & Valenzuela, S. (2011). Discurso y pensamiento en el aula matemática Chilena [Discourse and thought in Chilean math classroom]. Psykhe, 20(2), 131–146.

    Article  Google Scholar 

  • Raymond, A. M. (1997). Inconsistency between a beginning elementary school teacher’s mathematics beliefs and teaching practice. Journal for Research in Mathematics Education, 28(5), 550–576.

    Article  Google Scholar 

  • Ruffinelli, A. (2016). Ley de desarrollo profesional docente en Chile: de la precarización sistemática a los logros, avances y desafíos pendientes para la profesionalización [Law on teacher professional development: From systematic precariousness to the achievements, the advances, and the remaining challenges for professionalization]. Estudios Pedagógicos, 42(4), 261–279.

    Article  Google Scholar 

  • Sass, D. A., & Smith, P. L. (2006). The effects of parceling unidimensional scales on structural parameter estimates in structural equation modeling. Structural Equation Modeling, 13(4), 566–586.

    Article  Google Scholar 

  • Schiefele, U., & Schaffner, E. (2015). Teacher interests, mastery goals, and self-efficacy as predictors of instructional practices and student motivation. Contemporary Educational Psychology, 42, 159–171.

    Article  Google Scholar 

  • Schmeisser, C., Krauss, S., Bruckmaier, G., Ufer, S., & Blum, W. (2013). Transmissive and constructivist beliefs of in-service mathematics teachers and of beginning university students. In Y. Li & J. N. Moschkovich (Eds.), Proficiency and beliefs in learning and teaching mathematics (pp. 51–67). Rotterdam: Sense.

  • Schoenfeld, A. H. (1999). Models of the teaching process. The Journal of Mathematical Behavior, 18(3), 243–261.

    Article  Google Scholar 

  • Stipek, D. J., Givvin, K. B., Salmon, J. M., & MacGyvers, V. L. (2001). Teachers’ beliefs and practices related to mathematics instruction. Teaching and Teacher Education, 17(2), 213–226.

    Article  Google Scholar 

  • Swan, M. (2006). Designing and using research instruments to describe the beliefs and practices of mathematics teachers. Research in Education, 75(1), 58–70.

    Article  Google Scholar 

  • Tang, S. J., & Hsieh, F. J. (2014). The cultural notion of teacher education: Future lower secondary teachers’ beliefs on the nature of mathematics, the learning of mathematics and mathematics achievement. In S. Blömeke, F. Hsieh, G. Kaiser, & W. H. Schmidt (Eds.), International perspectives on teacher knowledge, beliefs and opportunities to learn (pp. 231–253). Dordrecht: Springer.

  • Tatto, M. T., Rodríguez, M., Ingvarson, L., Rowley, G., Maeda, Y., & Byun, S. Y. (2013). Development of the TEDS-M survey questionnaires. In M. T. Tatto (Ed.), Technical report of The Teacher Education and Development Study in Mathematics (TEDS-M) policy, practice, and readiness to teach primary and secondary mathematics in 17 countries (pp. 47–70). Amsterdam: International Association for the Evaluation of Educational Achievement (IEA).

  • Thompson, A. G. (1985). Teachers’ conceptions of mathematics and the teaching of problem solving. In E. A. Silver (Ed.), Teaching and learning mathematical problem solving: Multiple research perspectives (pp. 281–294). Hillsdale: Erlbaum.

  • Thompson, A. G. (1992). Teachers’ beliefs and conceptions: A synthesis of the research. In D. A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 127–146). New York: Macmillan.

  • Törner, G., Schoenfeld, A. H., & Reiss, K. M. (2007). Problem solving around the world: Summing up the state of the art. ZDM, 39(5–6), 353–353.

    Article  Google Scholar 

  • Tschannen-Moran, M., & Hoy, A. W. (2001). Teacher efficacy: Capturing an elusive construct. Teaching and Teacher Education, 17(7), 783–805.

    Article  Google Scholar 

  • Wigfield, A., Tonks, S., & Klauda, S. L. (2009). Expectancy-value theory. In K. R. Wentzel & A. Wigfield (Eds.), Handbook of motivation at school (pp. 55–75). New York: Routledge Taylor & Francis Group.

Download references

Acknowledgments

The authors are thankful to the ARPA team—mentors, teachers, and researchers, specially Dr Lisa Darragh—for their support and interest in this work.

Funding

Funding from FONDEF ID14I20338 and PIA-CONICYT Basal Funds for Centers of Excellence Project FB0003 is gratefully acknowledged. VG thanks the CONICYT-PCHA/Doctorado Nacional/2013 21130684. FS is also grateful to the support of CONICYT/Fondecyt Postdoctoral Project 3170673.

Author information

Authors and Affiliations

  1. Centro de Investigación Avanzada en Educación (CIAE), Universidad de Chile, Santiago, Chile

    Farzaneh Saadati, Gamal Cerda, Cristian Reyes & Patricio Felmer

  2. Departamento es de Metodología de la Investigación e Informática Educativa, Facultad de Educación, Universidad de Concepción, Concepción, Chile

    Gamal Cerda

  3. Instituto de Ciencias de la Educación, Universidad de O’Higgins, Rancagua, Chile

    Valentina Giaconi

  4. Center for Mathematical Modeling (CMM), Universidad de Chile, Santiago, Chile

    Cristian Reyes & Patricio Felmer

Authors
  1. Farzaneh Saadati
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Gamal Cerda
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Valentina Giaconi
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Cristian Reyes
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Patricio Felmer
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Farzaneh Saadati.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Saadati, F., Cerda, G., Giaconi, V. et al. Modeling Chilean Mathematics Teachers’ Instructional Beliefs on Problem Solving Practices. Int J of Sci and Math Educ 17, 1009–1029 (2019). https://doi.org/10.1007/s10763-018-9897-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10763-018-9897-8

Keywords

Search

Navigation