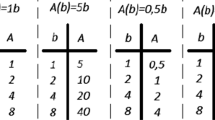
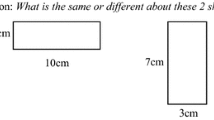
ABSTRACT
The concept of function is a central but difficult topic in secondary school mathematics curricula, which encompasses a transition from an operational to a structural view. The question in this paper is how the use of computer tools may foster this transition. With domain-specific pedagogical knowledge on the learning of function as a point of departure and the notions of emergent modeling and instrumentation as design heuristics, a potentially rich technology-intensive learning arrangement for grade 8 students was designed and field-tested. The results suggest that the relationship between tool use and conceptual development benefits from preliminary activities, from tools offering representations that allow for progressively increasing levels of reasoning, and from intertwinement with paper-and-pencil work.
Article PDF
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
References
Ainley, J., Bills, L. & Wilson, K. E. (2005). Designing spreadsheet-based tasks for purposeful algebra. International Journal of Computers for Mathematical Learning, 10(3), 191–215.
Akkus, R., Hand, B. & Seymour, J. (2008). Understanding students’ understanding of functions. Mathematics Teaching, 207, 10–13.
Artigue, M. (2002). Learning mathematics in a CAS environment: The genesis of a reflection about instrumentation and the dialectics between technical and conceptual work. International Journal of Computers for Mathematical Learning, 7, 245–274.
Bereiter, C. (1985). Towards a solution of the learning paradox. Review of Educational Research, 55(2), 201–226.
Bloch, I. (2003). Teaching functions in a graphic milieu: What forms of knowledge enable students to conjecture and prove? Educational Studies in Mathematics, 52(1), 3–28.
Boon, P. (2008). AlgebraArrows. Retrieved at June 9th, 2008, from http://www.fi.uu.nl/wisweb/en/welcome.html.
Breidenbach, D., Dubinsky, E., Hawks, J. & Nichols, D. (1992). Development of the process conception of function. Educational Studies in Mathematics, 23, 247–285.
Carlson, M., Jacobs, S., Coe, E., Larsen, S. & Hsu, E. (2002). Applying covariational reasoning while modeling dynamic events: A framework and a study. Journal for Research in Mathematics Education, 33, 352–378.
Cobb, P. (2002). Reasoning with tools and inscriptions. The Journal of the Learning Sciences, 11(2&3), 187–215.
Cobb, P. & Yackel, E. (1996). Constructivist, emergent, and sociocultural perspectives in the context of developmental research. Educational Psychologist, 31 (3/4), 175–190.
Doorman, L. M. & Gravemeijer, K. P. E. (2009). Emergent modeling: discrete graphs to support the understanding of change and velocity. ZDM-International Journal on Mathematics Education, 41, 199–211.
Drijvers, P., Doorman, M., Boon, P., Van Gisbergen, S. & Gravemeijer, K. (2007). Tool use in a technology-rich learning arrangement for the concept of function. In Pitta-Pantazi, D., & Philippou, G., Proceedings of CERME 5, 1389–1398.
Dubinsky, E. (1991). Reflective abstraction in advanced mathematical thinking. In D. O. Tall (Ed.), Advanced mathematical thinking (pp. 95–123). Dordrecht: Kluwer.
Duval, R. (2006). A cognitive analysis of problems of comprehension in a learning of mathematics. Educational Studies in Mathematics, 61, 103–131.
Elia, I., Panaoura, A., Eracleous, A. & Gagatsis, A. (2007). Relations between secondary pupils’ conceptions about functions and problem solving in different representations. International Journal of Science and Mathematics Education, 5, 533–556.
Even, R. (1998). Factors involved in linking representations of functions. The Journal of Mathematical Behavior, 17, 105–121.
Falcade, R., Laborde, C. & Mariotti, M. A. (2007). Approaching functions: Cabri tools as instruments of semiotic mediation. Educational Studies in Mathematics, 66, 317–333.
Freudenthal, H. (1983). Didactical phenomenology of mathematical structures. The Netherlands: Reidel: Dordrecht.
Freudenthal, H. (1991). Revisiting mathematics education—China lectures. Dordrecht: Kluwer Academic Publishers.
Gravemeijer, K. (1999). How emergent models may foster the constitution of formal mathematics. Mathematical Thinking and Learning, 1, 155–177.
Gravemeijer, K. (2007). Emergent modelling as a precursor to mathematical modelling. In W. Blum, P. L. Galbraith, H.-W. Henn, & M. Niss (Eds.), Modelling and applications in mathematics education. The 14th ICMI Study (pp 137–144). New York: Springer.
Gravemeijer, K. P. E., Lehrer, R., van Oers, B., & Verschaffel, L. (Eds.). (2002). Symbolizing, modeling and tool use in mathematics education. Dordrecht, the Netherlands: Kluwer Academic Publishers.
Gravemeijer, K., & Cobb, P. (2006). Design research from the learning design perspective. In J. van den Akker, K. Gravemeijer, S. McKenney, & N. Nieveen (Eds.), Educational design research (pp. 17–51). London: Routledge.
Hennessy, S., Ruthven, K. & Brindley, S. (2005). Teacher perspectives on integrating ICT into subject teaching: commitment, constraints, caution and change. Journal of Curriculum Studies, 37(2), 155–192.
Hoyles, C. & Noss, R. (2003). What can digital technologies take from and bring to research in mathematics education? In A. J. Bishop, M. A. Clements, C. Keitel, J. Kilpatrick & F. K. S. Leung (Eds.), Second international handbook of mathematics education (pp. 323–349). Dordrecht: Kluwer Academic Publishers.
Janvier, C. (1987). Translation processes in mathematics education. In C. Janvier (Ed.), Problems of representation in teaching and learning mathematics (pp. 27–32). Hillsdale: Lawrence Erlbaum Associates.
Kalchman, M. & Koedinger, K. (2005). Teaching and learning functions. In S. Donovan & J. Bransford (Eds.), How students learn mathematics (pp. 351–392). Washington DC: National Academy of Sciences.
Kaput, J. & Schorr, R. (2007). Changing representational infrastructures changes most everything: The case of SimCalc, algebra and calculus. In G. W. Blume & M. K. Heid (Eds.), Research on technology and the learning and teaching of mathematics: Vol. 2 cases and perspectives (pp. 211–253). Charlotte: Information Age Publishing.
Kuchemann, D. (1981). Algebra. In K. Hart (Ed.), Children’s understanding of mathematics:11–16 (pp. 102–119). London: Murray.
Lehrer, R. & Schauble, L. (2002). Symbolic communication in mathematics and science: Constituting inscription and thought. In E. D. Amsel & J. Byrnes (Eds.), Language, literacy, and cognitive development. The development and consequences of symbolic communication. (pp. 167–192). Mahwah, NJ: Lawrence Erlbaum Associates.
Malle, G. (2000). Zwei Aspekte von Funktionen: Zuordnung und Kovariation. Mathematik Lehren, 103, 8–11.
Meel, D. (1998). Honors students’ calculus understandings: Comparing Calculus&Mathematica and traditional calculus students. In Shoenfeld, A., J. Kaput, & E. Dubinsky (Eds.) CBMS Issues in Mathematics Education 7: Research in Collegiate Mathematics Education III. pp. 163–215.
Meira, L. (1995). The microevolution of mathematical representations in children’s activity. Cognition and Instruction, 13, 269–313.
Oehrtman, M. C., Carlson, M. P. & Thompson, P. W. (2008). Foundational reasoning abilities that promote coherence in students’ understandings of function. In M. P. Carlson & C. Rasmussen (Eds.), Making the connection: Research and practice in undergraduate mathematics (pp. 27–42). Washington DC: Mathematical Association of America.
Pirie, S. E. B. & Kieren, T. E. (1989). A recursive theory of mathematical understanding. For the Learning of Mathematics, 9(3), 7–11.
Ponce, G. (2007). Critical juncture ahead: Proceed with caution to introduce the concept of function. Mathematics Teacher, 101(2), 136–144.
Ponte, J.P. (1992). The history of the concept of function and some educational implications. The Mathematics Educator, 3(2), 3–8. Retrieved April, 2nd, from http://math.coe.uga.edu/TME/Issues/v03n2/v3n2.html.
Rasmussen, C. & Blumenfeld, H. (2007). Reinventing solutions to systems of linear differential equations: A case of emergent models involving analytic expressions. The Journal of Mathematical Behavior, 26, 195–210.
Sfard, A. (1991). On the dual nature of mathematical conceptions: Reflections on processes and objects as different sides of the same coin. Educational Studies in Mathematics, 22, 1–36.
Sfard, A. & McClain, K. (2002). Special issue: Analyzing tools: Perspective on the role of designed artifacts in mathematics learning. The Journal of the Learning Sciences, 11, 153–388.
Sherin, M. G. (2002). A balancing act: Developing a discourse community in a mathematics community. Journal of Mathematics Teacher Education, 5, 205–233.
Skaja, M. (2003). A secondary school student’s understanding of the concept of function—A case study. Educational Studies in Mathematics, 53(3), 229–254.
Slavit, D. (1997). An alternate route to the reification of function. Educational Studies in Mathematics, 33, 259–281.
Stein, M. K., Engle, R. A., Smith, M. S. & Hughes, E. K. (2008). Orchestrating productive mathematical discussions: Five practices for helping teachers move beyond show and tell. Mathematical Thinking and Learning, 10(4), 313–340.
Tall, D. (1996). Functions and calculus. In A. J. Bishop, K. Clements, C. Keitel, J. Kilpatrick & C. Laborde (Eds.), International handbook on mathematics education (pp. 289–325). Dordrecht: Kluwer Academic Publishers.
Trouche, L. (2004). Managing complexity of human/machine interactions in computerized learning environments: Guiding students’ command process through instrumental orchestrations. International Journal of Computers for Mathematical Learning, 9, 281–307.
van den Heuvel-Panhuizen, M. H. A. M. (2003). The learning paradox and the learning miracle: Thoughts on primary school mathematics education. ZDM-International Journal on Mathematics Education, 24, 96–121.
van Nes, F. T. & Doorman, L. M. (2010). The interaction between multimedia data analysis and theory development in design research. Mathematics Education Research Journal 22(1), 6–30.
Vinner, S. & Dreyfuss, T. (1989). Images and definitions for the concept of function. Journal for Research in Mathematics Education, 20(4), 356–366.
Vygotsky, L. S. (1986). Thought and language—Rev’d edition. Cambridge: A. Kozulin. The MIT Press.
Wertsch, J. V. (1998). Mind as action. New York: Oxford University Press.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Doorman, M., Drijvers, P., Gravemeijer, K. et al. TOOL USE AND THE DEVELOPMENT OF THE FUNCTION CONCEPT: FROM REPEATED CALCULATIONS TO FUNCTIONAL THINKING. Int J of Sci and Math Educ 10, 1243–1267 (2012). https://doi.org/10.1007/s10763-012-9329-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10763-012-9329-0