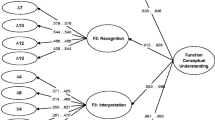
Abstract
The present study explores pupils’ constructed definitions of the concept of function in relation to their abilities in dealing with tasks of functions involving different forms of representations and problem solving tasks. A major concern is also to examine the interrelations between these three ways of thinking about or dealing with the concept of function. The sample of the study consisted of secondary school pupils in Cyprus. A test was developed which involved seven items: one item requested pupils to provide a definition of what function is and the other six items were developed in order to investigate pupils’ ability to transfer information from one representation to another and to solve problems on function. Findings revealed pupils’ difficulties in giving a proper definition for the concept of function and resolving problems on functions involving conversions between diverse modes of representation. Several inconsistencies among pupils’ constructed definitions, their competence to use different representations of functions and their problem solving ability, were also uncovered, indicating lack of flexibility between different ways of approaching functions.
Similar content being viewed by others
References
Bodin, A., Coutourier, R. & Gras, R. (2000). CHIC : Classification Hiérarchique Implicative et Cohésitive-Version sous Windows - CHIC 1.2. Rennes: Association pour la Recherche en Didactique des Mathématiques.
Cheng, P.C.H. (2000). Unlocking conceptual learning in mathematics and science with effective representational systems. Computers and Education, 33, 109–130.
Demetriou, A. (1998). Cognitive development. In A. Demetriou, W. Doise & C. Van Lieshout (Eds.), Life-span developmental psychology (pp. 179–270). Chichester: Wiley.
Dubinsky, E. & Harel, G. (1992). The nature of the process conception of function. In E. Dubinsky & G. Harel (Eds.), The concept of function. Aspects of epistemology and pedagogy (pp. 85–106). United States: The Mathematical Association of America.
Duval, R. (1993). Registres de représentation sémiotique et fonctionnement cognitif de la pensée. Annales de Didactique et de Sciences Cognitives, 5, 37–65.
Duval, R. (2002). The cognitive analysis of problems of comprehension in the learning of mathematics. Mediterranean Journal for Research in Mathematics Education, 1(2), 1–16.
Eisenberg, T. (1992). On the development of a sense for functions. In E. Dubinsky & G. Harel (Eds.), The concept of function.Aspects of epistemology and pedagogy (pp. 153–174). United States: The Mathematical Association of America.
Evangelidou, A., Spyrou, P., Elia, I. & Gagatsis, A. (2004). University students’ conceptions of function. In M. Johnsen Høines & A. Berit Fuglestad (Eds.), Proceedings of the 28th Conference of the International Group for the Psychology of Mathematics Education (vol. 2, pp. 351-358). Bergen, Norway: Bergen University College.
Even, R. (1998). Factors involved in linking representations of functions. The Journal of Mathematical Behavior, 17(1), 105–121.
Gagatsis, A., Elia, I. & Mougi, A. (2002). The nature of multiple representations in developing mathematical relations. Scientia Paedagogica Experimentalis, 39(1), 9-24.
Gagatsis, A., Elia, I. & Andreou, S. (2003). Representations and mathematics learning: Functions and number line, Euclides γ, 59, 5-34 (in Greek).
Gagatsis, A. & Shiakalli, M. (2004). Ability to translate from one representation of the concept of function to another and mathematical problem solving. Educational Psychology, 24(5), 645-657.
Gras, R. (2005). Panorama du developpement de l’ A.S.I. a travers des situations fondatrices. In R. Gras, F. Spagnolo & J. David (Eds.), Proceedings of the Third International Conference I.S.A. Implicative Statistic Analysis (pp. 9–33). Palermo, Italy: Universita degli Studi di Palermo.
Gras, R. & Totohasina, A. (1995). Chronologie et causalité, conceptions sources d’obstacles épistémologiques +//0AyA la notion de probabilité conditionnelle. Recherche en Didactique des Mathématiques, 15(1), 49–95.
Greeno, J.G. & Hall, R.P. (1997). Practicing representation: Learning with and about representational forms. Phi Delta Kappan, 78, 361–367.
Hitt, F. (1998). Difficulties in the articulation of different representations linked to the concept of function. The Journal of Mathematical Behavior, 17(1), 123–134.
Janvier, C. (1998). The notion of chronicle as an epistemological obstacle to the concept of function. Journal of Mathematical Behavior, 17(1), 79–103.
Kaldrimidou, M. & Ikonomou, A. (1998). Factors involved in the learning of mathematics: The case of graphic representations of functions. In H. Stenbring, M.G. Bartolini Bussi & A. Sierpinska (Eds.), Language and communication in the mathematics classroom (pp. 271–288). Reston, Va: NCTM.
Lerman, I.C. (1981). Classification et analyse ordinale des données. Paris: Dunod.
Lesh, R. (1979). Mathematical learning disabilities: Considerations for identification, diagnosis, and remediation. In R. Lesh, D. Mierkiewicz & M. G. Kantowski (Eds.), Applied mathematical problem solving (pp. 111–180). Columbus, OH: ERIC/SMEAR.
Markovits, Z., Eylon, B. & Bruckheimer, M. (1986). Functions today and yesterday. For the Learning of Mathematics, 6(2), 18–28.
Mesa, V. (2004). Characterizing practices associated with functions in middle school textbooks: An empirical approach. Educational Studies in Mathematics, 56, 255–286.
Mousoulides, N. & Gagatsis, A. (2004). Algebraic and geometric approach in function problem solving. In M. Johnsen Hoines & A. Berit Fuglestad (Eds.), Proceedings of the 28th Conference of the International Group for the Psychology of Mathematics Education (vol. 3, pp. 385-392). Bergen, Norway: Bergen University College.
NCTM (2000). Principles and standards for school mathematics. Reston, VA: NCTM.
Norman, A. (1992). Teachers’ mathematical knowledge of the concept of function. In G. Harel & E. Dubinsky (Eds.), The concept of function. Aspects of epistemology and pedagogy, vol. 25, MAA notes (pp. 215–232). Washington, DC: Mathematical Association of America.
Schoenfeld, A.H., Smith, J.P. & Arcavi, A. (1993). Learning: The microgenetic analysis of one student’s evolving understanding of a complex subject matter domain. In R. Glaser (Ed.), Advances in instructional psychology (pp. 55–175). Hillsdale, NJ: Lawrence Erlbaum Associates.
Sfard, A. (1992). Operational origins of mathematical objects and the quandary of reification—the case of function. In E. Dubinsky & G. Harel (Eds.), The concept of function. Aspects of epistemology and pedagogy (pp. 59–84). United States: The Mathematical Association of America.
Sierpinska, A. (1992). On understanding the notion of function. In E. Dubinsky & G. Harel (Eds.), The concept of function. Aspects of epistemology and pedagogy (pp. 25–28). United States: The Mathematical Association of America.
Smith, J.P., diSessa, A.A. & Rocchelle, J. (1993). Misconceptions reconceived: A constructivist analysis of knowledge in transition. Journal of the Learning Sciences, 3, 115–163.
Tall, D. (1991). Advanced mathematical thinking. Dordrecht, The Netherlands: Kluwer Academic Press.
Tall, D. & Vinner, S. (1981). Concept images and concept definition in mathematics with particular reference to limits and continuity. Educational Studies in Mathematics, 12, 151–169.
Vergnaud, G. (1998). A comprehensive theory of representation for mathematics education. Journal of Mathematical Behaviour, 17(2), 167–181.
Vinner, S. (1992). The function concept as a prototype for problems in mathematics learning. In E. Dubinsky & G. Harel (Eds.), The concept of function: Aspects of epistemology and pedagogy (pp. 195–214). United States: Mathematical Association of America.
Vinner, S. & Dreyfus, T. (1989). Images and definitions for the concept of function. Journal for Research in Mathematics Education, 20(4), 266–356.
Vinner, S. & Hershkowitz, R. (1980). Concept images and common cognitive paths in the development of some simple geometrical concepts. In R. Karplus (Ed.), Proceedings of the Fourth International Conference for the Psychology of Mathematics Education (pp.177–184). Berkeley: University of California, Lawrence Hall of Science.
Yerushalmy, M. (1997). Designing representations: Reasoning about functions of two variables. Journal for Research in Mathematics Education, 27(4), 431–466.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Elia, I., Panaoura, A., Eracleous, A. et al. Relations Between Secondary Pupils’ Conceptions About Functions and Problem Solving in Different Representations. Int J Sci Math Educ 5, 533–556 (2007). https://doi.org/10.1007/s10763-006-9054-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10763-006-9054-7