Abstract
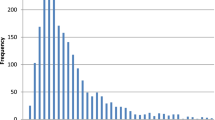
Hospital Length of Stay (LoS) is a valid proxy to estimate the consumption of hospital resources. Average LoS, however, albeit easy to quantify and calculate, can be misleading if the underlying distribution is not symmetric. Therefore the average does not reflect the nature of such underlying distribution and may mask different effects. This paper uses routinely collected data of an Italian hospital patients from different departments over a period of 5 years. This will be the basis for a running example illustrating the alternative models of patients length of stay. The models includes a new density model called Hypergamma. The paper concludes by summarizing these various modelling techniques and highlighting the use of a risk measure in bed planning.




Similar content being viewed by others
References
Artzner P, Delbaen F, Eber JM, Heath D (1999) Coherent measures of risk. Math. Finance 3:203228. Retrieved February 2011
Asmussen S, Nerman O, Olsson M (1996) Fitting phase-type distribution via EM algorithm. Scand J Statist 23:419–441
Bobbio A, Cumani (1992) Computer performance evaluation: 33–46
Cheridito P, Delbaen F, Kupper M (2005) Coherent and convex monetary risk measures for unbounded cádlág processes. Finance Stoch 9:1713–1732
Costa AX (2003) Mathematical modelling and simulation for planning critical care capacity. Anaesthesia 58:320327
Delbaen F (2002) Coherent measures of risk on general probability spaces. In: Advances in finance and stochastics. Essays in honour of dieter sondermann. Springer-Verlag
Fackrell M (2008) Modelling healthcare system with phase-type distributions Health Care Manage Sci
Faddy MJ, McClean SI (1999) Analysing data on length of stay of hospital patients using phase-type distribution. Appl Stoch Models Bus Ind 15:311–317
Fang KT, Yang Y (1994) Number-theoretic methods in statistics. Chapman&Hall, London
Harper P, Shahani A (2002) Modelling for the planning and management of bed capacities in hospitals. J Opl Res Soc 53:1118
He Q, Zhang H (2005) A note on unicyclic representation of phase-type distributions. Stoch Models 21:465– 483
McClean SI, Millard PH (1993) Patterns of length of stay after admission in geriatric medicine: an event history approach. Stat 42:263–274
Millard PH (1994) Current measures and their defects. In: Modelling hospital resource use: a different approach to the planning and control of health care systems Millard P H, McClean S I (eds), Royal Society of Medicine, London
Neuts MF (1975) Probability distributions of phase-type. In: Liber amicorum Prof. Emeritus H. Florin, Department of Mathematics, University of Louvain, Louvain, pp 173206
Niederreiter H (1992) Random number generation and quasi-monte carlo methods. SIAM, Philadelphia
O’Cinneide CA (1999) Phase-type distributions: open problems and few properties. Commun Stat Stoch Models 15:731–757
Ross SM Introduction to probability models, 5th edn. Academic, San Diego
Ross SM Stochastic process, Second Edition. Wiley
Vasilakis C, Marshall AH (2005) Modelling nationwide hospital length of stay: opening the black box. J Oper Res Soc 56:862869
Acknowledgments
This research is supported in part by the administrative division of the hospital Campus Bio-Medico.
Author information
Authors and Affiliations
Corresponding author
Appendix section
Appendix section
A function \(g:\mathbb {R}\rightarrow \mathbb {R}\) is a probability density function of a continuous random variable if
-
g is a non-negative Lebesgue-integrable function;
-
\({\int }_{-\infty }^{+\infty }\, g(x)\, dx=1\).
Then we have the following result
Proposition 1
Let g be a probability density function. For every α 1 , α 2 , …, α n ≥0 with α 1 +α 2 +⋯+α n =1, and ł 1 , ł 2 , …, ł n > 0, the function
is a probability density function.
Proof
It suffices to prove that \({\int }_{\mathbb {R}}\, h(\tau )\, d\tau =1\). In fact, we have
For any integral, in the sum, we apply the change of variable τ = −s/λ i . Thus
In the same way it is possible to evaluate the mean and the variance of a random variable distributed according to a Hypergamma density function:
Here the moment generating function is well defined on the interval t < 𝜃min(λ 1, λ 2, . . . , λ n ).
Rights and permissions
About this article
Cite this article
Papi, M., Pontecorvi, L. & Setola, R. A new model for the length of stay of hospital patients. Health Care Manag Sci 19, 58–65 (2016). https://doi.org/10.1007/s10729-014-9288-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10729-014-9288-9