Complete solution of the Einstein field equations for a spherical distribution of polytropic matter

Abstract

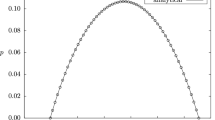
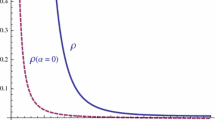
We determine the complete solution of the Einstein field equations for the case of a spherically symmetric distribution of gaseous matter, characterized by a polytropic equation of state. We show that the field equations automatically generate two sharp boundaries for the gas, an inner one and an outer one, given by radial positions $r_{1}$ and $r_{2}$, and thus define a shell of gaseous matter outside of which the energy density is exactly zero. Hence this shell is surrounded by an outer vacuum region, and surrounds an inner vacuum region. Therefore, the solution is given in three regions, one being the well-known analytical Schwarzschild exterior solution in the outer vacuum region, one being determined analytically in the inner vacuum region, and one being determined partially analytically and partially numerically, within the matter region, between the two boundary values $r_{1}$ and $r_{2}$ of the Schwarzschild radial coordinate r. This solution is therefore somewhat similar to the one previously found for a spherically symmetric shell of liquid fluid, and is in fact exactly the same in the cases of the inner and outer vacuum regions. The main difference is that here the boundary values $r_{1}$ and $r_{2}$ are not chosen arbitrarily, but are instead determined by the dynamics of the system. As was shown in the case of the liquid shell, also in this solution there is a singularity at the origin, that just as in that case does not correspond to an infinite concentration of matter, but in fact to zero matter energy density at the center. Also as in the case of the liquid shell, the spacetime within the spherical cavity is not flat, so that there is a non-trivial gravitational field there, in contrast with Newtonian gravitation. This inner gravitational field has the effect of repelling matter and energy away from the origin, thus avoiding a concentration of matter at that point.