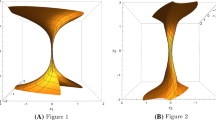
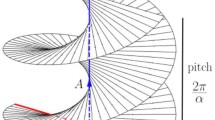
Abstract
The purpose of this paper is to construct one parameter families of embedded, screw motion invariant minimal surfaces in \({\mathbb {R}}^3\) which limit to parking garage structures. We construct such surfaces by defining Weierstrass data on the quotient and closing the periods. In the nodal limit, the periods reduce to algebraic balance equations for the locations of the helicoidal nodes. For any configuration of nodes that solve the equations and satisfy a nondegeneracy condition, we regenerate to obtain a family of surfaces near the limit. We thus prove the existence of many new examples of surfaces near the nodal limit, with helicoidal or planar ends. Among these are candidates for genus g helicoids distinct from those currently known. We do not require any symmetry for the solutions of the balance equations, which suggests the existence of helicoidal surfaces only symmetric with respect to screw motions. This introduces new directions for the study and classification of screw motion invariant surfaces.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Data availability
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Karcher, H.: Embedded minimal surfaces derived from Scherk’s examples. Manuscripta Math. 62, 83–114 (1988)
Fischer, W., Koch, E.: On 3-periodic minimal surfaces with non-cubic symmetry. Zeitschrift für Kristallographie 183, 129–152 (1988)
Lynker, A.: Einfach periodische elliptische minimalflächen. Diplomarbeit Bonn (1993)
Callahan, M., Hoffman, D., Karcher, H.: A family of singly-periodic minimal surfaces invariant under a screw motion. Exp. Math. 2, 157–182 (1993)
Weber, M., Hoffman, D., Wolf, M.: An embedded genus-one helicoid. Ann. Math. 169(2), 347–448 (2009)
Hoffman, D., Traizet, M., White, B.: Helicoidal minimal surfaces of prescribed genus. Acta Mathematica 216, 217–323 (2016)
Meeks, W.H., III., Rosenberg, H.: The geometry of periodic minimal surfaces. Comment. Math. Helvetici 68, 538–578 (1993)
Traizet, M., Weber, M.: Hermite polynomials and helicoidal minimal surfaces. Inv. Math. 161, 113–149 (2005)
Choe, J., Soret, M.: Nonexistence of certain complete minimal surfaces with planar ends. Commentarii Mathematici Helvetici 75, 189–199 (2000)
Traizet, M.: An embedded minimal surface with no symmetries. J. Differ. Geom. 60, 103–153 (2002)
Aref, H.: Vortices and polynomials. Fluid Dyn. Res. 39, 5–23 (2007)
Acknowledgements
We would like to thank Matthias Weber for his invaluable advice and discussions, as well as Ramazan Yol and Hao Chen for their helpful contributions. We are also grateful to the referee for his valuable corrections and suggestions.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Freese, D. Screw motion invariant minimal surfaces from gluing helicoids. Geom Dedicata 217, 44 (2023). https://doi.org/10.1007/s10711-023-00774-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10711-023-00774-2