Infinitely many roots of unity are zeros of some Jones polynomials

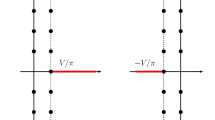
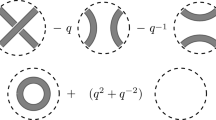Abstract

Let $N=2n^2-1$ or $N=n^2+n-1$, for any $n\ge 2$. Let $M=\frac{N-1}{2}$. We construct families of prime knots with Jones polynomials $(-1)^M\sum _{k=-M}^{M} (-1)^kt^k$. Such polynomials have Mahler measure equal to 1. If N is prime, these are cyclotomic polynomials $\Phi _{2N}(t)$, up to some shift in the powers of t. Otherwise, they are products of such polynomials, including $\Phi _{2N}(t)$. In particular, all roots of unity $\zeta _{2N}$ occur as roots of Jones polynomials. We also show that some roots of unity cannot be zeros of Jones polynomials.