On cusp regions associated to screw-parabolic maps

Abstract

Erlandsson and Zakeri gave a very precise description of the Margulis region associated to cusps of hyperbolic 4-manifolds associated to screw-parabolic maps. We give some bounds on the asymptotic shape of these regions that improve on the results of Erlandsson and Zakeri. We also describe similar regions coming from work of Waterman. Finally, we generalise these results to complex hyperbolic 2-space.

1 Introduction

1.1 Background and motivation

Let $\Gamma$ be a discrete subgroup of $\mathrm{PSL}(2,{{\mathbb {C}}})$ and suppose that $\Gamma _\infty$, the stabiliser of $\infty$ in $\Gamma$, contains the translation $A(z)=z+t$ where, without loss of generality, t is a positive real number. The Margulis lemma implies that there is a universal $\varepsilon >0$ so that the horoball (based at $\infty$) in $\mathbf{H}^3_{{\mathbb {R}}}$ where the hyperbolic translation length of A is less than $\varepsilon$ has the property that this horoball is disjoint from all its images under elements of $\Gamma$ not fixing $\infty$. That is, this horoball is precisely invariant under $\Gamma _\infty$ in $\Gamma$. The Shimizu-Leutbecher lemma, which is a particular case of Jørgensen’s inequality, quantifies this statement. Specifically, it says that if $\Gamma _\infty$ contains $A(z)=z+t$ then the horoball $H_t=\bigl \{(x_1,x_2,x_3)\, :\, x_3>t\bigr \}$ is precisely invariant under $\Gamma _\infty$ in $\Gamma$.

In higher dimensions there are parabolic isometries fixing $\infty$ that are not translations. These screw motions translate along an axis and rotate the orthogonal complement of this axis. Of particular interest are those where the rotation has infinite order. Given such a screw motion A acting on $\mathbf{H}^n_{{\mathbb {R}}}$ with $n\ge 4$, Ohtake [9] showed that for any horoball H in $\mathbf{H}^n_{{\mathbb {R}}}$, one may construct a discrete group $\Gamma$ containing A and an element B so that $B(H)\cap H\ne \emptyset$. The key point is the centre of the isometric sphere of B must be a long way from from the axis of rotation of A. Waterman [12] quantified this and showed that the permissible radius R of an isometric sphere is bounded by a function that asymptotically is a linear function of the distance r from the axis of rotation. A sub-horospherical region based at $\infty$ is a region contained in a horoball in $\mathbf{H}^n_{{\mathbb {R}}}$ based at $\infty$ but which does not itself contain a horoball. It is straightforward to use Waterman’s result to construct a precisely invariant sub-horospherical region whose boundary function is asymptotically a linear function of the distance from the axis of rotation as well; see Proposition 3.8 or [3].

In a beautiful paper, Erlandsson and Zakeri [2], following earlier work by Susskind [11], have considered the case of real hyperbolic 4-space $\mathbf{H}^4_{{\mathbb {R}}}$. They consider discrete groups containing a screw parabolic map A with rotation angle $2\pi \alpha$, where $\alpha$ is irrational. By examining the continued fraction expansion of $\alpha$, they are able to show that there is a precisely invariant sub-horospherical region whose boundary function grows asymptotically like the square root of the distance to the rotation axis.

Roughly speaking, the argument is the following. The sub-horospherical regions corresponding to a power $A^q$ of A is a bowl whose cross-section is a hyperbola. As the powers q of A increase, so the heights of the centres of these bowls increase. However, the closer $2\pi q\alpha$ comes to being a multiple of $2\pi$, the flatter the bowls become. Therefore, very far from the axis of A, a better bound may be obtained by considering extremely flat bowls that may be very high (see Figure 1 of Susskind [11] for example). The precise relationship between the size of q with the height and the degree of flatness of the bowls is determined by the continued fraction expansion of the irrational number $\alpha$.

The sub-horospherical region constructed by Erlandsson and Zakeri is quite complicated and depends heavily on the continued fraction expansion of the rotation angle. Therefore, they are only able to give the asymptotic behaviour of the boundary of their sub-horospherical region, mostly without constructing actual functions or constants. The purpose of this paper is to give a sub-horospherical region that is slightly smaller than the one constructed by Erlandsson and Zakeri, but which is given by a reasonably well behaved function. This enables us to give much better information about the asymptotic behaviour of such a region.

Precisely invariant sub-horospherical regions coming from generalisations of Shimizu’s lemma in complex hyperbolic space $\mathbf{H}^2_{{\mathbb {C}}}$ have been given by Cao and Parker [1] (see also Jiang and Parker [7] and Kamiya and Parker [8] for different statements along similar lines). It is natural to ask whether Erlandsson and Zakeri’s methods can be applied in this case. This was done by Ren et al. [10], who give a sub-horospherical region whose boundary is asymptotically linear in the distance to the axis. We use similar methods to the real hyperbolic case to give complex hyperbolic estimates which improve those given by Ren, Wang and Xie. We also exhibit an unbounded sequence of points in the Margulis region that all lie on the same horosphere.

1.2 Summary of results for real hyperbolic 4-space

Suppose that $A\in \mathrm{Isom}(\mathbf{H}^4_{{\mathbb {R}}})$ is parabolic. This means its only fixed point lies on $\partial \mathbf{H}^4_{{\mathbb {R}}}$. Using the upper half space model of $\mathbf{H}^4_{{\mathbb {R}}}=\bigl \{(x_1,x_2,x_3,x_4)\in {{\mathbb {R}}}^4\ :\ x_4>0\bigr \}$, we may assume without loss of generality that A fixes the point $\infty$. This means that it acts on the upper half space as a Euclidean isometry without fixed points. Such maps are either translations or else they are screw motions, which means there is a Euclidean line $\ell \in \partial \mathbf{H}^4_{{\mathbb {R}}}$ so that A translates along $\ell$ and rotates the orthogonal complement of $\ell$. Applying Euclidean isometries if necessary, we may assume that $\ell$ is the $x_3$ axis. In which case, it is convenient to use cylindrical polar coordinates $(r,\theta ,v,u)$, which correspond to $\bigl (r\cos (\theta ),r\sin (\theta ),v,u\bigr )\in {{\mathbb {R}}}^4$. In these coordinates:

$$\begin{aligned} \mathbf{H}^4_{{\mathbb {R}}}=\Bigl \{ (r,\theta ,v,u)\ :\ u>0\Bigr \}. \end{aligned}$$

Using the normalisation given above, we may define the screw parabolic map $A=A_{\alpha ,t}:\mathbf{H}^4_{{\mathbb {R}}}\longrightarrow \mathbf{H}^4_{{\mathbb {R}}}$ by

$$\begin{aligned} A=A_{\alpha ,t}:(r,\theta ,v,u)\longmapsto (r,\theta +2\pi \alpha ,v+t,u). \end{aligned}$$

(1)

Note that this differs from equation (7) of [2] since Erlandsson and Zakeri assume that $t=1$. We prefer to keep t arbitrary and to give formulae that are homogeneous in r, v (that is in t) and u. Let $U_{q\alpha ,qt}$ be the region in $\mathbf{H}^4_{{\mathbb {R}}}$ where, for an integer $q\ge 1$, the map $A^{\pm q}$ moves points by a hyperbolic distance at most $\varepsilon$. This region is given by:

$$\begin{aligned} U_{q\alpha ,qt}=\Bigl \{(r,\theta ,v,u)\in \mathbf{H}^4_{{\mathbb {R}}}\ :\ u>c(\varepsilon )\sqrt{4\sin ^2(\pi q\alpha )r^2+q^2t^2}\Bigr \} \end{aligned}$$

where $c(\varepsilon )=1/2\sinh (\varepsilon /2)$; compare equation (9) of [2]. We take $\varepsilon$ to be (at most) the Margulis constant for $\mathbf{H}^4_{{\mathbb {R}}}$ (see Sect. 3.1 for detailed definitions of the above quantities).

Following Erlandsson and Zakeri (equation (10) of [2]) define the boundary function ${{\mathcal {B}}}_{\alpha ,t}(r)$ by

$$\begin{aligned} {{\mathcal {B}}}_{\alpha ,t}(r)=c(\varepsilon ) \inf _{q\ge 1} \sqrt{4\sin ^2(\pi q\alpha )r^2+q^2t^2} \end{aligned}$$

(2)

(Note that this formula is homogeneous in r, v and u since t behaves like v and ${{\mathcal {B}}}_{\alpha ,t}(r)$ behaves like u. More precisely, for all $k>0$ we have ${{\mathcal {B}}}_{\alpha ,kt}(kr)=k{{\mathcal {B}}}_{\alpha ,t}(r)$.) From this, we define the sub-horospherical region

$$\begin{aligned} T_{\alpha ,t}=\bigcup _{q\ge 1}U_{q\alpha ,qt} =\Bigl \{(r,\theta ,v,u)\in \mathbf{H}^4_{{\mathbb {R}}}\ :\ u>{{\mathcal {B}}}_{\alpha ,t}(r)\Bigr \}. \end{aligned}$$

The geometrical meaning of $T_{\alpha ,t}$ is that the point $(r,\theta ,v,u)$ lies in $T_{\alpha ,t}$ if and only if there is a power $A^q$ of A moving this point a hyperbolic distance at most $\varepsilon$. In other words, $T_{\alpha ,t}$ is one component of the corresponding Margulis region (see Sect. 3.2 for more details). Erlandsson and Zakeri prove the following theorem about the boundary function:

Theorem 1.1

(Theorem A of Erlandsson and Zakeri [2])

• (1) For every irrational $\alpha$ and $t>0$, the boundary function ${{\mathcal {B}}}_{\alpha ,t}$ satisfies the asymptotic upper bound

  $$\begin{aligned} {{\mathcal {B}}}_{\alpha ,t}(r)\le \hbox {const. }\sqrt{r} \end{aligned}$$

  for large r. Moreover, when $r\ge \sqrt{2}\,q_7^2$ one can take the constant to be at most

  $$\begin{aligned} c(\varepsilon )\sqrt{(8\pi ^2+1)24\pi t/\sqrt{3}}<1000\sqrt{t} \end{aligned}$$

  where $\varepsilon$ is the Margulis constant and $c(\varepsilon )=1/\bigl (2\sinh (\varepsilon /2)\bigr )$.

• (2) If $\alpha$ is Diophantine of exponent $\nu \ge 2$, then ${{\mathcal {B}}}_{\alpha ,t}$ satisfies the following lower bound for large r

  $$\begin{aligned} {{\mathcal {B}}}_{\alpha ,t}(r)\ge \hbox {const. }r^{1/(2\nu -2)}. \end{aligned}$$

Note that in both cases the constant depends on t, but this is not immediately apparent from [2] since the authors have normalised $t=1$. Using scaling by loxodromic maps fixing $\infty$ it is clear how to make the constants depend on t so that the formulae are homogeneous (that is ${{\mathcal {B}}}_{\alpha ,kt}(kr)=k{{\mathcal {B}}}_{\alpha ,t}(r)$ for all $k>0$).

As well as the Margulis region, we want to have a region which does not depend on $\varepsilon$. We show, Proposition 3.8, that for any discrete group $\Gamma$ with $\Gamma _\infty =\langle A\rangle$, for all $q\in {{\mathbb {Z}}}-\{0\}$ with $4|\sin (\pi q\alpha )|<1/2$ the sub-horospherical region ${\widehat{U}}_{q\alpha ,qt}$ is precisely invariant under $\Gamma _\infty$ in $\Gamma$ where

$$\begin{aligned} {\widehat{U}}_{q\alpha ,qt}=\left\{ (r,\theta ,v,u)\in \mathbf{H}^4_{{\mathbb {R}}}\ :\ u>\sqrt{\frac{4\sin ^2(\pi q\alpha )r^2+q^2t^2}{\Delta _{{\mathbb {R}}}\bigl (4|\sin (\pi q\alpha )|\bigr )}}. \right\} \end{aligned}$$

where $\Delta _{{\mathbb {R}}}(X)$ is the following function of $X\in [0,1/2]$:

$$\begin{aligned} \Delta _{{\mathbb {R}}}(X)=\frac{\bigl (1+\sqrt{1-2X}\bigr )^2-X^2}{4}, \end{aligned}$$

Now let ${\widehat{T}}_{\alpha ,t}$ be the union of the regions ${\widehat{U}}_{q\alpha ,qt}$ over all $q\ge 1$ for which $4|\sin (\pi q\alpha )|<1/2$. That is

$$\begin{aligned} {\widehat{T}}_{\alpha ,t}=\bigcup _q{\widehat{U}}_{q\alpha ,qt} =\Bigl \{(r,\theta ,v,u)\in \mathbf{H}^4_{{\mathbb {R}}}\ :\ u>\widehat{{\mathcal {B}}}_{\alpha ,t}(r)\Bigr \} \end{aligned}$$

where

$$\begin{aligned} \widehat{{\mathcal {B}}}_{\alpha ,t}(r)=\inf _q \sqrt{\frac{4\sin ^2(\pi q\alpha )r^2+q^2t^2}{\Delta _{{\mathbb {R}}}\bigl (4|\sin (\pi q\alpha )|\bigr )}}. \end{aligned}$$

(3)

and the infimum is taken over all integers $q\ge 1$ for which $4|\sin (\pi q\alpha )|<1/2$.

A key observation (see Lemma 3.1) is that the infimum in Eqs. (2) and (3) is attained when q is the denomenator $q_n$ of one of the rational convergents of $\alpha$. These denominators are a strictly increasing sequence of integers. Given $N\in {{\mathbb {N}}}$, it will be useful to consider a constant $\lambda _N$ so that $q_n/q_{n+1}\le \lambda _N$ for all $n\ge N$. Since the $q_n$ are increasing, we may always take $\lambda _N=1$. See Sect. 2 below for more about the properties of rational convergents and Sect. 3.3 for more about $\lambda _N$, together with some examples.

Theorem 1.2

Let $\varepsilon$ denote the Margulis constant for $\mathbf{H}^4_{{\mathbb {R}}}$ and let $c(\varepsilon )=1/\bigl (2\sinh (\varepsilon /2)\bigr )$. Let $A=A_{\alpha ,t}:\mathbf{H}^4_{{\mathbb {R}}}\longrightarrow \mathbf{H}^4_{{\mathbb {R}}}$ be given by (1) where $\alpha$ is irrational and $t>0$. Let $p_n/q_n$ for $n\in {{\mathbb {N}}}$ be the rational convergents of $\alpha$. Given $N\in {{\mathbb {N}}}$, suppose that $\lambda _N\in (0,1]$ is a constant for which $q_n/q_{n+1}\le \lambda _N$ for all $n\ge N$. Let ${{\mathcal {B}}}_{\alpha ,t}(r)$ and $\widehat{{\mathcal {B}}}_{\alpha ,t}(r)$ be the boundary functions defined by (2) and (3). Then

• (1) For all $r\ge q_N^2t/2\pi$ we have

  $$\begin{aligned} {{\mathcal {B}}}_{\alpha ,t}(r)< c(\varepsilon )\sqrt{(1+\lambda _N^2)2\pi t}\,\sqrt{r}. \end{aligned}$$

• (2) Let $\alpha$ be Diophantine of exponent $\nu \ge 2$ and let K be the associated constant defined in (12) below. Then

  $$\begin{aligned} {{\mathcal {B}}}_{\alpha ,t}(r) >\frac{c(\varepsilon )(4K)^{1/\nu }\nu ^{1/2}t^{(\nu -1)/\nu }}{(\nu -1)^{(\nu -1)/2\nu }}\ r^{1/\nu }. \end{aligned}$$

  In particular, if $\nu =2$ then

  $$\begin{aligned} {{\mathcal {B}}}_{\alpha ,t}(r) >c(\varepsilon )\sqrt{8Kt}\,\sqrt{r}. \end{aligned}$$

• (3) Suppose that N is chosen so that $q_N>8\pi$. Then for all $r\ge q_N^2t/2\pi$ we have

  $$\begin{aligned} \widehat{{\mathcal {B}}}_{\alpha ,t}(r)< & {} \sqrt{\frac{(1+\lambda _N^2)2\pi tr}{\Delta _{{\mathbb {R}}}\bigl (2\sqrt{2\pi t/r}\bigr )}} \\= & {} \sqrt{1+\lambda _N^2}\Bigl (\sqrt{2\pi t}\sqrt{ r}+2\pi t+O(r^{-1/2})\Bigr ). \end{aligned}$$

• (4) Let $r_0>0$ be any positive constant. Then there exists a discrete group $\Gamma$ for which $\Gamma _\infty =\langle A\rangle$ and a point $(r,\theta ,v,u)\in \mathbf{H}^2_{{\mathbb {R}}}$ with $r>r_0$ and $u>\sqrt{t/2}\sqrt{r}$ that cannot lie in any precisely invariant sub-horospherical region for $\Gamma$.

We prove the different parts of this theorem in separate sections. Part (1) is Proposition 3.3, part (2) is Proposition 3.5, part (3) is Proposition 3.9 and part (4) is Proposition 3.6.

Remark 1.3

• (1) Comparing the constants from Theorem 1.1 (1) and Theorem 1.2 (1) with $\lambda _N=1$, we have

  $$\begin{aligned} \frac{\sqrt{(8\pi ^2+1)24\pi t/\sqrt{3}}}{\sqrt{4\pi t}}= \sqrt{(8\pi ^2+1)2\sqrt{3}}=9.51454\ldots . \end{aligned}$$

  Therefore Theorem 1.2 (1) improves Theorem 1.1 (1) by a factor of $9.51454\ldots$.

• (2) Note that for $\nu >2$ we have $r^{1/\nu }>r^{1/(2\nu -2)}$ for all $r>1$, and so, for Diophantine $\alpha$ with exponent greater than 2, Theorem 1.2 (2) improves the power of r in Theorem 1.1 (2).

• (3) The example in Theorem 1.2 (4) and the upper bound from Theorem 1.2 (1) both give a power of $r^{1/2}$. Thus this exponent is sharp for any precisely invariant sub-horospherical region. The upper bound follows from Erlandsson and Zakeri [2] and they also give an unbounded sequence of points on the boundary of the Margulis region where the boundary ${{\mathcal {B}}}_{\alpha ,t}(r)$ grows like $r^{1/2}$. However, they do not rule out the possibility that some other precisely invariant sub-horospherical region has slower growth than $r^{1/2}$.

• (4) The examples in Theorem 1.2 (4) only gives points (r, 0, 0, u) lying outside all precisely invariant sub-horospherical regions for certain values of r. For $\nu >2$, the discrepancy between the exponents of r in Theorem 1.2 (2) and (4) is a measure of how the boundary function ${{\mathcal {B}}}_{\alpha ,t}(r)$ oscillates.

1.3 Summary of results for complex hyperbolic 2-space

A map $A\in \mathrm{Isom}(\mathbf{H}^2_{{\mathbb {C}}})$ is parabolic if it has a unique fixed point that lies on $\partial \mathbf{H}^2_{{\mathbb {C}}}$. Using the Siegel domain model of complex hyperbolic 2-space we may assume, without loss of generality, that A fixes $\infty$. This means that A is either a Heisenberg translation or a screw parabolic map. In the latter case there is a chain $\ell$ through $\infty$ in $\partial \mathbf{H}^2_{{\mathbb {C}}}$ so that A translates along $\ell$ and rotates the contact plane at all points of $\ell$. We give $\mathbf{H}^2_{{\mathbb {C}}}$ polar horospherical polar coordinates:

$$\begin{aligned} \mathbf{H}^2_{{\mathbb {C}}}=\Bigl \{(r,\theta ,v,u)\in {{\mathbb {C}}}\times {{\mathbb {R}}}^2\ :\ u>0\Bigr \}. \end{aligned}$$

Then, without loss of generality, we may suppose that $\ell$ is the v-axis.

Using the normalisation above, we can then define the screw parabolic map $A=A_{\alpha ,t}:\mathbf{H}^2_{{\mathbb {C}}}\longrightarrow \mathbf{H}^2_{{\mathbb {C}}}$ by

$$\begin{aligned} A=A_{\alpha ,t}:(r,\theta ,v,u)\longmapsto (r,\theta +2\pi \alpha ,v+t,u). \end{aligned}$$

(4)

Because of the way horospherical coordinates in complex hyperbolic space scale, we now need formulae that are homogeneous in $r^2, v$ and u. We consider the following sub-horospherical region

$$\begin{aligned} U_{q\alpha ,qt}^{{\mathbb {C}}} =\Bigl \{(r,\theta ,v,u)\in \mathbf{H}^2_{{\mathbb {C}}}\ :\ u>c(\varepsilon /2)^2 \bigl (4\sin (\pi q\alpha )r^2+qt\bigr ) \Bigr \}. \end{aligned}$$

This is contained in the region where $A^q$ has Bergman translation length at most $\varepsilon$. Taking the union over such regions for all powers of A gives

$$\begin{aligned} T^{{\mathbb {C}}}_{\alpha ,t}=\bigcup _{q\ge 1}U_{q\alpha ,qt}^{{\mathbb {C}}} =\Bigl \{(r,\theta ,v,u)\in \mathbf{H}^2_{{\mathbb {C}}}\ :\ u>{{\mathcal {B}}}^{{\mathbb {C}}}_{\alpha ,t}(r)\Bigr \} \end{aligned}$$

where ${{\mathcal {B}}}^{{\mathbb {C}}}_{\alpha ,t}$ is the complex hyperbolic boundary function

$$\begin{aligned} {{\mathcal {B}}}^{{\mathbb {C}}}_{\alpha ,t}(r)=c(\varepsilon /2)^2 \inf _{q\ge 1} \bigl (4\sin (\pi q\alpha )r^2+qt\bigr ). \end{aligned}$$

(5)

In this case, the statement about homogeneity is that ${{\mathcal {B}}}_{\alpha ,k^2t}^{{\mathbb {C}}}(kr)=k^2{{\mathcal {B}}}_{\alpha ,t}^{{\mathbb {C}}}(r)$ for all $k>0$.

We also have versions of these sets that do not depend on $\varepsilon$. Define

$$\begin{aligned} {\widehat{T}}^{{\mathbb {C}}}_{\alpha ,t}=\Bigl \{(r,\theta ,v,u)\in \mathbf{H}^2_{{\mathbb {C}}}\ :\ u>\widehat{{\mathcal {B}}}^{{\mathbb {C}}}_{\alpha ,t}(r)\Bigr \} \end{aligned}$$

where $\widehat{{\mathcal {B}}}^{{\mathbb {C}}}_{\alpha ,t}$ is the boundary function

$$\begin{aligned} \widehat{{\mathcal {B}}}^{{\mathbb {C}}}_{\alpha ,t}(r)=\inf _q \frac{4\sin (\pi q\alpha )r^2+qt}{\Delta _{{\mathbb {C}}}(4|\sin (\pi q\alpha )|)} \end{aligned}$$

(6)

and the infimum is taken over all integers $q\ge 1$ for which $4|\sin (\pi q\alpha )|<(\sqrt{2}-1)^2$. Here

$$\begin{aligned} \Delta _{{\mathbb {C}}}(X)=\frac{1-3X+\sqrt{1-6X+X^2}}{2}. \end{aligned}$$

Ren, Wang and Xie gave the following complex hyperbolic version of Theorem 1.1:

Theorem 1.4

(Theorem 5 of Ren et al. [10]) For every irrational $\alpha$ and $t>0$ the boundary function ${{\mathcal {B}}}_{\alpha ,t}^{{\mathbb {C}}}$ satisfies the asymptotic upper bound

$$\begin{aligned} {{\mathcal {B}}}_{\alpha ,t}^{{\mathbb {C}}}(r) \le \hbox {const. }r. \end{aligned}$$

Moreover, one can take the constant to be at most $1.7\times 10^6\sqrt{t}$ when $r\ge 2^{1/4}\,q_7$.

Our main results can be combined as:

Theorem 1.5

Let $\varepsilon >0$ be the Margulis constant for $\mathbf{H}^2_{{\mathbb {C}}}$ and let $c(\varepsilon /2)=1/\bigl (2\sinh (\varepsilon /4)\bigr )$. Let $A=A_{\alpha ,t}:\mathbf{H}^2_{{\mathbb {C}}}\longrightarrow \mathbf{H}^2_{{\mathbb {C}}}$ be given by (4) where $\alpha$ is irrational and $t>0$. Let $p_n/q_n$ be the rational convergents of $\alpha$. Given $N\in {{\mathbb {N}}}$, let $\lambda _N\in (0,1]$ be a constant for which $q_n/q_{n+1}\le \lambda _N$ for all $n\ge N$. Let ${{\mathcal {B}}}_{\alpha ,t}^{{\mathbb {C}}}$ and $\widehat{{\mathcal {B}}}_{\alpha ,t}^{{\mathbb {C}}}$ be the boundary functions defined by (5) and (6). Then

• (1) For all $r\ge q_N\sqrt{t/4\pi }$ we have

  $$\begin{aligned} {{\mathcal {B}}}_{\alpha ,t}^{{\mathbb {C}}}(r)<c(\epsilon /2)^2(1+\lambda _N)2\sqrt{\pi t}\,r. \end{aligned}$$

• (2) Let $u_0=4c(\varepsilon /2)^2\lambda _N t$. Then there is an unbounded sequence of points on the horosphere $H_{u_0}$ of height $u_0$ that lie in the Margulis region. That is, for any positive constant $r_0$ there exists an integer $q\ge 1$ and a point $z=(r,\theta ,v,u_0)$ on $H_{u_0}$ so that $r>r_0$ and $\rho \bigl (A^q(z),z\bigr )\le \varepsilon$.

• (3) Let N be chosen so that $q_N>4\pi /\bigl (\sqrt{2}-1\bigr )^2$. For all $r\ge q_N\sqrt{t/4\pi }$ we have

  $$\begin{aligned} \widehat{{\mathcal {B}}}_{\alpha ,t}^{{\mathbb {C}}}(x)< & {} \frac{(1+\lambda _N)2\sqrt{\pi t}\,r}{\Delta _{{\mathbb {C}}}(2\sqrt{\pi t}/r)} \\= & {} (1+\lambda _N)\bigl (2\sqrt{\pi t}\,r+12\pi t\bigr )+O(r^{-1}). \end{aligned}$$

The proofs will be broken up into separate pieces. Part (1) is Proposition 4.3, part (2) is Proposition 4.5 and part (3) is Proposition 4.8.

Remark 1.6

For certain powers q the translation length of $A^q$ is not a monotone function. The points constructed in Theorem 1.5 (2) only exist for particular values of r, which roughly correspond to the minima of these translation lengths for some values of q. In Proposition 4.6 we give another unbounded sequence of points lying on horospheres whose heights tend to infinity with the property that the Bergman translation length of $A^{q_n}$ at all these points is greater than the Margulis constant for all partial convergents $p_n/q_n$ of $\alpha$. However, unlike for real hyperbolic space, we do not know that the minimum Bergman translation length must be attained for one of these powers. This means we cannot construct groups analogous to those in Theorem 1.2 (4). Hence, it is not clear what the optimum exponent of r is among all precisely invariant subhorospherical regions. Theorem 1.5 only says that this exponent lies in the interval [0, 1].

2 Continued fractions and Diophantine approximation

One of the main tasks in our proofs is to estimate $|\sin (\pi q\alpha )|$ for fixed irrational $\alpha$ as $q\in {{\mathbb {N}}}$ varies. Following Erlandsson and Zakeri, we do this using the rational convergents coming from the continued fraction expansion of $\alpha$. We now review the facts about continued fractions and Diophantine approximation that we need. This material is well known and may be found in many books. Our main reference is Hardy and Wright [5].

For any real number $\alpha$ the continued fraction expansion of $\alpha$ is

$$\begin{aligned} \alpha =a_0+\frac{1}{a_1+\frac{1}{a_2+\frac{1}{a_3+\cdots }}} \end{aligned}$$

where $a_n\in {{\mathbb {Z}}}$ and $a_n\ge 0$ for all $n\ge 1$. We write this expansion as

$$\begin{aligned} \alpha =[a_0;a_1,a_2,a_3,\ldots ]. \end{aligned}$$

The real number $\alpha$ is rational if and only if the continued fraction expansion has finitely many terms, that is some $a_N=0$. In what follows, we always assume $\alpha$ is irrational, which means $\alpha$ has an infinite continued fraction expansion, and so $a_n\ge 1$ for all $n\ge 1$.

Given an irrational number $\alpha$ we can construct a sequence of rational numbers $p_n/q_n$, called the rational convergents of $\alpha$, by truncating the continued fraction expansion $\alpha =[a_0;a_1,a_2,a_3,\ldots ]$ after finitely many steps. That is

$$\begin{aligned} p_n/q_n=[a_0;a_1,a_2,\,\ldots ,a_n]. \end{aligned}$$

(7)

In particular, $p_0/q_0=a_0$ and $p_1/q_1=a_0+1/a_1=(a_0a_1+1)/a_1$. Thus $q_0=1$ and $q_1=a_1\ge 1$. The rational convergents oscillate around $\alpha$. In particular, Theorems 152 and 154 of Hardy and Wright [5] imply that for all $m\ge 1$

$$\begin{aligned} \frac{p_{2m}}{q_{2m}}<\frac{p_{2m+2}}{q_{2m+2}}<\alpha< \frac{p_{2m+1}}{q_{2m+1}}<\frac{p_{2m-1}}{q_{2m-1}}. \end{aligned}$$

(8)

It is straightforward to verify that the rational convergents satisfy the following recursion relations for $n\ge 2$:

$$\begin{aligned} p_n=a_n p_{n-1} +p_{n-2}, \qquad q_n=a_n q_{n-1} + q_{n-2}. \end{aligned}$$

The following lemma is a simple consequence of the above recursion property:

Lemma 2.1

• (1) $q_{2m}\ge 2^{m}$ and $q_{2m+1}\ge 2^{m}$ for all $m\ge 0$.

• (2) If $a_n\ge a\ge 2$ for all $n\ge N$ then $q_n/q_{n+1}< 1/a\le 1/2$ for all $n\ge N$.

The significance of rational convergents is that they provide extremely good approximations to $\alpha$. We will make use of the following strong approximation property.

Lemma 2.2

(Theorem 182 of Hardy and Wright [5]) Let $\alpha$ be an irrational number. Then for all rational convergents $p_n/q_n$ of $\alpha$ and all rational numbers p / q with $1\le q<q_{n+1}$

$$\begin{aligned} |q_n\alpha -p_n|\le |q\alpha -p| \end{aligned}$$

with equality if and only if $p/q=p_n/q_n$.

We remark that the statement of Theorem 182 of Hardy and Wright [5] only gives this result for $q<q_n$. However, in the proof they show that if $q_{n-1}<q<q_n$ then $|q\alpha -p|>|q_{n-1}\alpha -p_{n-1}|$. This implies our statement by changing n to $n+1$.

The following estimate of the error in approximating $\alpha$ by $p_n/q_n$ will be crucial to our arguments below.

Proposition 2.3

(Dirichlet, Theorem 171 of Hardy and Wright [5]) Let $\alpha$ be an irrational number and let $p_n/q_n$ denote the rational convergents of $\alpha$. Then for all $n\ge 1$ we have:

$$\begin{aligned} \left| \alpha -\frac{p_n}{q_n}\right| \le \frac{1}{q_nq_{n+1}}. \end{aligned}$$

(9)

We also need a similar lower bound. This result follows from Theorem 163 and equation (10.7.4) of Hardy and Wright [5], see also Lemma 2.7 (ii) of Erlandsson and Zakeri [2]:

Lemma 2.4

Let $\alpha$ be an irrational number and let $p_n/q_n$ denote the rational convergents of $\alpha$. Then for all $n\ge 1$ we have:

$$\begin{aligned} \left| \alpha -\frac{p_n}{q_n}\right| > \frac{1}{2q_nq_{n+1}}. \end{aligned}$$

Our main application of Diophantine approximation will be to estimate the sine of small angles. We use the following elementary lemma.

Lemma 2.5

For all $0<x\le \pi /2$ we have

$$\begin{aligned} 2x/\pi \le \sin (x)<x. \end{aligned}$$

Thus we have:

Lemma 2.6

Let $\alpha$ be irrational and let $p_n/q_n$, with $n\in {{\mathbb {N}}}$, be its rational convergents. Then

$$\begin{aligned} \bigl |2\sin (\pi q_n\alpha )\bigr | < 2\pi /q_{n+1}. \end{aligned}$$

(10)

Proof

Multiplying the inequality (9) from Dirichlet’s theorem by $\pi q_n$, for $n\ge 1$ we have

$$\begin{aligned} \bigl |\pi q_n\alpha -\pi p_n\bigr |\le \frac{\pi }{q_{n+1}}\le \frac{\pi }{2}. \end{aligned}$$

Since $\sin (x)$ is monotone increasing for $0\le x\le \pi /2$ we see that

$$\begin{aligned} \bigl |2\sin (\pi q_n\alpha )\bigr | =2\sin \bigl |\pi q_n\alpha -\pi p_n\bigr | \le 2\sin (\pi /q_{n+1}) < 2\pi /q_{n+1}. \end{aligned}$$

The last inequality follows from Lemma 2.6. $\square$

Since (8) implies $\alpha -p_{2m-1}/q_{2m-1}<0<\alpha -p_{2m}/q_{2m}$, we can get information about the sign of $\sin (\pi q_n\alpha )$. Combining this information with Lemma 2.6 yields:

$$\begin{aligned} -2\pi /q_{2m}<2\sin (\pi q_{2m-1}\alpha )<0<2\sin (\pi q_{2m}\alpha )<2\pi /q_{2m+1}. \end{aligned}$$

We also want to find lower bounds on the sine of small angles.

Lemma 2.7

Let $\alpha$ be irrational and let $p_n/q_n$, with $n\in {{\mathbb {N}}}$, be its rational convergents. Then

$$\begin{aligned} \bigl |2\sin (\pi q_n\alpha )\bigr | \ge 1/q_{n+1}. \end{aligned}$$

(11)

Proof

Using a similar argument to Lemma 2.6 only using the lower bound for $|\alpha -p_n/q_n|$ from Lemma 2.4 gives:

$$\begin{aligned} |\sin (\pi q_n\alpha )|>\sin (\pi /2q_{n+1})>(2/\pi )\cdot (\pi /2q_{n+1})=1/q_{n+1}. \end{aligned}$$

$\square$

A rational number is said to be a Diophantine number of exponent $\nu \ge 2$ if there exists a constant $K=K(\alpha )>0$ only depending on $\alpha$ so that

$$\begin{aligned} \left| \alpha -\frac{p}{q}\right| >\frac{K}{q^\nu } \end{aligned}$$

(12)

for every rational p / q (where without loss of generality we take $q>0$). Since (12) holds for the case where $q=1$, which is $|\alpha -p|>K$ for all $p\in {{\mathbb {Z}}}$, we see that $K<1/2$.

We define ${{\mathcal {D}}}_\nu$ to be the set of Diophantine numbers of exponent $\nu$. A theorem of Liouville (Theorem 191 of Hardy and Wright [5]) says that when $\alpha$ is an algebraic number $\alpha$ is Diophantine and the exponent $\nu$ may be taken to be the degree of its minimum polynomial. For example, if $\alpha$ is a quadratic irrational then there exists an integer $a\ge 1$ so that $a_n\le a$ for all $n\ge 1$. It is then not hard to show (see Theorem 188 of Hardy and Wright [5]) that for any rational p / q we have

$$\begin{aligned} \left| \alpha -\frac{p}{q}\right| >\frac{1}{(a+2)^3q^2}. \end{aligned}$$

Lemma 2.8

Let $\alpha$ be Diophantine of exponent $\nu \ge 2$ and let K be the constant from Eq. (12). Then for every $q\in {{\mathbb {N}}}$

$$\begin{aligned} |2\sin (\pi q \alpha )|>\frac{4K}{q^{\nu -1}}. \end{aligned}$$

Proof

From Eq. (12) we see that for all rationals p / q

$$\begin{aligned} |\pi q \alpha -\pi p|>\frac{\pi K}{q^{\nu -1}}. \end{aligned}$$

Since this is valid for all $p\in {{\mathbb {Z}}}$ we may assume the left hand side is at most $\pi /2$. Using the monotonicity of the sine function on the interval $(0,\pi /2]$ and Lemma 2.6, we have

$$\begin{aligned} |2\sin (\pi q\alpha )|=2\sin |\pi q\alpha -\pi p| > 2\sin \left( \frac{\pi K}{q^{\nu -1}}\right) \ge 2\cdot \frac{2}{\pi }\cdot \frac{\pi K}{q^{\nu -1}} =\frac{4K}{q^{\nu -1}}. \end{aligned}$$

$\square$

3 Real hyperbolic 4-space

3.1 Sub-horospherical regions

We use the upper half space model of real hyperbolic 4-space $\mathbf{H}^4_{{\mathbb {R}}}$ and we give it cylindrical polar coordinates $(r,\theta ,v,u)$, which correspond to $\bigl (r\cos (\theta ),r\sin (\theta ),v,u\bigr )\in {{\mathbb {R}}}^4$. In these coordinates:

$$\begin{aligned} \mathbf{H}^4_{{\mathbb {R}}}=\Bigl \{ (r,\theta ,v,u)\ :\ u>0\Bigr \}. \end{aligned}$$

The (Poincaré) hyperbolic distance $\rho \bigl (x_1,x_2)$ between points $x_1=(r_1,\theta _1,v_1,u_1)$ and $x_2=(r_2,\theta _2,v_2,u_2)$ in $\mathbf{H}^4_{{\mathbb {R}}}$ is given by

$$\begin{aligned} \cosh ^2\left( \frac{\rho (x_1,x_2)}{2}\right) =\frac{\bigl |r_1e^{i\theta _1}-r_2e^{i\theta _2}\bigr |^2+(v_1-v_2)^2+(u_1+u_2)^2}{4u_1u_2}. \end{aligned}$$

(13)

For $u_0>0$ the horosphere $H_{u_0}$ and horoball $B_{u_0}$ based at $\infty$ of height $u_0$ are defined by:

$$\begin{aligned} H_{u_0}=\Bigl \{(r,\theta ,v,u)\in \mathbf{H}^4_{{\mathbb {R}}}\ :\ u=u_0\Bigr \},\quad B_{u_0}=\Bigl \{(r,\theta ,v,u)\in \mathbf{H}^4_{{\mathbb {R}}}\ :\ u>u_0\Bigr \}. \end{aligned}$$

Let $f(r,\theta ,v)$ be a positive function bounded away from 0. Then the sub-horospherical region with boundary function f is the subset of $\mathbf{H}^4_{{\mathbb {C}}}$ given by

$$\begin{aligned} \Bigl \{(r,\theta ,v,u)\in \mathbf{H}^4_{{\mathbb {R}}}\ :\ u>f(r,\theta ,v)\Bigr \}. \end{aligned}$$

Let $A=A_{\alpha ,t}:\mathbf{H}^4_{{\mathbb {R}}}\longrightarrow \mathbf{H}^4_{{\mathbb {R}}}$ be the screw parabolic isometry of $\mathbf{H}^4_{{\mathbb {R}}}$ defined by (1), that is:

$$\begin{aligned} A=A_{\alpha ,t}:(r,\theta ,v,u)\longmapsto (r,\theta +2\pi \alpha ,v+t,u) \end{aligned}$$

Then for any $q\in {{\mathbb {Z}}}$ the qth power of A is

$$\begin{aligned} A^q:(r,\theta ,v,u)\longmapsto (r,\theta +2\pi q\alpha ,v+qt,u) \end{aligned}$$

(14)

In what follows we will be especially interested in the case where $\alpha$ is irrational.

Let $\Gamma$ be a discrete subgroup of $\mathrm{Isom}(\mathbf{H}^4_{{\mathbb {C}}})$ and write $\Gamma _\infty$ for the stabiliser of $\infty$ in $\Gamma$. Using Theorem 2.5 of Erlandsson and Zakeri [2], if $\Gamma _\infty$ contains a screw parabolic map $A_{\alpha ,t}$ whose rotation angle $2\pi \alpha$ is an irrational multiple of $\pi$ then $\Gamma _\infty$ is (possibly a finite extension of) an infinite cyclic group. The finite extension arises because there may be finite order elliptic elements that pointwise fix the rotation axis of $A_{\alpha ,t}$. These elliptic elements have no effect on precisely invariant regions far from the rotation axis. Thus, without loss of generality, we may assume $\Gamma _\infty$ is infinite cyclic with generator $A=A_{\alpha ,t}$. Also, swapping to $A^{-1}$ if necessary, we assume $t>0$.

A set V is said to be precisely invariant under $\Gamma _\infty$ in $\Gamma$ if $A(V)=V$ for all $A\in \Gamma _\infty$ and $B(V)\cap V=\emptyset$ for all $B\in \Gamma -\Gamma _\infty$. For any discrete group $\Gamma$ with $\Gamma _\infty =\langle A_{\alpha ,t}\rangle$, our aim is to construct a sub-horospherical region depending only on $\alpha$ and t that is precisely invariant under $\Gamma _\infty$ in $\Gamma$. To that end, the we will consider sub-horospherical regions $V_f$ whose boundary functions $f_{\alpha ,t}$ depend only on r and not on $\theta$ or v. If $V_f$ is a precisely invariant sub-horosherical region with boundary function $f_{\alpha ,t}(r)$ and if $g_{\alpha ,t}(r)$ is a function of $r\ge 0$ depending on $\alpha$ and t for which $g_{\alpha ,t}(r)\ge f_{\alpha ,t}(r)$ for all $r\ge 0$ then the sub-horospherical region $V_g$ with boundary function $g_{\alpha ,t}$ is contained in $V_f$. Thus $B(V_g)\cap V_g=\emptyset$ for all $B\in \Gamma -\Gamma _\infty$. Since g is independent of $\alpha$ and t then $A^q_{\alpha ,t}(V_g)=V_g$ for all $q\in {{\mathbb {Z}}}$ and so $V_g$ is also precisely invariant under $\Gamma _\infty$ in $\Gamma$.

For any $k>0$ the Euclidean dilation $D_k:\mathbf{H}^4_{{\mathbb {R}}}\longrightarrow \mathbf{H}^4_{{\mathbb {R}}}$ given by $D_k(r,\theta ,v,u)=(kr,\theta ,kv,ku)$ is a loxodromic isometry of $\mathbf{H}^4_{{\mathbb {R}}}$. We want to give formulae that are invariant under such dilations. Therefore, we want to find formulae that are homogeneous in r, v and u. In particular, $f_{\alpha ,t}(r)$ should be r times a function of r / t. We note that Erlandsson and Zakeri normalise $t=1$ and so produce inhomogeneous formulae. These can be made homogeneous by inserting suitable powers of t according to this recipe.

3.2 The Margulis region and the Erlandsson–Zakeri boundary function

A celebrated result of Margulis says (in the case of $\mathbf{H}^4_{{\mathbb {R}}}$) the following. There is a universal constant $\varepsilon >0$ so that for any discrete group $\Gamma$ of isometries of $\mathbf{H}^4_{{\mathbb {R}}}$ and any $x\in \mathbf{H}^4_{{\mathbb {R}}}$ if

$$\begin{aligned} \Sigma _{\varepsilon ,x}=\Bigl \{A\in \Gamma \ :\ \rho \bigl (A(x),x\bigr )<\varepsilon \Bigr \} \end{aligned}$$

then the subgroup $\Gamma _{\varepsilon ,x}$ of $\Gamma$ generated by the the set $\Sigma _{\varepsilon ,x}$ contains a nilpotent subgroup of finite index. Of course, for many points $x\in \mathbf{H}^4_{{\mathbb {R}}}$ the group $\Gamma _{\varepsilon ,x}$ is trivial (or finite). Let M be the orbifold $\Gamma \backslash \mathbf{H}^4_{{\mathbb {R}}}$ and $\Pi :\mathbf{H}^4_{{\mathbb {R}}}\longrightarrow M=\Gamma \backslash \mathbf{H}^4_{{\mathbb {R}}}$ the canonical projection. The $\varepsilon$ -thin part $M_{\varepsilon }$ of the orbifold M is the set of points $\Pi (x)\in M$ where $\Gamma _{\varepsilon ,x}$ is infinite. Geometrically this means that there is a homotopically non-trivial path from $\Pi (x)$ to itself with length at most $\varepsilon$. Margulis’s theorem says that, again for this universal constant $\varepsilon$, the $\varepsilon$-thin part $M_{\varepsilon }$ of M is the union of Margulis tubes around short geodesics or Margulis cusps around parabolic fixed points.

We will be interested in the case of Margulis cusps where the group $\Gamma _{\varepsilon ,x}$ contains a screw-parabolic map $A=A_{\alpha ,t}$ given by (1) with $\alpha$ irrational and $t>0$. In this case the parabolic fixed point is $\infty$ and $\Gamma _{\varepsilon ,x}=\Gamma _\infty$ is the cyclic group generated by A. Hence the Margulis cusp is $\Gamma _\infty \backslash T_{\alpha ,t}$ where

$$\begin{aligned} T_{\alpha ,t}=\Bigl \{x=(r,\theta ,v,u)\ :\ \rho \bigl (A^q(x),x\bigr )<\varepsilon \hbox { for some }q\in {{\mathbb {Z}}}\Bigr \}. \end{aligned}$$

Using Eq. (13) we see that the hyperbolic translation length of $A^q$ at the point $x=(r,\theta ,v,u)$ is given by

$$\begin{aligned} \sinh \left( \frac{\rho \bigl (A^q(x),x\bigr )}{2}\right) =\frac{\sqrt{4\sin ^2(\pi q\alpha )r^2+q^2t^2}}{2u}. \end{aligned}$$

(15)

Hence, if $A^q$ translates by a hyperbolic distance less than $\varepsilon$ then

$$\begin{aligned} u>u_{q\alpha ,qt}=\frac{\sqrt{4\sin ^2(\pi q\alpha )r^2+q^2t^2}}{2\sinh (\varepsilon /2)}. \end{aligned}$$

We write $c(\varepsilon )=1/\bigl (2\sinh (\varepsilon /2)\bigr )$. Note that since A is an isometry, the translation lengths of $A^q$ and $A^{-q}$ are the same; which may also be seen by sending q to $-q$ in the above formula. Thus, for a given $q\in {{\mathbb {Z}}}$, the set on which $A^q$ and $A^{-q}$ have translation length less that $\varepsilon$ is

$$\begin{aligned} U_{q\alpha ,qt}=\left\{ (r,\theta ,v,u)\in \mathbf{H}^4_{{\mathbb {R}}}\ :\ u>c(\varepsilon )\sqrt{4\sin ^2(\pi q\alpha )r^2+q^2t^2}\right\} . \end{aligned}$$

The set on which there exists a non-zero integer q so that $A^q$ has translation length less that $\varepsilon$ is

$$\begin{aligned} T_{\alpha ,t}=\bigcup _{q\ge 1}U_{q\alpha ,qt} =\left\{ (r,\theta ,v,u)\in \mathbf{H}^4_{{\mathbb {R}}}\ :\ u>c(\varepsilon )\inf _{q\ge 1}\sqrt{4\sin ^2(\pi q\alpha )r^2+q^2t^2}\right\} . \end{aligned}$$

This sub-horospherical region is sent by the projection map $\Pi$ to the the Margulis cusp around $\infty$ associated to $\varepsilon$. Thus, it is enough to study the boundary function ${{\mathcal {B}}}_{\alpha ,t}(R)$ associated to this region; see equation (10) of Erlandsson and Zakeri:

$$\begin{aligned} {{\mathcal {B}}}_{\alpha ,t}(r) =c(\varepsilon )\inf _{q\ge 1}\sqrt{4\sin ^2(\pi q\alpha )r^2+q^2t^2}. \end{aligned}$$

Following Susskind [11], Erlandsson and Zakeri show that if $\Gamma$ is any group of isometries of $\mathbf{H}^4_{{\mathbb {R}}}$ containing $A=A_{\alpha ,t}$ then $T_{\alpha ,t}$ is precisely invariant under $\Gamma _\infty$ in $\Gamma$.

For each value of $r\ge 0$ the infimum of ${{\mathcal {B}}}_{\alpha ,t}(r)$ is attained for some value of q. Erlandsson and Zakeri give a detailed and beautiful analysis of how the value of q where the minimum is attained varies with q. Their starting point is the following lemma, which gives the link to continued fractions:

Lemma 3.1

(Susskind [11]; Lemma 3.1 of Erlandsson and Zakeri [2]) If $q\ge 1$ attains the infimum in ${{\mathcal {B}}}_{\alpha ,t}(r)$ for some $r\ge 0$ then $q=q_n$ is the denominator of some rational convergent $p_n/q_n$ of $\alpha$.

3.3 An upper bound for the boundary function ${{\mathcal {B}}}_{\alpha ,t}(x)$

The problem with the results in [2] is that the exact pattern of which rational convergents correspond to $q=q_n$ attaining the minimum for some r is very complicated and depends heavily on the arithmetic properties of $\alpha$. It is then hard to extract geometrical information. In contrast, we seek to give a universal upper bound on ${{\mathcal {B}}}_{\alpha ,t}(r)$ and so produce a smaller sub-horospherical region, but one that works for all irrational $\alpha$. As in Erlandsson and Zakeri’s paper [2], we concentrate on what happens when $r>r_0>0$ for some $r_0$ (which depends on $\alpha$). One can always fill in the solid cylinder where $r\le r_0$ with the function corresponding to a particular value of q, say $q=1$. Since our focus is on the behaviour of ${{\mathcal {B}}}_{\alpha ,t}(r)$ for large r, we do not go into details of this process here.

The following simple lemma is the main tool we use to produce our estimates.

Lemma 3.2

Let $t>0$. Let $\alpha$ be irrational and let $p_n/q_n$, with $n\in {{\mathbb {N}}}$, be its rational convergents. Then for all r with

$$\begin{aligned} \frac{q_n^2t}{2\pi }\le r\le \frac{q_{n+1}^2t}{2\pi } \end{aligned}$$

we have

$$\begin{aligned} 4\sin ^2(\pi q_n\alpha )r^2+q_n^2t^2 < \left( 1+\frac{q_n^2}{q_{n+1}^2}\right) 2\pi tr. \end{aligned}$$

Proof

Using Lemma 2.6 we have

$$\begin{aligned} 4\sin ^2(\pi q_n\alpha )r^2+q_n^2t^2< & {} \frac{4\pi ^2 r^2}{q_{n+1}^2}+q_n^2t^2 \\= & {} \left( 1+\frac{q_n^2}{q_{n+1}^2}\right) 2\pi tr +\left( \frac{2\pi r}{q_{n+1}^2}-t\right) \left( 2\pi r-q_n^2t\right) \\\le & {} \left( 1+\frac{q_n^2}{q_{n+1}^2}\right) 2\pi tr. \end{aligned}$$

The last inequality is a consequence of $(2\pi r/q_{n+1}^2-t)\le 0\le (2\pi r-q_n^2t)$ for the given range of r. $\square$

Fig. 1

The graphs of the function from Proposition 3.3 (green) and the functions from [2] (red) in the case of $\alpha =\bigl (\sqrt{5}+1\bigr )/2=[1;1,1,1,\ldots ]$. In this case we take $q_N=2, \lambda _N=q_N/q_{N+1}=2/3$ and $t=1$. (Compare Figure 2 of [2]). (Color figure online)

Therefore we have:

Proposition 3.3

Given $N\in {{\mathbb {N}}}$, suppose that $\lambda _N\in (0,1]$ is a constant for which $q_n/q_{n+1}\le \lambda _N$ for all $n\ge N$. Then for all $r\ge q_N^2t/2\pi$ we have

$$\begin{aligned} {{\mathcal {B}}}_{\alpha ,t}(r)< c(\varepsilon )\sqrt{\left( 1+\lambda _N^2\right) 2\pi t}\sqrt{r}. \end{aligned}$$

In particular, taking $N=1$ and $\lambda _1=1$, for all $r\ge q_1^2t/2\pi$ we have

$$\begin{aligned} {{\mathcal {B}}}_{\alpha ,t}(r)< c(\varepsilon )\sqrt{4\pi t}\sqrt{r}. \end{aligned}$$

Proof

Let $r\ge q_N^2t/2\pi$. Since $\{q_n\}$ is a strictly increasing sequence of positive integers, then there is an $n\ge N$ for which $q_n^2t/2\pi \le r\le q_{n+1}^2t/2\pi$. Therefore, using Lemma 3.2, we have:

$$\begin{aligned} {{\mathcal {B}}}_{\alpha ,t}(r)= & {} c(\varepsilon )\,\inf _{q\ge 1}\sqrt{4\sin ^2(\pi q\alpha )r^2+q^2t} \\\le & {} c(\varepsilon )\sqrt{4\sin ^2(\pi q_n\alpha )r^2+q_n^2t} \\< & {} c(\varepsilon )\sqrt{\left( 1+\frac{q_n^2}{q_{n+1}^2}\right) 2\pi t} \sqrt{r} \\\le & {} c(\varepsilon )\sqrt{(1+\lambda _N^2)2\pi t}\sqrt{r}. \end{aligned}$$

This is the desired result. $\square$

The only way the bound in Proposition 3.3 depends on $\alpha$ is through the constant $\lambda _N$, which may always be taken to be $\lambda _N=1$. Given arithmetical information about $\alpha$ we can often give a value of $\lambda _N$ strictly smaller than 1. Here are four typical examples.

• (1) Suppose $\alpha =[a_0;a_1,a_2,\ldots ]$ with $a_n\ge a\ge 2$ for all $n\ge N$. From Lemma 2.1 we have $q_n/q_{n+1}<1/a$ and so then we can take $\lambda _N=1/a$.

• (2) If $\alpha =(\sqrt{5}+1)/2=[1;1,1,1,\ldots ]$ then $q_0=q_1=1$ and $q_{n+1}=q_n+q_{n-1}$. It is easy to see that for all $m\ge 1$:

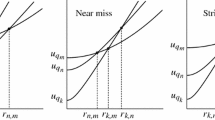
  $$\begin{aligned} \frac{1}{2}=\frac{q_1}{q_2}\le \frac{q_{2m-1}}{q_{2m}}<\frac{\sqrt{5}-1}{2} <\frac{q_{2m}}{q_{2m+1}}\le \frac{q_2}{q_3}=\frac{2}{3}. \end{aligned}$$

  Thus, for all $n\ge 2$ we have $q_n/q_{n+1}\le q_2/q_3=2/3$. So we take $\lambda _2=2/3$. We use this in Fig. 1. Note that we could decrease $\lambda$ to $q_{2M}/q_{2M+1}$ by only considering $n\ge N=2M$ and hence we can take $\lambda _{2M}$ arbitrarily close to $\bigl (\sqrt{5}-1\bigr )/2$.

• (3) On the other hand, if $\alpha =\bigl (\sqrt{21}+3\bigr )/6=[1;3,1,3,\ldots ]$ then $q_0=1, q_1=3, q_{2m}=q_{2m-1}+q_{2m-2}$ and $q_{2m+1}=3q_{2m}+q_{2m-1}$. We can then check that for all $m\ge 0$:

  $$\begin{aligned} \frac{\sqrt{21}-3}{6}<\frac{q_{2m}}{q_{2m+1}}\le \frac{q_0}{q_1}=\frac{1}{3}<\frac{3}{4}=\frac{q_1}{q_2}\le \frac{q_{2m+1}}{q_{2m+2}}<\frac{\sqrt{21}-3}{2}. \end{aligned}$$

  Therefore, we take $\lambda _N=\bigl (\sqrt{21}-3\bigr )/2$. We use this in Fig. 2. In this case, $q_{2m+1}/q_{2m+2}$ tends to $\bigl (\sqrt{21}-3\bigr )/2$ as m tends to infinity, so there is no possibility of decreasing $\lambda _N$.

• (4) It is not always possible to improve $\lambda _N= 1$. For example, consider $\alpha =[a_0;a_1,a_2,\ldots ]$ where $a_{2m}=m$ and $a_{2m+1}=1$. Then

  $$\begin{aligned} q_{2m}=mq_{2m-1}+q_{2m-2}>mq_{2m-1},\quad q_{2m+1}=q_{2m}+q_{2m-1}<q_{2m}+q_{2m}/m. \end{aligned}$$

  Thus $q_{2m}/q_{2m+1}>m/(m+1)$ and so the minimum possible value of $\lambda _N$ is 1.

Fig. 2

The graphs of the function from Proposition 3.3 (green) and the functions from [2] (red) in the case of $\alpha =\bigl (\sqrt{21}+3\bigr )/6=[1;3,1,3,\ldots ]$. In this case we take $q_N=4, \lambda _N=\bigl (\sqrt{21}-3\bigr )/2$ and $t=1$. (Compare Figure 3 of [2]). (Color figure online)

3.4 A lower bound on the boundary function ${{\mathcal {B}}}_{\alpha ,t}(r)$

We give a lower bound on ${{\mathcal {B}}}_{\alpha ,t}(r)$ when $\alpha$ is Diophantine of exponent $\nu \ge 2$. In particular, this holds for algebraic numbers $\alpha$ with minimum polynomial of degree $\nu$. Our lower bound has better asymptotic behaviour than the lower bound from [2] whenever the Diophantine exponent $\nu$ is greater than 2.

Lemma 3.4

Let $t>0$ and let $\alpha$ be Diophantine of exponent $\nu \ge 2$ with K the constant from (12). Then for all $q\in {{\mathbb {N}}}$ and all $r>0$:

$$\begin{aligned} 4\sin ^2(\pi q\alpha )r^2+q^2t^2 >\frac{\bigl (4K\bigr )^{2/\nu }\nu t^{2(\nu -1)/\nu }}{(\nu -1)^{(\nu -1)/\nu }} \ r^{2/\nu }. \end{aligned}$$

Proof

Using Lemma 2.8, for all $q\in {{\mathbb {N}}}$, we have

$$\begin{aligned} 4\sin ^2(\pi q\alpha )r^2+q^2t^2> \frac{16K^2r^2}{q^{2\nu -2}}+q^2t^2. \end{aligned}$$

The weighted arithmetic-geometric mean inequality (equation (2.5.2) of Hardy et al. [6]) states that if $a_i>0$ and $p_i>0$ with $p_1+p_2=1$ then

$$\begin{aligned} p_1a_1+p_2a_2\ge a_1^{p_1}a_2^{p_2}. \end{aligned}$$

We choose the weights $p_1$ and $p_2$ so that the powers of q cancel. That is

$$\begin{aligned} p_1=\frac{1}{\nu },\quad p_2=\frac{\nu -1}{\nu },\quad a_1=\frac{16K^2\nu r^2}{q^{2\nu -2}}, \quad a_2=\frac{q^2t^2\nu }{\nu -1}. \end{aligned}$$

Then

$$\begin{aligned} \frac{16K^2r^2}{q^{2\nu -2}}+q^2t^2= & {} \left( \frac{16K^2\nu r^2}{q^{2\nu -2}}\right) \frac{1}{\nu } +\left( \frac{q^2t^2\nu }{\nu -1}\right) \frac{\nu -1}{\nu } \\\ge & {} \left( \frac{16K^2\nu r^2}{q^{2(\nu -1)}}\right) ^{1/\nu }\cdot \left( \frac{q^2t^2\nu }{\nu -1}\right) ^{(\nu -1)/\nu } \\= & {} \frac{(4K)^{2/\nu }\nu t^{2(\nu -1)/\nu }}{(\nu -1)^{(\nu -1)/\nu }} \,r^{2/\nu }. \end{aligned}$$

This gives the result. $\square$

Using the definition of ${{\mathcal {B}}}_{\alpha ,t}(r)$ the following proposition follows directly from Lemma 3.4.

Proposition 3.5

Let $t>0$ and let $\alpha$ be Diophantine of exponent $\nu \ge 2$ with K be the constant from (12). Then

$$\begin{aligned} {{\mathcal {B}}}_{\alpha ,t}(r) >\frac{c(\varepsilon )(4K)^{1/\nu }\nu ^{1/2}t^{(\nu -1)/\nu }}{(\nu -1)^{(\nu -1)/2\nu }}\ r^{1/\nu }. \end{aligned}$$

In particular, if $\nu =2$ then

$$\begin{aligned} {{\mathcal {B}}}_{\alpha ,t}(r) >c(\varepsilon )\sqrt{8Kt}\ \sqrt{r}. \end{aligned}$$

3.5 An example

The following example is inspired by the work of Ohtake [9]. He constructed discrete groups generated by a screw parabolic map A fixing $\infty$ and an involution B not fixing $\infty$ with isometric sphere S of arbitrarily large radius R. To do so, the distance r of the centre of S from the axis of A must be large as well. We quantify the relationship between R and r in terms of the Diophantine exponent $\nu$ of the rotation angle of A.

Proposition 3.6

Suppose that the screw parabolic map $A=A_{\alpha ,t}$ has the form (1). Let $r_0>0$ be any positive constant. Then there exists a discrete group $\Gamma$ for which $\Gamma _\infty =\langle A\rangle$ and a point $(r,\theta ,v,u)\in \mathbf{H}^2_{{\mathbb {R}}}$ with $r>r_0$ and $u>\sqrt{t/2}\sqrt{r}$ that cannot lie in any precisely invariant sub-horospherical region for $\Gamma$.

Proof

Consider the (Euclidean) hemisphere S of radius R whose centre, written in cylindrical polar coordinates, is $\bigl (r,\theta ,v,0\bigr )\in \partial \mathbf{H}^4_{{\mathbb {R}}}$. For $q\in {{\mathbb {Z}}}$, the image of S under $A^q$ is the hemisphere $A^q(S)$ with radius R and centre $\bigl (r,\theta +2\pi q\alpha ,v+qt,0\bigr )$. The distance between the centres of S and $A^q(S)$ is

$$\begin{aligned} \sqrt{4\sin ^2(\pi q\alpha )r^2+q^2t^2}. \end{aligned}$$

If this distance is at least 2R then S and $A^q(S)$ are disjoint or tangent. That is, we want:

$$\begin{aligned} 4R^2\le 4\sin ^2(\pi q\alpha )r^2+q^2t^2. \end{aligned}$$

Let $p_n/q_n$ be a rational convergent of $\alpha$. Choose $r_n$ and $R_n$ so that

$$\begin{aligned} R_n=\frac{q_{n+1}t}{2},\quad r_n=\frac{q_{n+1}t}{2|\sin (\pi q_n\alpha )|} =\frac{R_n}{|\sin (\pi q_n\alpha )|}. \end{aligned}$$

(16)

Let $S_n$ be the hemisphere with centre $(r_n,0,0,0)\in \partial \mathbf{H}^4_{{\mathbb {R}}}$ and radius $R_n$. Note that

$$\begin{aligned} r_n=\frac{q_{n+1} t}{2|\sin (\pi q_n\alpha )|}>\frac{q_{n+1}^2 t}{2\pi } \end{aligned}$$

and so given $r_0>0$ we can find n so that $q_{n+1}^2t/2\pi >r_0$ and hence $r_n>r_0$.

We claim that $S_n$ is disjoint from $A^q(S_n)$ for all $q\in {{\mathbb {Z}}}-\{0\}$:

• (1) For all $q\in {{\mathbb {Z}}}$ with $q\ge q_{n+1}$ we have

  $$\begin{aligned} 4\sin ^2(\pi q\alpha )r_n^2+q^2t^2\ge q^2t^2 \ge q_{n+1}^2t^2= 4R_n^2. \end{aligned}$$

  Therefore $S_n$ is disjoint from $A^{\pm q}(S_n)$.

• (2) For all $q\in {{\mathbb {Z}}}$ with $1\le q<q_{n+1}$ and for all p, Lemma 2.2 implies

  $$\begin{aligned} |q_n\alpha -p_n|\le |q\alpha -p|. \end{aligned}$$

  We may assume that the right hand side is at most 1 / 2 and so

  $$\begin{aligned} |\sin (\pi q_n\alpha )|=\sin |\pi q_n\alpha -\pi p_n|\le \sin |\pi q\alpha -\pi p|=|\sin (\pi q\alpha )|. \end{aligned}$$

  Therefore

  $$\begin{aligned} 4\sin ^2(\pi q\alpha )r_n^2+q^2t^2\ge 4\sin ^2(\pi q\alpha )r_n^2\ge 4\sin ^2(\pi q_n\alpha )r_n^2=4R_n^2. \end{aligned}$$

  Therefore $S_n$ is disjoint from $A^{\pm q}(S_n)$.

Let $B_n$ be an involution fixing (at least) the point $z_n=(r_n,0,0,R_n)\in S_n$ and mapping the exterior of $S_n$ to its interior and vice versa. Since $S_n$ is disjoint from $A^q(S_n)$ for all $q\in {{\mathbb {Z}}}-\{0\}$, a combination theorem argument shows that the group $\Gamma _n$ generated by A and $B_n$ is discrete. The point $z_n=(r_n,0,0,R_n)$ cannot lie in any precisely invariant sub-horospherical region for $\Gamma _n$ since it is fixed by $B_n$.

The point $z_n=(r_n,0,0,R_n)$ lies on the horosphere of height $u=R_n$ satisfying:

$$\begin{aligned} u^2= & {} R_n^2 \\= & {} |\sin (\pi q_n\alpha )|r_n\cdot q_{n+1}t/2 \\\ge & {} \frac{r_n}{q_{n+1}}\cdot \frac{q_{n+1} t}{2} \\= & {} \frac{r_nt}{2}. \end{aligned}$$

The inequality follows using Lemma 2.7. This completes the proof. $\square$

3.6 An explicit bound using Waterman’s theorem

In [12] Waterman gives a version of Shimizu’s lemma for real hyperbolic space of dimension at least 4. He uses $2\times 2$ matrices over a Clifford algebra. For $\mathbf{H}^4_{{\mathbb {R}}}$ these are matrices over the quaternions. In Waterman’s language, the point $x\in \mathbf{H}^4_{{\mathbb {R}}}$ with cylindrical polar coordinates $(r,\theta ,v,u)$ corresponds to the quaternion $v+r\cos (\theta )i+r\sin (\theta )j+uk$ and the map A given by (1) is

$$\begin{aligned} A_{{\mathbb {H}}}=\left( \begin{matrix} \lambda &{} \lambda t \\ 0 &{} \lambda \end{matrix}\right) \end{aligned}$$

where $\lambda =\cos (\pi \alpha )+k\sin (\pi \alpha )$ (compare page 101 of Waterman [12]). Waterman denotes the imaginary part of $\lambda$ by $\lambda _C$. Thus, in our case, $\lambda _C=k\sin (\pi \alpha )$ and $|\lambda _C|=|\sin (\pi \alpha )|$. In our language, Waterman’s result says:

Theorem 3.7

(Theorem 8 of Waterman [12]) Let $\Gamma$ be a discrete subgroup of $\mathrm{Isom}(\mathbf{H}^4_{{\mathbb {R}}})$ containing a screw-parabolic map A written in the form (1). Suppose that $4|\sin (\pi \alpha )|<1/2$. Let B be any element of $\Gamma$ not fixing $\infty$. Suppose that the isometric spheres of B and $B^{-1}$ have radius $R_B$ and centres $B^{-1}(\infty )=(r_+,\theta _+,v_+,0)$ and $B(\infty )=(r_-,\theta _-,v_-,0)$ respectively. Then

$$\begin{aligned} R_B^2\le \frac{2\sqrt{4\sin ^2(\pi \alpha )r_+^2+t^2}}{1+\sqrt{1-8|\sin (\pi \alpha )|}}\cdot \frac{2\sqrt{4\sin ^2(\pi \alpha )r_-^2+t^2}}{1+\sqrt{1-8|\sin (\pi \alpha )|}}. \end{aligned}$$

We now convert Waterman’s theorem into a statement about a precisely invariant sub-horospherical region (compare with Section 2 of Erlandsson and Zakeri [3]). For $0<X<1/2$ define

$$\begin{aligned} \Delta _{{\mathbb {R}}}(X)=\frac{\bigl (1+\sqrt{1-2X}\bigr )^2-X^2}{4}. \end{aligned}$$

(17)

Note that for $\Delta _{{\mathbb {R}}}$ is a decreasing function for $0<X<1/2$

Proposition 3.8

Let $\Gamma$ be a discrete subgroup of $\mathrm{Isom}(\mathbf{H}^4_{{\mathbb {R}}})$ containing a screw-parabolic map A written in the form (1). Let $\Delta _{{\mathbb {R}}}$ be defined by (17). Suppose that $4|\sin (\pi \alpha )|<1/2$. Define

$$\begin{aligned} {\widehat{U}}_{\alpha ,t}=\left\{ (r,\theta ,v,u)\in \mathbf{H}^4_{{\mathbb {R}}}\ :\ u^2>\frac{4\sin ^2(\pi \alpha )r^2+t^2}{\Delta _{{\mathbb {R}}}\bigl (4|\sin (\pi \alpha )|\bigr )}. \right\} \end{aligned}$$

(18)

Then ${\widehat{U}}_{\alpha ,t}$ is precisely invariant under $\Gamma _\infty$ in $\Gamma$.

Proof

The centres $B^{-1}(\infty )=(r_+,\theta _+,v_+,0)$ and $B(\infty )=(r_-,\theta _-,v_-,0)$ of the isometric spheres of B and $B^{-1}$ may have very different values of $r_+$ and $r_-$. However, we want a radius that only depends on the r coordinate of the centre of the sphere. An elementary geometrical argument shows that, for any $R>0$, the map B sends the exterior of a sphere of radius R centred at $B^{-1}(\infty )$ to the interior of a sphere of radius $R_B^2/R$ centred at $B(\infty )$. Therefore, we define the function $\Phi _{\alpha ,t}(r)$ by

$$\begin{aligned} \Phi _{\alpha ,t}(r) =\frac{2\sqrt{4\sin ^2(\pi \alpha )r^2+t^2}}{1+\sqrt{1-8|\sin (\pi \alpha )|}}. \end{aligned}$$

Then Theorem 3.7 says that

$$\begin{aligned} R_B^2\le \Phi _{\alpha ,t}(r_+)\Phi _{\alpha ,t}(r_-). \end{aligned}$$

Thus, B sends the exterior of a sphere $S_+$ of radius $R_+=\Phi _{\alpha ,t}(r_+)$ centred at $B^{-1}(\infty )$ to the interior of a sphere of radius $R_B^2/R_+=R_B^2/\Phi _{\alpha ,t}(r_+)$ centred at $B(\infty )$. By Waterman’s theorem,

$$\begin{aligned} R_B^2/\Phi _{\alpha ,t}(r_+)\le \Phi _{\alpha ,t}(r_-). \end{aligned}$$

Hence B sends the exterior of $S_+$ to the interior of a sphere $S_-$ of radius $R_-=\Phi _{\alpha ,t}(r_-)$ with centre $(r_-,\theta _-,v_-,0)$. Thus, it suffices to find a sub-horospherical region ${\widehat{U}}_{\alpha ,t}$ so that for all $(r_0,\theta _0,v_0,0)\in \partial \mathbf{H}^4_{{\mathbb {R}}}-\{\infty \}$, the region ${\widehat{U}}_{\alpha ,t}$ is contained in the exterior of the sphere $S_0$ with radius $R_0=\Phi _{\alpha ,t}(r_0)$ centred at $(r_0,\theta _0,v_0,0)$. Consider such a sphere $S_0$. Then for all $(r,\theta ,v,u)\in \mathbf{H}^4_{{\mathbb {R}}}$ on $S_0$ we have

$$\begin{aligned} R_0^2 = |re^{i\theta }-r_0e^{i\theta _0}|^2+(v-v_0)^2+u^2. \end{aligned}$$

Then

$$\begin{aligned} u^2= & {} R_0^2- |re^{i\theta }-r_0e^{i\theta _0}|^2-(v-v_0)^2 \\\le & {} R_0^2- |re^{i\theta }-r_0e^{i\theta _0}|^2 \\= & {} \frac{4\bigl (4\sin ^2(\pi \alpha )r_0^2+t^2\bigr )}{\bigl (1+\sqrt{1-8|\sin (\pi \alpha )|}\bigr )^2}- |re^{i\theta }-r_0e^{i\theta _0}|^2 \\\le & {} \frac{4\bigl (4\sin ^2(\pi \alpha )\bigl (r+|re^{i\theta }-r_0e^{i\theta _0}|\bigr )^2+t^2\bigr )}{\bigl (1+\sqrt{1-8|\sin (\pi \alpha )|}\bigr )^2}- |re^{i\theta }-r_0e^{i\theta _0}|^2. \end{aligned}$$

The last line is a quadratic polynomial in $|re^{i\theta }-r_0e^{i\theta _0}|$ with negative second derivative. A brief calculation shows that this expression takes its maximum value when

$$\begin{aligned} |re^{i\theta }-r_0e^{i\theta _0}|=\frac{16\sin ^2(\pi \alpha )r}{\bigl (1+\sqrt{1-8|\sin (\pi \alpha )|}\bigr )^2-16\sin ^2(\pi \alpha )}. \end{aligned}$$

Substituting this value back in, we find that

$$\begin{aligned} u^2\le & {} \frac{16\sin ^2(\pi \alpha )r^2}{\bigl (1+\sqrt{1-8|\sin (\pi \alpha )|}\bigr )^2-16\sin ^2(\pi \alpha )} +\frac{4t^2}{\bigl (1+\sqrt{1-8|\sin (\pi \alpha )|}\bigr )^2} \\\le & {} \frac{4\bigl (4\sin ^2(\pi \alpha )r^2+t^2\bigr )}{\bigl (1+\sqrt{1-8|\sin (\pi \alpha )|}\bigr )^2-16\sin ^2(\pi \alpha )} \\= & {} \frac{4\sin ^2(\pi \alpha )r^2+t^2}{\Delta _{{\mathbb {R}}}\bigl (4|\sin (\pi \alpha )|\bigr )}. \end{aligned}$$

Thus, the sphere $S_0$ with centre $(r_0,\theta _0,v_0,0)$ and radius $R_0=\Phi _{\alpha ,t}(r_0)$ lies in the exterior of ${\widehat{U}}_{\alpha ,t}$ as required. $\square$

Following the discussion in Section 2 of Erlandsson and Zakeri [3], we now apply Proposition 3.8 to all powers $A^q$ of A with $4|\sin (\pi q\alpha )|<1/2$. In particular, if if $p_{n+1}/q_{n+1}$ is a rational convergent of $\alpha$ with $q_{n+1}> 8\pi$ then we have $4|\sin (\pi q_n\alpha )|\le 4\pi /q_{n+1}<1/2$.

Proposition 3.9

Let N be a positive integer so that $q_N>8\pi$. Suppose that $\lambda _N\in (0,1]$ is a constant for which $q_n/q_{n+1}\le \lambda _N$ for all $n\ge N$. Let $\Delta _{{\mathbb {R}}}$ be defined by (17). Then for all $r\ge q_N^2t/2\pi$ we have

$$\begin{aligned} \widehat{{\mathcal {B}}}_{\alpha ,t}(r)< & {} \sqrt{\frac{(1+\lambda _N^2)2\pi tr}{\Delta _{{\mathbb {R}}}\bigl (2\sqrt{2\pi t/r}\bigr )}} \\= & {} \sqrt{1+\lambda _N^2}\Bigl (\sqrt{2\pi t r}+2\pi t+O(r^{-1/2})\Bigr ). \end{aligned}$$

Proof

For each $r\ge q_N^2t/2\pi$ there is an $n\ge N$ so that

$$\begin{aligned} \frac{q_n^2t}{2\pi }\le r\le \frac{q_{n+1}^2t}{2\pi }. \end{aligned}$$

Using Lemma 3.2, for r in this interval we have

$$\begin{aligned} 4\sin ^2(\pi q_n\alpha )^2r^2+q_n^2t^2\le (1+q_n^2/q_{n+1}^2)2\pi tr \le (1+\lambda _N^2)2\pi tr. \end{aligned}$$

Since $q_{n+1}\ge \sqrt{2\pi r/t}$, we also have

$$\begin{aligned} 4|\sin (\pi q_n\alpha )|< 4\pi /q_{n+1}\le 2\sqrt{2\pi t/r}. \end{aligned}$$

Also, since $r\ge q_N^2t/2\pi > 32\pi t$ we have $2\sqrt{2\pi t/r}<1/2$. This means that $2\sqrt{2\pi t/r}$ is in the domain of definition of $\Delta _{{\mathbb {R}}}$. Since $\Delta _{{\mathbb {R}}}$ is a decreasing function, this means:

$$\begin{aligned} \Delta _{{\mathbb {R}}}\bigl (4|\sin (\pi q_n\alpha )|\bigr ) >\Delta _{{\mathbb {R}}}\bigl (2\sqrt{2\pi t/r}\bigr ). \end{aligned}$$

Therefore, again for r in this interval, we have

$$\begin{aligned} \widehat{{\mathcal {B}}}_{\alpha ,t}(r)= & {} \inf _q\sqrt{\frac{4\sin ^2(\pi q\alpha )r^2+q^2t^2}{\Delta _{{\mathbb {R}}}\bigl (4|\sin (\pi q\alpha )|\bigr )}} \\\le & {} \sqrt{\frac{4\sin ^2(\pi q_n\alpha )r^2+q_n^2t^2}{\Delta _{{\mathbb {R}}}\bigl (4|\sin (\pi q_n\alpha )|\bigr )}} \\\le & {} \sqrt{\frac{(1+\lambda _N^2)2\pi tr}{\Delta _{{\mathbb {R}}}\bigl (2\sqrt{2\pi t/r}\bigr )}}. \end{aligned}$$

Finally, we give the asymptotic behaviour of this function as r tends to $\infty$. It is easy to see that $\Delta _{{\mathbb {R}}}(X)=1-X+O(X^2)$ and so $1/\sqrt{\Delta _{{\mathbb {R}}}(X)}=1+X/2+O(X^2)$. Thus

$$\begin{aligned} \sqrt{\frac{(1+\lambda _N^2)2\pi tr}{\Delta _{{\mathbb {R}}}\bigl (2\sqrt{2\pi t/r}\bigr )}} =\sqrt{1+\lambda _N^2}\Bigl (\sqrt{2\pi tr}+2\pi t+O(r^{-1/2})\Bigr ). \end{aligned}$$

$\square$

4 Complex hyperbolic space

4.1 Background on complex hyperbolic space

The Siegel domain model of complex hyperbolic space (see Goldman [4]) is given in polar horospherical coordinates by

$$\begin{aligned} \mathbf{H}^2_{{\mathbb {C}}}=\Bigl \{(r,\theta ,v,u)\in {{\mathbb {C}}}\times {{\mathbb {R}}}^2\ :\ u>0\Bigr \}. \end{aligned}$$

If $z_1$ and $z_2$ in $\mathbf{H}^2_{{\mathbb {C}}}$ have coordinates $z_1=(r_1,\theta _1,v_1,u_1)$ and $z_2=(r_2,\theta _2,v_2,u_2)$ then the complex hyperbolic (Bergman) distance $\rho (z_1,z_2)$ between them is given by

$$\begin{aligned} \cosh ^2\left( \frac{\rho (z_1,z_2)}{2}\right) =\frac{\bigl |r_1^2-2r_1r_2e^{i\theta _1-i\theta _2}+r_2^2+u_1+u_2-iv_1+iv_2\bigr |}{4u_1u_2}. \end{aligned}$$

We define complex hyperbolic horospheres, horoballs and sub-horospherical regions based at $\infty$ in a manner similar to their real hyperbolic counterparts (see Goldman [4]).

In what follows we want to consider discrete subgroups of complex hyperbolic isometries containing the screw parabolic map A given by:

$$\begin{aligned} A:(r,\theta ,v,u)\longmapsto (r,\theta +2\pi \alpha , v+t,u) \end{aligned}$$

(19)

where $t>0$ and $\alpha$ is irrational. For such a map its Bergman translation length $\rho \bigl (A(z),z\bigr )$ at $z=(r,\theta ,v,u)$ is given by

$$\begin{aligned} \cosh \left( \frac{\rho \bigl (A(z),z\bigr )}{2}\right) =\frac{\bigl |2(1-e^{2\pi i\alpha })r^2+2u-it\bigr |}{2u}. \end{aligned}$$

(20)

4.2 A sub-horospherical region contained in the Margulis region

The Bergman translation length of a screw parabolic map acting on complex hyperbolic space is rather more complicated than the analogous Poincaré translation length in the real case. Therefore, we use the following lemma to find a smaller precisely invariant sub-horospherical region.

Lemma 4.1

Suppose that $z=(r,\theta ,v,u)\in \mathbf{H}^2_{{\mathbb {C}}}$ satisfies

$$\begin{aligned} u>\frac{4|\sin (\pi q\alpha )|r^2+|qt|}{4\sinh ^2(\delta /4)} \end{aligned}$$

for some $\delta >0$. Then $\rho \bigl (A^q(z),z\bigr )<\delta$.

Proof

Using (20) we have

$$\begin{aligned} \cosh \left( \frac{\rho \bigl (A^q(z),z\bigr )}{2}\right)= & {} \frac{\bigl |2(1-e^{2\pi iq\alpha })r^2+2u-iqt\bigr |}{2u} \\\le & {} \frac{4|\sin (\pi q\alpha )|r^2+2u+|qt|}{2u} \\< & {} \frac{4\sinh ^2(\delta /4)u+2u}{2u} \\= & {} \cosh (\delta /2). \end{aligned}$$

$\square$

Let $\varepsilon$ be the Margulis constant for $\mathbf{H}^2_{{\mathbb {C}}}$ and, as before, let $c(\varepsilon /2)=1/2\sinh (\varepsilon /4)$. Then we define

$$\begin{aligned} U_{q\alpha ,qt}^{{\mathbb {C}}} =\Bigl \{(r,\theta ,v,u)\in \mathbf{}^2_{{\mathbb {C}}}\ :\ u>c(\varepsilon /2)^2\bigl (4|\sin (\pi q\alpha )|r^2+|qt|\bigr )\Bigr \}. \end{aligned}$$

Using Lemma 4.1 we see that for all $z\in U_{q\alpha ,qt}^{{\mathbb {C}}}$ the screw parabolic map $A^q$ has Bergman translation length strictly smaller than $\varepsilon$. Hence $U_{q\alpha ,qt}^{{\mathbb {C}}}$ is contained in the Margulis region and the Margulis region also contains:

$$\begin{aligned} T^{{\mathbb {C}}}_{\alpha ,t}=\bigcup _{q\ge 1}U_{q\alpha ,qt}^{{\mathbb {C}}} =\Bigl \{(r,\theta ,v,u)\in \mathbf{H}^2_{{\mathbb {C}}}\ :\ u>{{\mathcal {B}}}^{{\mathbb {C}}}_{\alpha ,t}(r)\Bigr \} \end{aligned}$$

with boundary function

$$\begin{aligned} {{\mathcal {B}}}^{{\mathbb {C}}}_{\alpha ,t}(r)=c(\varepsilon /2)^2 \inf _{q\ge 1} \bigl (4|\sin (\pi q\alpha )|r^2+qt\bigr ). \end{aligned}$$

This is the boundary function we want to estimate. A similar argument to Lemma 3.1 shows that for each r the infimum is attained for some q which is the denominator $q_n$ of a rational convergent of $\alpha$. (However, we do not know such a result if we simply use the boundary function given by constant Bergman translation length.) The following simple lemma is analogous to Lemma 3.2.

Lemma 4.2

Let $t>0$. Let $\alpha$ be irrational and let $p_n/q_n$, with $n\in {{\mathbb {N}}}$, be its rational convergents. Then for all r with

$$\begin{aligned} q_n\sqrt{\frac{t}{4\pi }}\le r\le q_{n+1}\sqrt{\frac{t}{4\pi }} \end{aligned}$$

we have

$$\begin{aligned} 4|\sin (\pi q_n\alpha )|r^2+q_nt < \left( 1+\frac{q_n}{q_{n+1}}\right) 2\sqrt{\pi t}\,r. \end{aligned}$$

Proof

Using Lemma 2.6, we have:

$$\begin{aligned} 4|\sin (\pi q_n\alpha )|r^2+q_nt< & {} \frac{4\pi r^2}{q_{n+1}}+q_nt \\= & {} \left( 1+\frac{q_n}{q_{n+1}}\right) 2\sqrt{\pi t}\,r +\left( \frac{2r\sqrt{\pi }}{q_{n+1}}-\sqrt{t}\right) \bigl (2r\sqrt{\pi }-q_n\sqrt{t}\bigr ) \\\le & {} \left( 1+\frac{q_n}{q_{n+1}}\right) 2\sqrt{\pi t}\,r. \end{aligned}$$

The final inequality follows from the range of r we have chosen. $\square$

Therefore, we can prove our main theorem in the complex case, which is analogous to Proposition 3.3.

Proposition 4.3

Given $N\in {{\mathbb {N}}}$, let $\lambda _N\in (0,1]$ be a constant for which $q_n/q_{n+1}\le \lambda _N$ for all $n\ge N$. Then, for all $r\ge q_N\sqrt{t/4\pi }$ we have

$$\begin{aligned} {{\mathcal {B}}}_{\alpha ,t}^{{\mathbb {C}}}(r)<c(\epsilon /2)^2(1+\lambda _N)2\sqrt{\pi t}\,r. \end{aligned}$$

In particular, taking $N=1$ and $\lambda _1=1$, for all for all $r\ge q_1\sqrt{t/4\pi }$ we have

$$\begin{aligned} {{\mathcal {B}}}_{\alpha ,t}^{{\mathbb {C}}}(r)<c(\epsilon /2)^24\sqrt{\pi t}\,r. \end{aligned}$$

Proof

Once again, for each $r\ge q_N\sqrt{t/4\pi }$ there is an $n\ge N$ so that $q_n\sqrt{t/4\pi }\le r\le q_{n+1}\sqrt{t/4\pi }$. On this interval we have

$$\begin{aligned} {{\mathcal {B}}}^{{\mathbb {C}}}_{\alpha ,t}(r)= & {} c(\varepsilon /2)^2\, \inf _{q\ge 1} \bigl (4\sin (\pi q\alpha )r^2+qt^2\bigr ) \\\le & {} c(\varepsilon /2)^2\bigl ( 4\sin (\pi q_n\alpha )r^2+q_nt\bigr ) \\\le & {} c(\varepsilon /2)^2(1+q_n/q_{n+1})2\sqrt{\pi t}\,r \\\le & {} c(\varepsilon /2)^2(1+\lambda _N)2\sqrt{\pi t}\,r. \end{aligned}$$

This gives the first estimate. The second follows by using $\lambda _N\le 1$. $\square$

We could also use an argument similar to Proposition 3.5 to give a lower bound on ${{\mathcal {B}}}^{{\mathbb {C}}}_{\alpha ,t}(r)$ that grows like $r^{2/\nu }$ when $\alpha$ is Diophantine of exponent $\nu$. However, unlike in the real hyperbolic case, ${{\mathcal {B}}}^{{\mathbb {C}}}_{\alpha ,t}(r)$ does not represent the boundary of the Margulis region, but only an upper bound. In the next section we show that when estimating a lower bound, one cannot do better than a constant function of r.

4.3 Points in the Margulis region on the same horosphere

In this section we construct a horosphere containing an unbounded sequence of points in the Margulis region. Therefore, any lower bound on the Margulis region in terms of r can be at best constant. This construction is based on the following phenomenon. When $\sin (\pi \alpha )$ and t have opposite signs, the Bergman translation length of $A=A_{\alpha ,t}$ is not a monotone function of r. (Such a screw-parabolic map is sometimes called negatively oriented, see Kamiya and Parker [8].) Since $\alpha -p_n/q_n<0$ when $n=2m-1$ is odd, we see that $\sin (\pi q_{2m-1}\alpha )$ is negative; that is, it has the opposite sign to $q_{2m-1}t$, which we always assume is positive.

Qualitatively, the Bergman translation length of $A^{q_{2m-1}}$ on a given horosphere whose height is small compared with $q_{2m-1}$ has the following behaviour. As r ranges from 0 to $\infty$, the translation length initially decreases to a minimum at some $r=r^{\min }_m$ and then grows. As m increases, so the value of $r^{\min }_m$ tends to infinity. But crucially, as this happens, the minimum translation length of $A^{q_{2m-1}}$ remains uniformly bounded. Our goal will be to show that there is a horosphere $H_{u_0}$ so that this translation length is at most the Margulis constant. To do so, we will find a sequence of points $z_m$ in $H_{u_0}$ that leaves every compact set with the property that for each $z_m$ the translation length of $A^{q_{2m-1}}$ at $z_m$ is at most the Margulis constant. To make the calculations slightly simpler we choose $z_m=(r_m,\theta _m,v_m,u_0)$ so that $r_m$ is not $r^{\min }_m$ but some nearby value where the translation length is still uniformly bounded. This will not affect the conclusion.

We begin with a simple lemma.

Lemma 4.4

Let $\alpha$ be irrational and let $p_n/q_n$ be its rational convergents. Then for $n\ge 3$ we have

$$\begin{aligned} |\tan (\pi q_n\alpha )|\le 4/q_{n+1}. \end{aligned}$$

Proof

This is proved in a similar way to Lemma 2.6. We use

$$\begin{aligned} |\pi q_n\alpha -\pi p_n|\le \pi /q_{n+1}. \end{aligned}$$

For $n\ge 3$ we have $q_{n+1}\ge 4$ and so the right hand side is at most $\pi /4$. Finally, for $0<x\le \pi /4$ we have $0<\tan (x)\le 4x/\pi$. $\square$

Now we can make the main construction of this section.

Proposition 4.5

Let $u_0=4c(\varepsilon /2)^2\lambda _N t$. For any positive constant $r_0$ there exists an integer $q\ge 1$ and a point $z=(r,\theta ,v,u_0)$ on the horosphere $H_{u_0}$ of height $u_0$ so that $r>r_0$ and $\rho \bigl (A^q(z),z\bigr )\le \varepsilon$.

Proof

Using (20) we have

$$\begin{aligned} \cosh \left( \frac{\rho \bigl (A^{q_n}(z),z\bigr )}{2}\right) = \frac{\bigl |2(1-e^{2\pi iq_n\alpha })r^2+2u-iq_nt\bigr |}{2u}. \end{aligned}$$

We have

$$\begin{aligned}&2(1-e^{2\pi iq_n\alpha })r^2+2u-iq_nt \\&\quad = 2r^2\bigl (1-\cos (2\pi q_n\alpha )\bigr )+2u -2ir^2\sin (2\pi q_n\alpha )r^2-iq_nt \\&\quad = 4r^2\sin ^2(\pi q_n\alpha )+2u -4ir^2\sin (\pi q_n\alpha )\cos (\pi q_n\alpha )-iq_nt. \end{aligned}$$

Choose r so that $\bigl (2(1-e^{2\pi iq_n\alpha })r^2+2u-iq_nt\bigr )$ is real. This necessarily means that $4\sin (\pi q_n\alpha )\cos (\pi q_n\alpha )<0$ and so $n=2m-1$ is odd. Specifically, it means that $r=r_{2m-1}$ where:

$$\begin{aligned} r_{2m-1}^2=\frac{q_{2m-1}t}{-4\sin (\pi q_{2m-1}\alpha )\cos (\pi q_{2m-1}\alpha )} =\frac{q_{2m-1}t}{4|\sin (\pi q_{2m-1}\alpha )\cos (\pi q_{2m-1}\alpha )|}. \end{aligned}$$

(21)

Note that

$$\begin{aligned} r_{2m-1}^2=\frac{q_{2m-1}t}{2|\sin (2\pi q_{2m-1}\alpha )|}>\frac{q_{2m-1}q_{2m}t}{4\pi }. \end{aligned}$$

Hence, by choosing m large enough, we can make $r_{2m-1}>r_0$ for any $r_0>0$. Moreover,

$$\begin{aligned} 2(1-e^{2\pi iq_{2m-1}\alpha })r_{2m-1}^2+2u-iq_{2m-1}t= & {} 4r_{2m-1}^2\sin ^2(\pi q_{2m-1}\alpha )+2u \\= & {} \frac{4q_{2m-1}t\sin ^2(\pi q_{2m-1}\alpha )}{4|\sin (\pi q_{2m-1}\alpha )\cos (\pi q_{2m-1}\alpha )|}+2u \\= & {} q_{2m-1}t|\tan (\pi q_{2m-1}\alpha )|+2u. \end{aligned}$$

Let $z_{2m-1}=(r_{2m-1},\theta ,v,u_0)$ where $r_{2m-1}$ is given by (21) and

$$\begin{aligned} u_0=4c(\varepsilon /2)^2\lambda _N t=\frac{\lambda _N t}{\sinh ^2(\varepsilon /4)}. \end{aligned}$$

Assume $n=2m-1\ge 3$, then using Lemma 4.4, we have

$$\begin{aligned} 2\sinh ^2\left( \frac{\rho \bigl (A^{q_{2m-1}}(z_{2m-1}),z_{2m-1}\bigr )}{4}\right)= & {} \cosh \left( \frac{\rho \bigl (A^{q_{2m-1}}(z_{2m-1}),z_{2m-1}\bigr )}{2}\right) -1 \\= & {} \frac{\bigl |2(1-e^{2\pi iq_{2m-1}\alpha })r_{2m-1}^2+2u_0-iq_{2m-1}t\bigr |-2u_0}{2u_0} \\= & {} \frac{q_{2m-1}t|\tan (\pi q_{2m-1}\alpha )|}{8c(\varepsilon /2)^2\lambda _Nt} \\\le & {} \frac{4q_{2m-1}/q_{2m}}{8c(\varepsilon /2)^2\lambda _N} \\\le & {} \frac{1}{2c(\varepsilon /2)^2} \\= & {} 2\sinh ^2(\varepsilon /4). \end{aligned}$$

Here $\lambda _N\in (0,1]$ is a constant so that $q_{2m-1}/q_{2m}\le \lambda _N$ for all $2m-1\ge N$. Thus $\rho \bigl (A^{q_{2m-1}}(z_{2m-1}),z_{2m-1}\bigr )\le \varepsilon$ as claimed. $\square$

We remark that this result does not imply that there is an invariant horosphere. We now show that we can find a sequence of points on horospheres whose height tends to infinity so that $A^{q_n}$ has a Bergman translation length greater than the Margulis constant for all $q_n$.

Proposition 4.6

Let m be a positive integer. Define $r_{2m}$ and $u_{2m}$ by

$$\begin{aligned} r_{2m}^2=\frac{(q_{2m+1}+q_{2m-1})t}{2\bigl (|\sin (2\pi q_{2m+1}\alpha )|+|\sin (2\pi q_{2m-1}\alpha )|\bigr )},\qquad u_{2m}=\frac{q_{2m}t}{4\cosh (\varepsilon /2)}. \end{aligned}$$

Then for all $n\in {{\mathbb {N}}}$ the Bergman translation length of $A^{q_n}$ at $z_{2m}=(r_{2m},\theta ,v,u_{2m})$ satisfies $\rho \bigl (A^{q_n}(z_{2m}),z_{2m}\bigr )>\varepsilon$.

Proof

Using (20), we see that the Bergman translation length of $A^q$ at the point $z=(r,\theta ,v,u)$ satisfies

$$\begin{aligned} \cosh \left( \frac{\rho \bigl (A^q(z),z\bigr )}{2}\right)= & {} \frac{\bigl |2r^2(1-\cos (2\pi q\alpha ))+2u-2ir^2\sin (2\pi q\alpha )-iqt\bigr |}{2u} \\> & {} \frac{\bigl |2r^2\sin (2\pi q\alpha )+qt\bigr |}{2u}. \end{aligned}$$

We now estimate the right hand side for various values of q. We will use

$$\begin{aligned} |\sin (2\pi q_{2m-1}\alpha )|>\frac{1}{2}\bigl ( |\sin (2\pi q_{2m-1}\alpha )|+|\sin (2\pi q_{2m+1}\alpha )|\bigr ) >|\sin (2\pi q_{2m+1}\alpha )|. \end{aligned}$$

• (1) For $1\le q\le q_{2m-1}$, using Lemma 2.2, we have $\bigl |\sin (2\pi q\alpha )\bigr |\ge \bigl |\sin (2\pi q_{2m-1}\alpha )\bigr |$. This includes all $q_n$ with $n\le 2m-1$. This means that

  $$\begin{aligned}&\bigl |2r_{2m}^2\sin (2\pi q\alpha )+qt\bigr | \\&\quad \ge 2r_{2m}^2\bigl |\sin (2\pi q\alpha )\bigr |-qt \\&\quad \ge 2r_{2m}^2\bigl |\sin (2\pi q_{2m-1}\alpha )\bigr |-q_{2m-1}t \\&\quad = \frac{(q_{2m+1}+q_{2m-1})t}{|\sin (2\pi q_{2m+1}\alpha )|+|\sin (2\pi q_{2m-1}\alpha )|}\, \bigl |\sin (2\pi q_{2m-1}\alpha )\bigr |-q_{2m-1}t \\&\quad = \frac{q_{2m+1}t|\sin (2\pi q_{2m-1}\alpha )|-q_{2m-1}t|\sin (2\pi q_{2m+1}\alpha )|}{|\sin (2\pi q_{2m+1}\alpha )|+|\sin (2\pi q_{2m-1}\alpha )|} \\&\quad > (q_{2m+1}-q_{2m-1})t/2 \\&\quad \ge q_{2m}t/2. \end{aligned}$$

  In the last line we used $q_{2m+1}=a_{2m}q_{2m}+q_{2m-1}\ge q_{2m}+q_{2m-1}$.

• (2) Suppose that $q\ge q_{2m+1}$ with $\bigl |\sin (2\pi q\alpha )\bigr |\le \bigl |\sin (2\pi q_{2m+1}\alpha )\bigr |$. This includes all $q_n$ with $n\ge 2m+1$. In this case, we have

  $$\begin{aligned}&\bigl |2r_{2m}^2\sin (2\pi q\alpha )+qt\bigr | \\&\quad \ge qt-2r_{2m}^2\bigl |\sin (2\pi q\alpha )\bigr | \\&\quad \ge q_{2m+1}t-2r_{2m}^2\bigl |\sin (2\pi q_{2m+1}\alpha )\bigr | \\&\quad = q_{2m+1}t-\frac{(q_{2m+1}+q_{2m-1})t}{|\sin (2\pi q_{2m+1}\alpha )|+|\sin (2\pi q_{2m-1}\alpha )|}\, \bigl |\sin (2\pi q_{2m+1}\alpha )\bigr | \\&\quad = \frac{q_{2m+1}t|\sin (2\pi q_{2m-1}\alpha )|-q_{2m-1}t|\sin (2\pi q_{2m+1}\alpha )|}{|\sin (2\pi q_{2m+1}\alpha )|+|\sin (2\pi q_{2m-1}\alpha )|} \\&\quad > q_{2m}t/2. \end{aligned}$$

• (3) Suppose that $q\ge q_{2m}$ and $\sin (2\pi q\alpha )>0$, which includes $q_{2m}$. In this case

  $$\begin{aligned} \bigl |2r_{2m}^2\sin (2\pi q\alpha )+qt\bigr | =2r_{2m}^2\sin (2\pi q\alpha )+qt > qt\ge q_{2m}t. \end{aligned}$$

In each case we have

$$\begin{aligned} \cosh \left( \frac{\rho \bigl (A^{q_n}(z_{2m}),z_{2m}\bigr )}{2}\right)> \frac{\bigl |2r_{2m}^2\sin (2\pi q_n\alpha )+q_nt\bigr |}{2u_{2m}} > \frac{q_{2m}t}{4u_{2m}}=\cosh (\varepsilon /2). \end{aligned}$$

This completes the proof. $\square$

Note that this proof works for all q except for those which satisfy both $q > q_{2m-1}$ and $\sin (2\pi q\alpha )<-\bigl |\sin (2\pi q_{2m+1}\alpha )\bigr |<0$. The main problem is that for these points we cannot rule out the possibility that $r_{2m}^2$ is close to $qt/\bigl |2\sin (2\pi q\alpha )\bigr |$, which would mean we could apply an argument similar to Proposition 4.5 to find points $(r_{2m},0,0,u_0)$ in the Margulis region for some universal $u_0$. On the other hand, if we could show Proposition 4.6 for such values of q, then we would have constructed points not in the Margulis region that lie on horospheres of arbitrary height.

4.4 An explicit bound using the region of Cao and Parker

This section follows the ideas in Sect. 3.6 where Waterman’s bound on the radii of isometric spheres is replaced by the following analogous statement for $\mathbf{H}^2_{{\mathbb {C}}}$. In Theorem 1.3 of [1], Cao and Parker define

$$\begin{aligned} K=\frac{1+2|e^{2\pi i\alpha }-1| +\sqrt{1-12|e^{2\pi i\alpha }-1|+4|e^{2\pi i\alpha }-1|^2}}{2}. \end{aligned}$$

and then show that the sub-horospherical region defined by

$$\begin{aligned} u>\frac{|2(e^{2\pi i\alpha }-1)r^2+it|}{K} +\frac{8|e^{2\pi i\alpha }-1|^2r^2}{K(K-4|e^{2\pi i\alpha }-1|)} \end{aligned}$$

is precisely invariant. This follows from their bound on the radii of isometric spheres analogous to Theorem 3.7.

We choose to weaken the bound of this sub-horospherical region. We have

$$\begin{aligned}&\frac{|2(e^{2\pi i\alpha }-1)r^2+it|}{K} +\frac{8|e^{2\pi i\alpha }-1|^2r^2}{K(K-4|e^{2\pi i\alpha }-1|)} \\&\quad \le \frac{4|\sin (\pi \alpha )|r^2+t}{K} +\frac{32\sin ^2(\pi \alpha )r^2}{K(K-8|\sin (\pi \alpha )|)} \\&\quad = \frac{4|\sin (\pi \alpha )|r^2}{K-8|\sin (\pi \alpha )|} +\frac{t}{K} \\&\quad \le \frac{4|\sin (\pi \alpha )|r^2+t}{K-8|\sin (\pi \alpha )|}. \end{aligned}$$

Therefore, we choose to use the region where

$$\begin{aligned} u>\frac{4|\sin (\pi \alpha )|r^2+t}{K-8|\sin (\pi \alpha )|}. \end{aligned}$$

Note that

$$\begin{aligned} K-8|\sin (\pi \alpha )| =\frac{1-12|\sin (\pi \alpha )|+\sqrt{1-24|\sin (\pi \alpha )|+16\sin ^2(\pi \alpha )}}{2}. \end{aligned}$$

For $0<X<\bigl (\sqrt{2}-1\bigr )^2$ define

$$\begin{aligned} \Delta _{{\mathbb {C}}}(X)=\frac{1-3X+\sqrt{1-6X+X^2}}{2} =\frac{\bigl (1+\sqrt{1-6X+X^2}\bigr )^2-X^2}{4} \end{aligned}$$

(22)

so that $K-8|\sin (\pi \alpha )|=\Delta _{{\mathbb {C}}}\bigl (4|\sin (\pi \alpha )|\bigr )$. We note that $\Delta _{{\mathbb {C}}}$ is a decreasing function of X in the interval $0<X<\bigl (\sqrt{2}-1\bigr )^2$. Therefore the following theorem is a corollary of Theorem 1.3 of [1]:

Proposition 4.7

Let $\Gamma$ be a discrete subgroup of $\mathrm{Isom}(\mathbf{H}^2_{{\mathbb {C}}})$ containing A of the form (19). Suppose that $t>0$ and $4|\sin (\pi \alpha )|<\bigl (\sqrt{2}-1\bigr )^2$ where $\alpha$ is irrational. If $\Delta _{{\mathbb {C}}}(x)$ is given by (22) then define

$$\begin{aligned} {\widehat{U}}_{\alpha ,t}^{{\mathbb {C}}}=\left\{ (r,\theta ,v,u)\in \mathbf{H}^2_{{\mathbb {C}}}\ :\ u>\frac{4\sin ^2(\pi \alpha )r^2+t}{\Delta _{{\mathbb {C}}}\bigl (4|\sin (\pi \alpha )|\bigr )}. \right\} . \end{aligned}$$

Then ${\widehat{U}}^{{\mathbb {C}}}_{\alpha ,t}$ is precisely invariant under $\Gamma _\infty$ in $\Gamma$.

Therefore, we define

$$\begin{aligned} \widehat{{\mathcal {B}}}_{\alpha ,t}^{{\mathbb {C}}}(r) =\inf _q\, \frac{4\sin ^2(\pi q\alpha )r^2+qt}{\Delta _{{\mathbb {C}}}\bigl (4|\sin (\pi q\alpha )|\bigr )} \end{aligned}$$

where the infimum is taken over all positive integers q with $4|\sin (\pi q\alpha )|<\bigl (\sqrt{2}-1\bigr )^2$.

Proposition 4.8

Let $\Gamma$ be a discrete subgroup of $\mathrm{Isom}(\mathbf{H}^2_{{\mathbb {C}}})$ containing A of the form (19), where $t>0$ and $\alpha$ is irrational. Let $\Delta _{{\mathbb {C}}}(X)$ be given by (22). Let N be a positive integer so that $q_N>4\pi /\bigl (\sqrt{2}-1\bigr )^2$. Let $\lambda _N\in (0,1]$ be a constant so that $q_n/q_{n+1}\le \lambda _N$ for all $n\ge N$. Then for all $r\ge q_N\sqrt{t/4\pi }$ we have:

$$\begin{aligned} \widehat{{\mathcal {B}}}_{\alpha ,t}^{{\mathbb {C}}}(r)< & {} \frac{(1+\lambda _N)2\sqrt{\pi t}\,r}{\Delta _{{\mathbb {C}}}(2\sqrt{\pi t}/r)} \\= & {} (1+\lambda _N)\bigl (2\sqrt{\pi t}\,r+12\pi t\bigr )+O(r^{-1}). \end{aligned}$$

Proof

Consider the interval

$$\begin{aligned} q_n\sqrt{\frac{t}{4\pi }}\le r\le q_{n+1}\sqrt{\frac{t}{4\pi }} \end{aligned}$$

where $n\ge N$. Using Lemma 4.2 we have

$$\begin{aligned} 4|\sin (\pi q_n\alpha )|r^2+q_nt \le \left( 1+\frac{q_n}{q_{n+1}}\right) 2\sqrt{\pi t}\,r \le \left( 1+\lambda _N\right) 2\sqrt{\pi t}\,r. \end{aligned}$$

We also have

$$\begin{aligned} 4|\sin (\pi q_n\alpha )|<4\pi /q_{n+1}<2\sqrt{\pi t}/r. \end{aligned}$$

Since $q_N>4\pi /\bigl (\sqrt{2}-1\bigr )^2$ we have

$$\begin{aligned} \frac{2\sqrt{\pi t}}{r} \le \frac{2\sqrt{\pi t}}{q_n\sqrt{t/4\pi }} =\frac{4\pi }{q_n}\le \frac{4\pi }{q_N}<\bigl (\sqrt{2}-1\bigr )^2. \end{aligned}$$

Therefore $2\sqrt{\pi t}/r$ is in the domain of definition of $\Delta _{{\mathbb {C}}}$ and since $\Delta _{{\mathbb {C}}}$ is a decreasing function,

$$\begin{aligned} \Delta _{{\mathbb {C}}}\bigl (4|\sin (\pi q_n\alpha )|\bigr )> \Delta _{{\mathbb {C}}}\bigl (2\sqrt{\pi t}/r\bigr ). \end{aligned}$$

Then:

$$\begin{aligned} \widehat{{\mathcal {B}}}_{\alpha ,t}^{{\mathbb {C}}}(r)= & {} \inf _q \frac{4\sin ^2(\pi q\alpha )r^2+qt}{\Delta _{{\mathbb {C}}}(4|\sin (\pi q\alpha )|)} \\\le & {} \frac{4\sin ^2(\pi q_n\alpha )r^2+q_nt}{\Delta _{{\mathbb {C}}}(4|\sin (\pi q_n\alpha )|)} \\\le & {} \frac{(1+\lambda _N)2\sqrt{\pi t}\,r}{\Delta _{{\mathbb {C}}}(2\sqrt{\pi t}/r)}. \end{aligned}$$

This gives the first statement. For the second, we want to estimate the asymptotic behaviour of this function. It is easy to see that $\Delta _{{\mathbb {C}}}(X)=1-3X+O(X^2)$ and so $1/\Delta _{{\mathbb {C}}}(X)=1+3X+O(X^2)$. Hence

$$\begin{aligned} \frac{2\sqrt{\pi t}(1+\lambda _N)r}{\Delta _{{\mathbb {C}}}(2\sqrt{\pi t}/r)} =(1+\lambda _N)\bigl (2\sqrt{\pi t}\,r+12\pi t\bigr )+O(r^{-1}). \end{aligned}$$

$\square$