Abstract
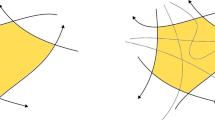
We study self-affine tiles which tile the n-dimensional real vector space with respect to a crystallographic group. First we define classes of graphs that allow to determine the neighbors of a given tile algorithmically. In the case of plane tiles these graphs are used to derive a criterion for such tiles to be homeomorphic to a disk. As particular application, we will solve a problem of Gelbrich, who conjectured that certain examples of tiles which tile \({\mathbb{R}}^2\) with respect to the ornament group p2 are homeomorphic to a disk.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Akiyama S. and Thuswaldner J.M. (2004). A survey on topological properties of tiles related to number systems. Geom. Dedicata 109: 89–105
Akiyama S. and Thuswaldner J.M. (2005). The topological structure of fractal tilings generated by quadratic number systems. Comput. Math. Appl. 49: 1439–1485
Bandt C. and Wang Y. (2001).Disk-like self-affine tiles in \({\mathbb{R}}^2\). Discrete Comput. Geom. 26: 591–601
Burckhardt J. (1974). Die Bewegungsgruppen der Kristallographie. Birkhäuser, Basel
Gelbrich G. (1994). Crystallographic reptiles. Geom. Dedicata 51: 235–256
Grünbaum B. and Shephard G. (1987). Tilings and patterns. Freeman, New York
Hata M. (1985). On the structure of self-similar sets. Jpn. J. Appl. Math. 2: 381–414
Hutchinson J.E. (1981). Fractals and self-similarity. Indiana Univ. Math. J 30: 713–747
Kuratowski, K.: Topology. Vol. II, New edition, revised and augmented. Translated from the French by A. Kirkor, Academic Press, New York (1968)
Luo J., Akiyama S. and Thuswaldner J.M. (2004). On the boundary connectedness of connected tiles. Math. Proc. Camb. Phil. Soc. 137: 397–410
Luo J., Rao H. and Tan B. (2002). Topological structure of self-similar sets. Fractals 10: 223–227
Luo J. and Zhou Z.L. (2004). Disk-like tiles derived from complex bases. Acta Math. Sin. (Engl. Ser.) 20: 731–738
Ngai S.-M. and Nguyen N. (2003). The Heighway dragon revisited. Discrete Comput. Geom. 29: 603–623
Ngai S.-M. and Tang T.-M. (2004). A technique in the topology of connected self-similar tiles. Fractals 12: 389–403
Ngai S.-M. and Tang T.-M. (2005). Topology of connected self-similar tiles in the plane with disconnected interiors. Topology Appl. 150: 139–155
Scheicher, K., Thuswaldner, J.-M.: Fractals in Graz 2001, Birkhäuser Verlag (2002)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Loridant, B., Luo, J. & Thuswaldner, J.M. Topology of crystallographic tiles. Geom Dedicata 128, 113–144 (2007). https://doi.org/10.1007/s10711-007-9186-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10711-007-9186-0