Skip to main content
SpringerLink
Log in

Querying visible points in large obstructed space

  • Published:
GeoInformatica Aims and scope Submit manuscript

Abstract

Querying visible points is a fundamental problem in computational geometry and spatial databases. With the development of new applications such as trip planning and nearest neighbors, querying visible points plays a key role in obstacle space and the result can be further used such as defining the shortest path. Thereby, efficiently finding the result is essentially important. However, the performance of current methods decrease substantially for large datasets. To solve the problem, we proposes a new and fast algorithm to find visible points for an arbitrary query location inside a large polygon containing obstacles. The method is based on polygon triangulation. By decomposing the polygon into a set of triangles, we manage the polygon by organizing triangles in an efficient way instead of maintaining a large number of vertices. We propose a data structure to partition the searching space into several parts, each of which is independently processed. Afterwards, by recursively calling a method we search visible points by accessing triangles and return the result in a progressive way. Through a theoretical analysis, assuming the polygon contains N vertices in total, the time complexity of our algorithm is O(N), improving the existing method O(N l o g N). We prove the correctness of the algorithm and analyze the space complexity, which is O(N). The technique is extended to return visible points less than a threshold distance to the query location. Using both synthetic and real datasets, we perform extensive experiments to test our algorithm and demonstrate its efficiency and effectiveness. Visible points are efficiently processed in a large obstacle space with over one million vertices. Experimental results show that our technique gains more than one order of magnitude speedup compared to competitive methods using large datasets.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20

Similar content being viewed by others

Notes

  1. Using the algebraic terminology that for a data type α, its domain or carrier set is denoted as D α .

  2. 2Every internal angle is less than 180 degrees.

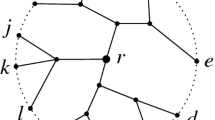
  3. If we choose the method of checking the relationship between the invisible area and an vertex, merging two areas involves a costly operation, performing the union on two regions.

References

  1. http://dna.fernuni-hagen.de/secondo.html/index.html.

  2. http://www.bbbike.de/cgi-bin/bbbike.cgi(2012.6.25)

  3. http://www.census.gov/geo/www/tiger/tgrshp2010/tgrshp2010.html(2012.6.25).

  4. http://www.chorochronos.org/?q=node/59(2013.8)

  5. Ben-Moshe B, Hall-Holt OA, Katz MJ, Mitchell JSB (2004) Computing the visibility graph of points within a polygon. In: symposium on computational geometry, pp 27–35

  6. Chazelle B (1982) A theorem on polygon cutting with applications.In: IEEE symposium on foundations of computer science

  7. De Berg M, Kreveld M, Overmars M, Schwarzkopf O (2000) Computational geometry:algorithms and applications, 2nd edn. Springer, Berlin

    Book  Google Scholar 

  8. Gao Y, Zheng B (2009) Continuous obstructed nearest neighbor queries in spatial databases.In: SIGMOD, pp 577–590

  9. Gao Y, Zheng B, Chen G, Lee WC, Lee KCK, Li Q (2009) Visible reverse k-nearest neighbor query processing in spatial databases. TKDE 21(9):1314–1327

    Google Scholar 

  10. Gao Y, Zheng B, Lee W, Chen G (2009) Continuous visible nearest neighbor queries. In: EDBT, pp 144–155

  11. Ghosh S K (2007) Visibility algorithms in the plane. Cambridge University Press, United Kingdom

    Book  Google Scholar 

  12. Ghosh SK, Mount DM (1991) An output-sensitive algorithm for computing visibility graphs. SIAM J Comput 20(5):888–910

    Article  Google Scholar 

  13. Guibas L, Hershberger J, Leven D, Sharir M, Tarjan RE (1987) Linear-time algorithms for visibility and shortest path problems inside triangulated simple polygons. Algorithmica 2:209–233

    Article  Google Scholar 

  14. Held M (2001) Fist:fast industrial-strength triangulation of polygons. Algorithmica 30(4):563–596

    Article  Google Scholar 

  15. Hershberger J, Snoeyink J (1994) Computing minimum length paths of a given homotopy class. Comp Geom Theory and Appl 4:63–97

    Article  Google Scholar 

  16. Hershberger J, Suri S (1999) An optimal algorithm for euclidean shortest paths in the plane. SIAM J Comput 28(6):2215–2256

    Article  Google Scholar 

  17. Kapoor S, Maheshwari SN, Mitchell JSB (1997) An efficient algorithm for euclidean shortest paths among polygonal obstacles in the plane. Discrete Comput Geom 18:377–383

    Article  Google Scholar 

  18. Kazemi L, Kashani FB, Shahabi C, Jain R (2010) Efficient approximate visibility query in large dynamic environments. In: DASFAA (1), pp 202–217

  19. Lee DT, Preparata FP (1984) Euclidean shortest paths in the presence of rectilinear barriers. Networks 14(3):393–410

    Article  Google Scholar 

  20. Masud S, Choudhury F M, Ali M E, Nutanong S (2013) Maximum visibility queries in spatial databases. In: ICDE, pp 637–648

  21. Mitchell JSB (1996) Shortest paths among obstacles in the plane. Internet Journal Comput Geom 6:309–332

    Article  Google Scholar 

  22. Narkhede A, Manocha D (1995) Fast polygon triangulation based on Seidel’s algorithm. Academic Press, Graphics Gems V

    Book  Google Scholar 

  23. Nutanong S, Tanin E, Zhang R (2007) Visible nearest neighbor queries. In: DASFAA, pp 876–883

  24. Overmars M H, Welz E (1988) New methods for computing visibility graphs.In: Proceedings 4th annual ACM symposium on computational geometry, pp 164–171

  25. Park SH, Lee JH, Kim DH (2007) Spatial clustering based on moving distance in the presence of obstacles. In: DASFAA, pp 1024–1027

  26. Pocchiola M, Vegter G (1995) Minimal tangent visibility graph. Comput Geom Theor Appl 6:303–314

    Article  Google Scholar 

  27. Sharir M, Schorr A (1986) On shortest paths in polyhedral spaces. SIAM J Comput 15(1):193–215

    Article  Google Scholar 

  28. Storer JA, Reif JH (1994) Shortest paths in the plane with polygonal obstacles. J ACM 41(5):982–1012

    Article  Google Scholar 

  29. Asano T, Ghosh SK, Shermer TC (2000) Visibility in the plane.Handbook of computation geometry. Elsevier

  30. Tung AKH, Hou J, Han J (2001) Spatial clustering in the presence of obstacles. In: ICDE, pp 359–367

  31. Xia C, Hsu D, Tung AKH (2004) A fast filter for obstructed nearest neighbor queries. In: BNCOD, pp 203–215

  32. Xu J, Güting RH (2012) MWGen:a mini world generator. In: MDM, pp 258–267

  33. Yang B, Lu H, Jensen CS (2009) Scalable continuous range monitoring of moving objects in symbolic indoor space. In: CIKM, pp 671–680

  34. Yang B, Lu H, Jensen CS (2010) Probabilistic threshold k nearest neighbor queries over moving objects in symbolic indoor space. In: EDBT, pp 335–346

  35. Zaïane OR, Lee CH (2002) Clustering spatial data in the presence of obstacles: a density-based approach. In: IDEAS, pp 214–223

  36. Zhang J, Papadias D, Mouratidis K, Zhu M (2004) Spatial queries in the presence of obstacles. In: EDBT

  37. Zhang J, Papadias D, Mouratidis K, Zhu M (2005) Query processing in spatial databases containing obstacles. Int J Geogr Inf Sci 19(10):1091–1111

    Article  Google Scholar 

Download references

Acknowledgment

This work is supported in part by NSFC under grants 61300052, the Fundamental Research Funds for the Central Universities under grants NZ2013306 and Natural Science Foundation of Jiangsu Province of China under grants BK20130810. The first author thanks Bin Yao for helpful comments on the revised version of this paper.

Author information

Authors and Affiliations

  1. Nanjing University of Aeronautics and Astronautics, Nanjing Jiangsu, China

    Jianqiu Xu

  2. Fern Universität in Hagen, Hagen, Germany

    Ralf Hartmut Güting

Authors
  1. Jianqiu Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ralf Hartmut Güting
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jianqiu Xu.

Additional information

Part of the work is done when the author is a Ph.D student in FernUniversität in Hagen, Germany.

Appendix: Experimental statistics

Appendix: Experimental statistics

Fig. 21
figure 21

Statistics for evaluation of dataset size

Full size image
Fig. 22
figure 22

Berlin and Houston

Full size image
Fig. 23
figure 23

California-I

Full size image
Fig. 24
figure 24

California-II

Full size image
Fig. 25
figure 25

Time cost (sec.) for angle

Full size image
Fig. 26
figure 26

Time cost (sec.) for visible points within a range

Full size image

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xu, J., Güting, R.H. Querying visible points in large obstructed space. Geoinformatica 19, 435–461 (2015). https://doi.org/10.1007/s10707-014-0213-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10707-014-0213-7

Keywords

Search

Navigation