Abstract
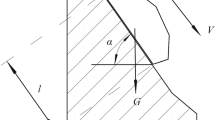
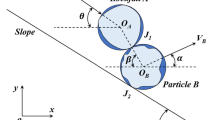
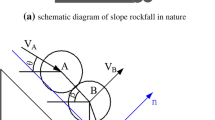
Rockfall is one of the common geological disasters in China, which causes huge losses to the country and the people. Based on the impulse and impulse moment theorems, and considering the stochastic factors in the process of rolling stone collision, a stochastic collision model of the rockfall-wall is established, and the analytical solution for the velocity of the rolling stone after collision is obtained. When considering the initial rotation of the rolling stone, the predicted result from the model agrees with the experimental result, and when the initial rotation is ignored, the result obtained from the model will underestimate/overestimate the rebound velocity, and the maximum reaches 20%. Furthermore, the probability distribution and the fit curve for the velocity and trajectory of the rolling stone depends on the project. The result shows that the rebound velocity and angle of the rolling stone follow a typical Gaussian distribution, and the horizontal distance and bounce height follow the Gaussian and exponential distribution, respectively. The prediction of the velocity and trajectory of the rolling stone provides a theoretical basis for the optimal design of engineering structures.





Similar content being viewed by others
References
Abdelhady MS, Rindt CC, Wijers JGJ et al (2006) Modelling the impaction of a micron particle with a powdery layer. Powder Technol 168(3):111–124
Asteriou P, Tsiambaos G (2016) Empirical model for predicting rockfall trajectory direction. Rock Mech Rock Eng 49(3):927–941
Azzoni A, Freitas MHD (1995) Experimentally gained parameters, decisive for rock fall analysis. Rock Mech Rock Eng 28(2):111–124
Bourrier F, Dorren L, Nicot F et al (2009) Toward objective rockfall trajectory simulation using a stochastic impact model. Rock Mech Rock Eng 110(3–4):79
Chau KT, Wong RHC, Wu JJ (2002) Coefficient of restitution and rotational motions of rockfall impacts. Int J Rock Mech Min Sci 39(1):69–77
Cui SH, Pei XJ, Huang RQ (2017) Rolling motion behavior of rockfall on gentle slope: an experimental approach. J Mt Sci 14(8):1550–1562
Delhomme F, Mommessin M, Mougin JP et al (2005) Behavior of a structurally dissipating rock-shed: experimental analysis and study of punching effects. Int J Solids Struct 42(14):4204–4219
Dong H, Moys MH (2006) Experimental study of oblique impacts with initial spin. Powder Technol 1:22–31
Ferrari F, Giacomini A, Thoeni K (2016) Qualitative rockfall hazard assessment: a comprehensive review of current practices. Rock Mech Rock Eng 49(7):2865–2922
Giani GP, Giacomini A, Migliazza M et al (2004) Experimental and theoretical studies to improve rock fall analysis and protection work design. Rock Mech Rock Eng 37(5):369–389
He SM (2010) Calculation of compact pressure of rock-fall on shield structures. Eng Mech 27(9):175–180
He SM, Yan SX, Deng Y, et al (2018) Impact protection of bridge piers against rockfall. Bull Eng Geol Environ 1–10
Hou TX, Yang XG, Huang C, Huang KX, Zhou JW (2015) A calculation method based on impulse theorem to determine impact force of rockfall on structure. Chin J Rock Mech Eng 34(s1):3116–3122
Hu J, Li SC, Shi SS et al (2018) Development and application of a model test system for rockfall disaster study on tunnel heading slope. Environ Earth Sci 78(14):391
Kawahara S, Muro T (2006) Effects of dry density and thickness of sandy soil on impact response due to rockfall. J Terrramech 43(3):329–340
Kobayashi Y, Harp EL, Kagawa T (1990) Simulation of rockfalls triggered by earthquakes. Rock Mech Rock Eng 23(1):1–20
Kohno M, Tsuchida A, Kitasako K, Ikezoe Y, Nishimura T (2016) Laboratory experiment and numerical analysis of rockfall impacts. J Soc Mater Sci Jpn 65(5):377–383
Labiouse V, Descoeudres F, Montain S (1996) Experimental study of rock sheds impacted by rock blocks. Struct Eng Int 6(3):171–176
Leine RI, Schweizer A, Christen M et al (2014) Simulation of rockfall trajectories with consideration of rock shape. Multibody SysDyn 32(2):241–271
Li LP, Lan HX (2015) Probabilistic modeling of rockfall trajectories: a review. Bull Eng Geol Environ 74(4):1163–1176
Lu Q, Zhou CF, Yu Y et al (2017) Experimental study on fragmentation effects of rockfall impact upon slope. Chin J Rock Mech Eng 36(s1):3359–3366
Oger L, Ammi M, Valance A et al (2005) Discrete element method studies of the collision of one rapid sphere on 2d and 3d packings. Eur Phys J E 17(4):467–476
Okura Y, Kitahara H, Sammori T, Kawanami A (2000) The effects of rockfall volume on runout distance. Eng Geol 58(2):109–124
Singh PK, Kainthola A, Panthee S et al (2016) Rockfall analysis along transportation corridors in high hill slopes. Environ Earth Sci 75(5):441
Thornton C (2009) A note on the effect of initial particle spin on the rebound behaviour of oblique particle impacts. Powder Technol 192(2):152–156
Xie L, Zheng XJ, Zhou YH (2003) A theoretical study of the distribution of the initial velocity of saltating sand particles by collision. Key Eng Mater 243–244:613–618
Zhang GC, Xiang X, Tang HM (2011) Field test and numerical calculation of restitution coefficient of rockfall collision. Chin J Rock Mech Eng 30(6):1266–1273
Zhang SL, Yang XG, Zhou JW (2018) A theoretical model for the estimation of maximum impact force from a rockfall based on contact theory. J Mt Sci 15(2):430–443
Zheng XJ, Zhu W, Xie L (2008) Exploration of probability distribution of velocities of saltating sand particles based on the stochastic particle-bed collisions. Sci China Ser G 51(8):976–985
Acknowledgements
This study was supported by the National Natural Science Foundation of China (Grant no. 11702124), Doctor Funding of Lanzhou University of Technology (Grant no. 04-061407). The authors would like to express their sincere appreciation to these supports.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Duan, S., Sun, J. Exploration of Probability Distribution of Velocities and Trajectory of Rolling Stone Based on Stochastic Rolling Stone Collision. Geotech Geol Eng 38, 3931–3940 (2020). https://doi.org/10.1007/s10706-020-01268-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10706-020-01268-8